- Виды, устройство и принцип действия
- Цифровые
- Униполярные
- Биполярные
- Омниполярные
- Аналоговые
- Обозрение процессов
- Свойства
- Примечания
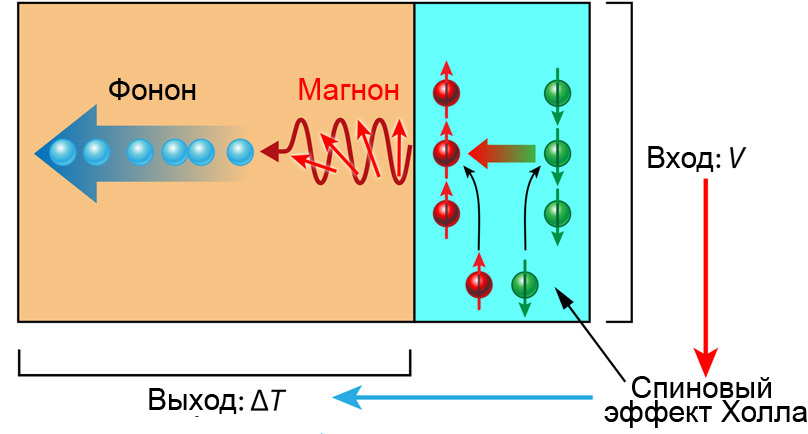
- Аномальный эффект Холла[ | код]
- Применение
- Достоинства и недостатки
- Формулы и расчёты
- Свойства
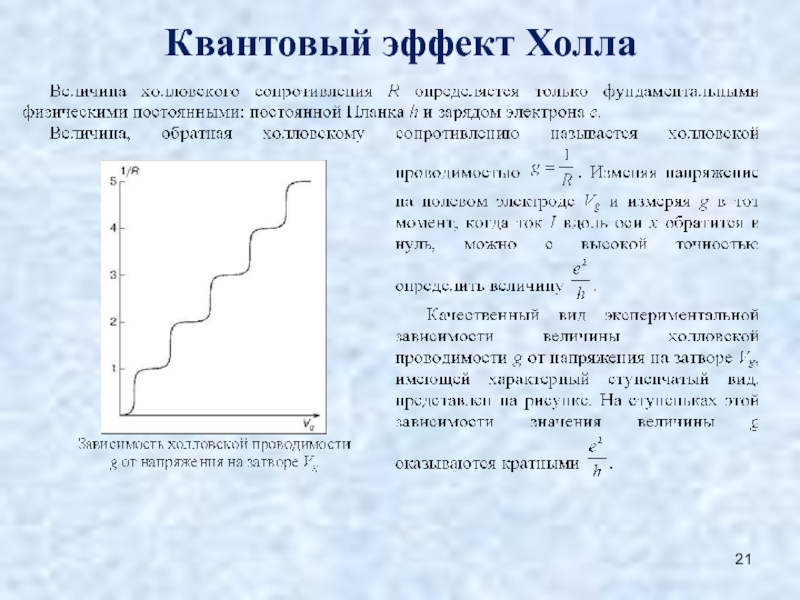
- Дробный квантовый эффект Холла
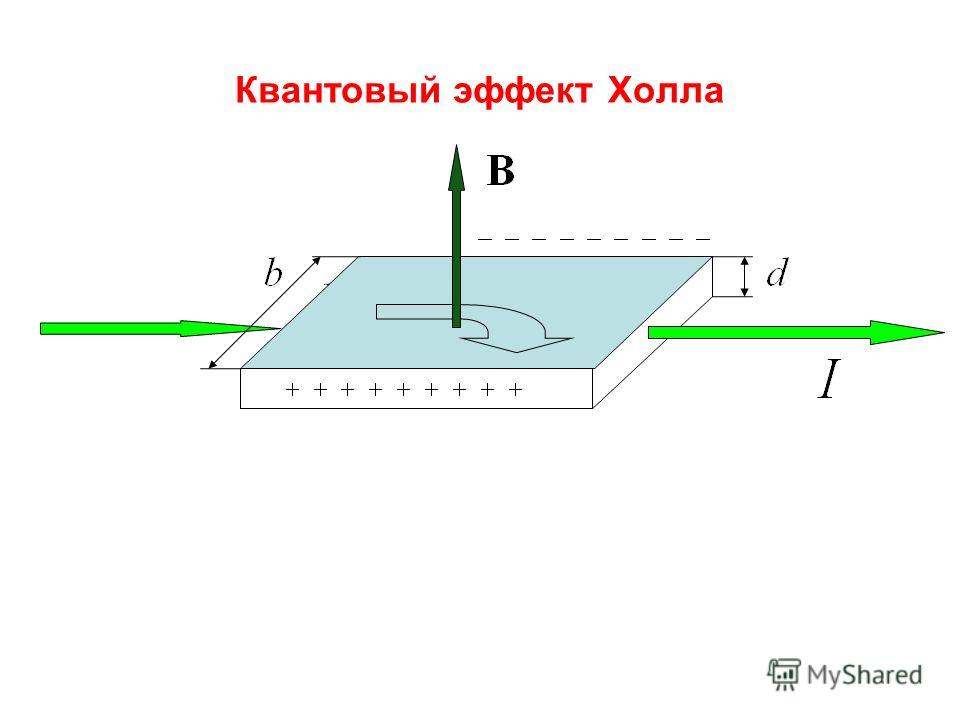
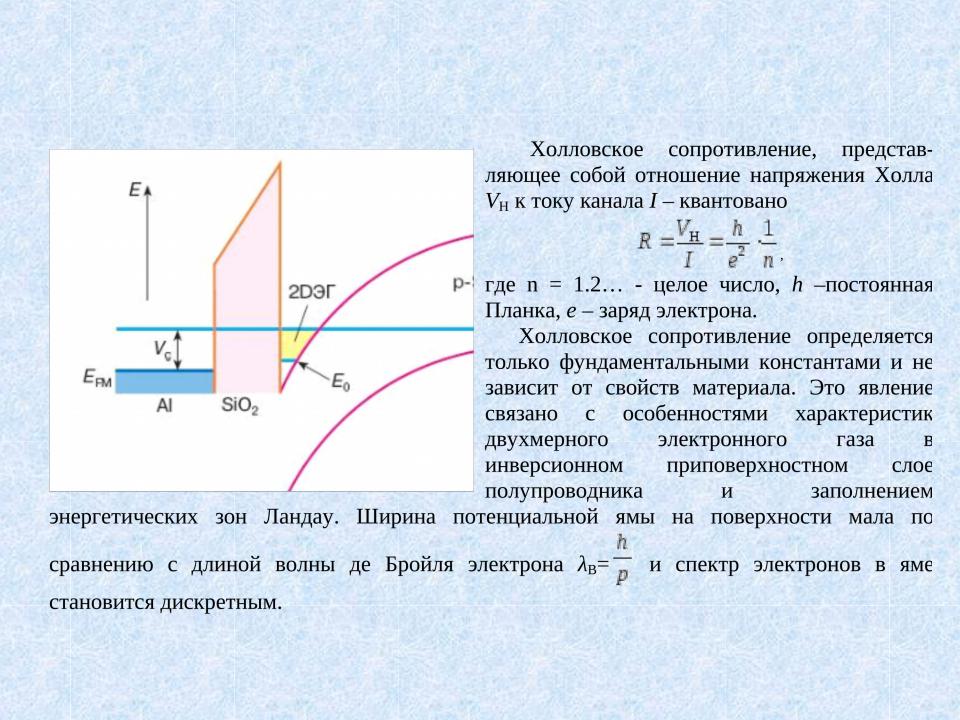
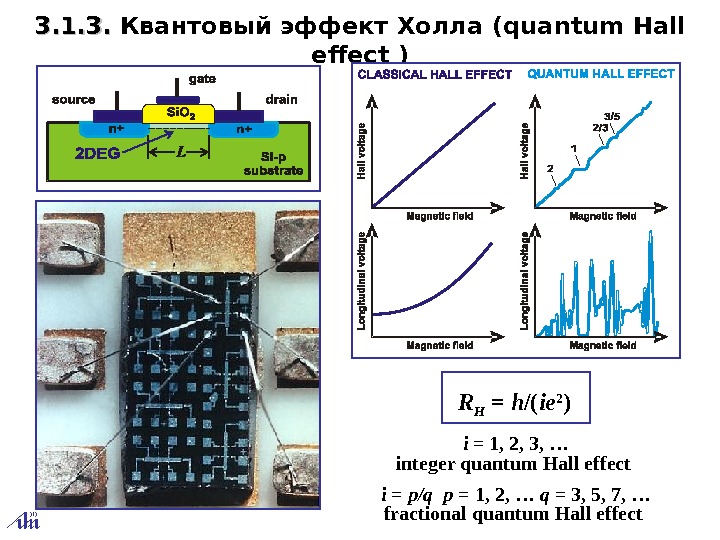
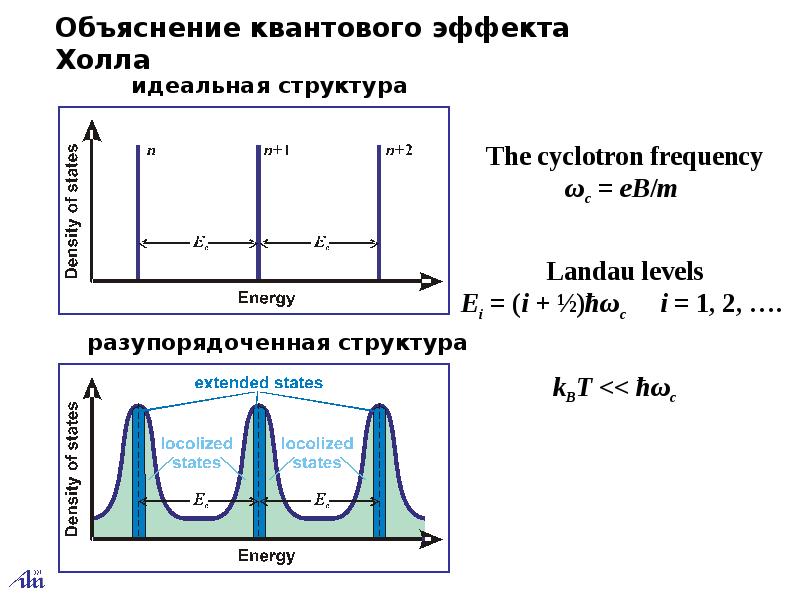
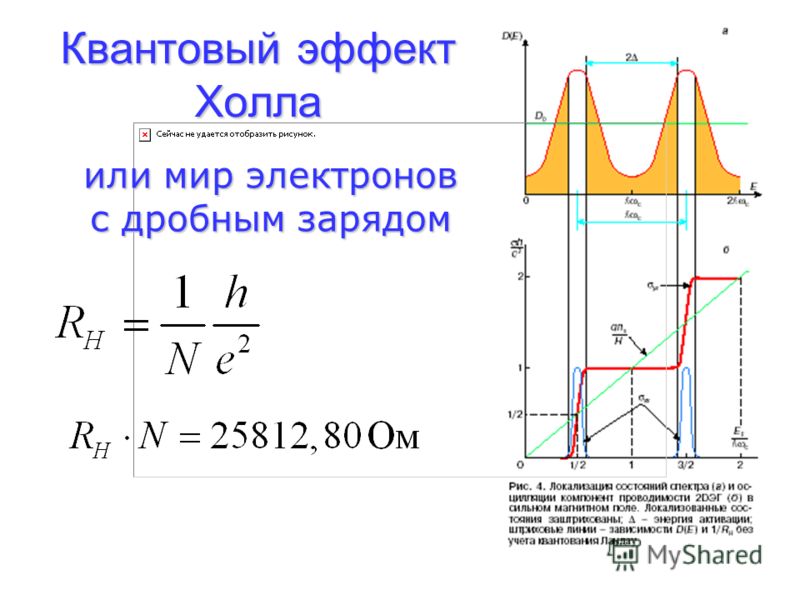
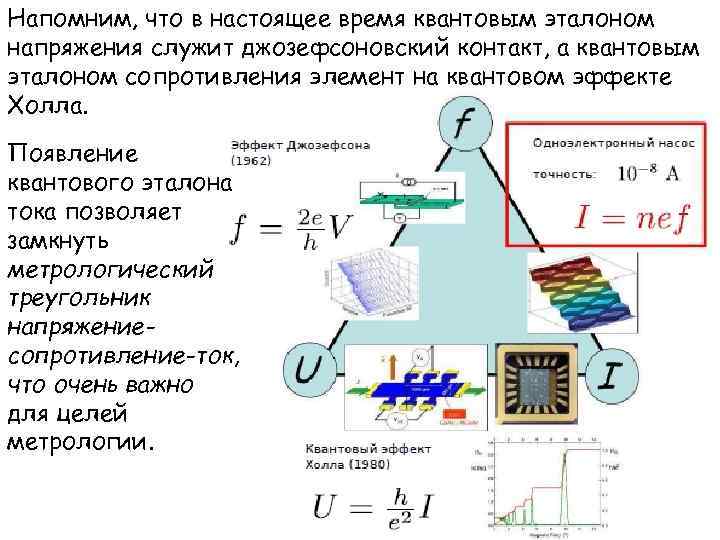
- Квантовый эффект Холла
- p-n переход
- p-n-p переход
- Расщепление основного уровня Ландау
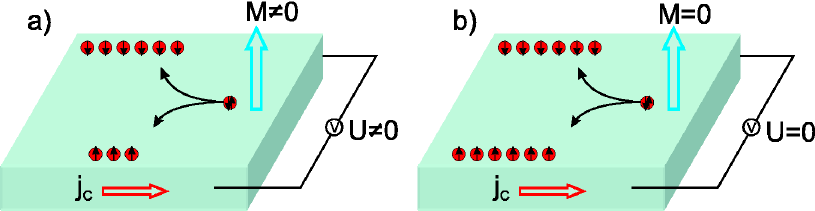
- Аномальный эффект Холла
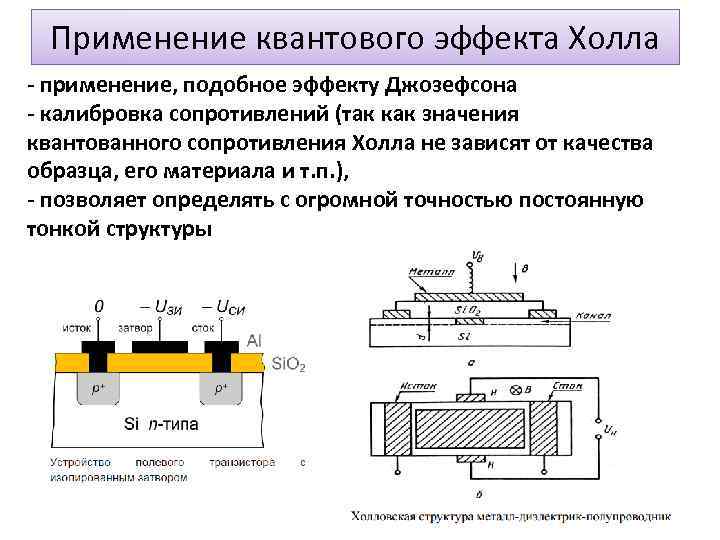
- Применение
- Что такое эффект Холла
- Аномальный эффект Холла
- Применение
- Применение
- Свойства[ | код]
- Что такое эффект Холла
- От Лоренца к Холлу
- Способы использования явления
- Уровни Ландау
Виды, устройство и принцип действия
Всего выделяют два вида датчиков на основе эффекта Холла. Первые – цифровые, вторые – аналоговые. Они значительно отличаются друг от друга в плане конструкции и принципа функционирования.
Цифровые
Цифровые регистры имеют два устойчивых положения: ноль или единица – то есть они срабатывают при определенной величине изменения магнитного поля. В основе таких датчиков лежит устройство под названием триггер Шмитта, которое имеет два устойчивых состояния: логический ноль и логическая единица.
Контроллеры подобного типа делятся на три вида:
- Униполярные.
- Биполярные.
- Омниполярные.
Каждый из этих видов далее будет подробно рассмотрен.
Униполярные
Контроллеры подобного вида работают только в том случае, если к ним прикладывается магнитное поле положительной полярности от южного полюса. Только при этом условии происходит срабатывание и отпускание контроллера.
Биполярные
Эти цифровые датчики работают под действием магнитного поля и южного, и северного полюса. Их особенность состоит в том, что срабатывают они под действием поля от южного полюса, а отпускаются под действием северного полюса.
Омниполярные
Уникальность этих контроллеров Холла состоит в том, что они могут включаться и выключаться под действием поля от любого полюса.
Аналоговые
В отличие от цифровых аналоговые датчики способны выдавать на выходе не два стабильных уровня сигнала, а бесконечное множество. Их принцип работы основан на преобразовании величины индукции поля в напряжение.
Конструкция этих устройств содержит элемент Холла (сам контроллер) и усилитель сигнала.
Обозрение процессов
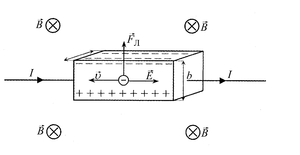
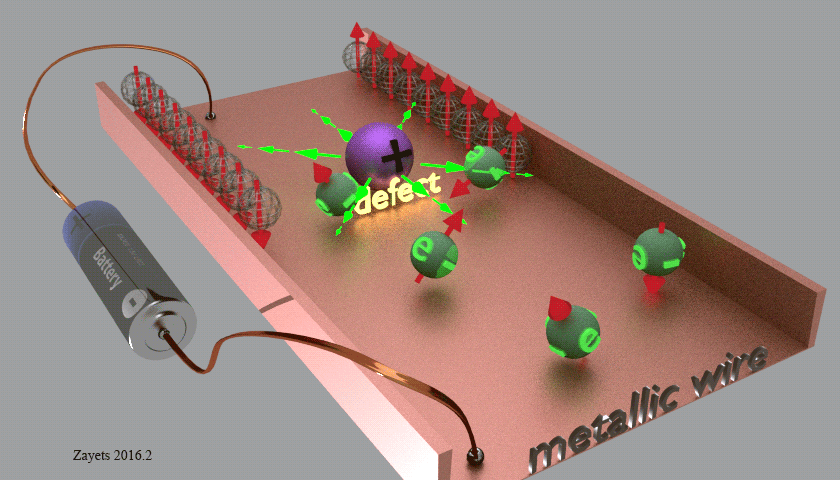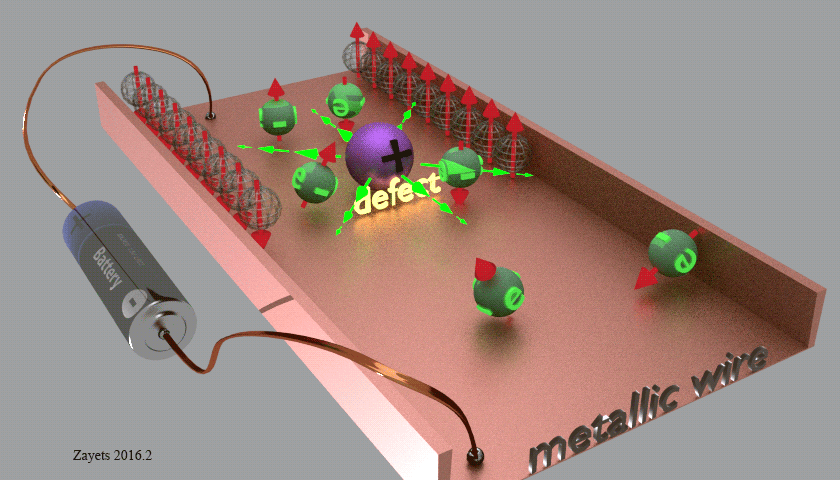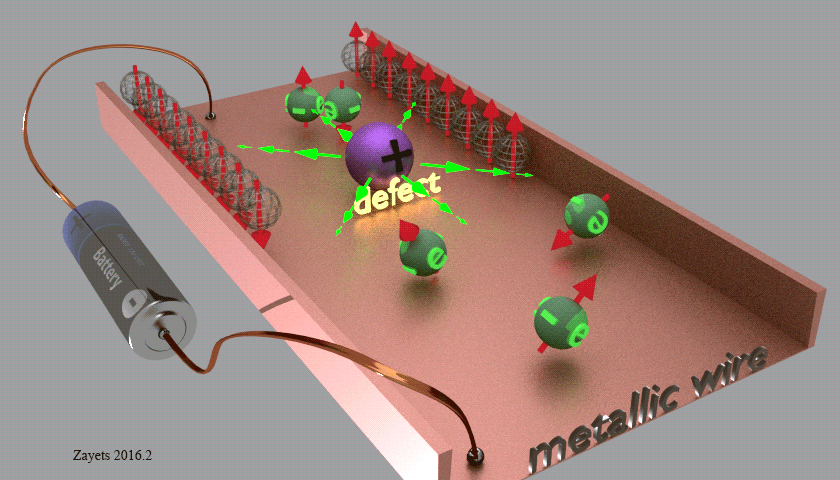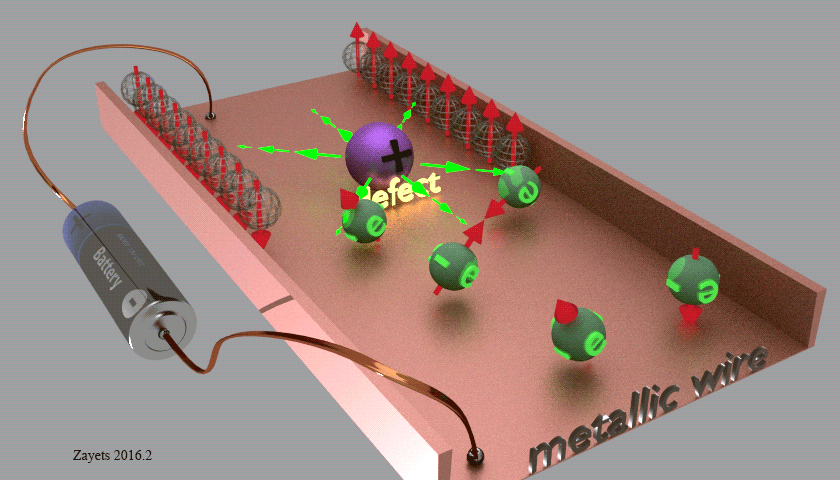
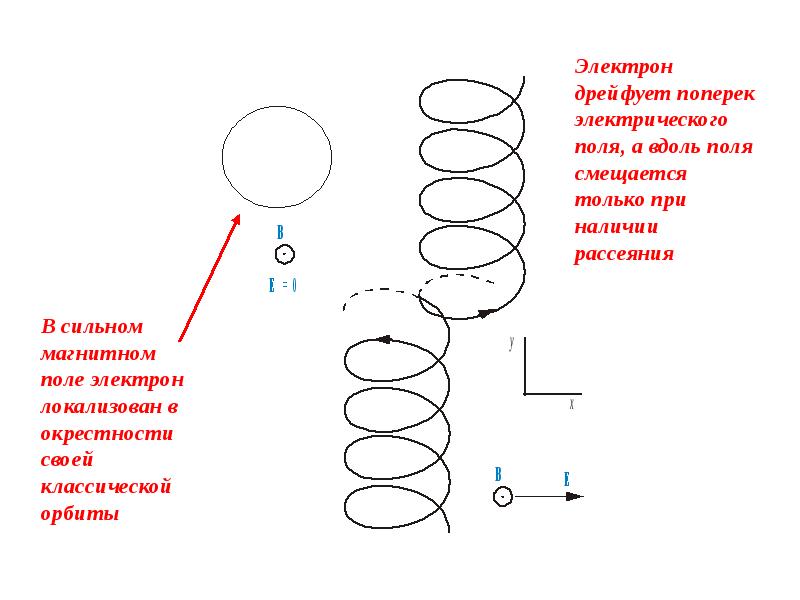
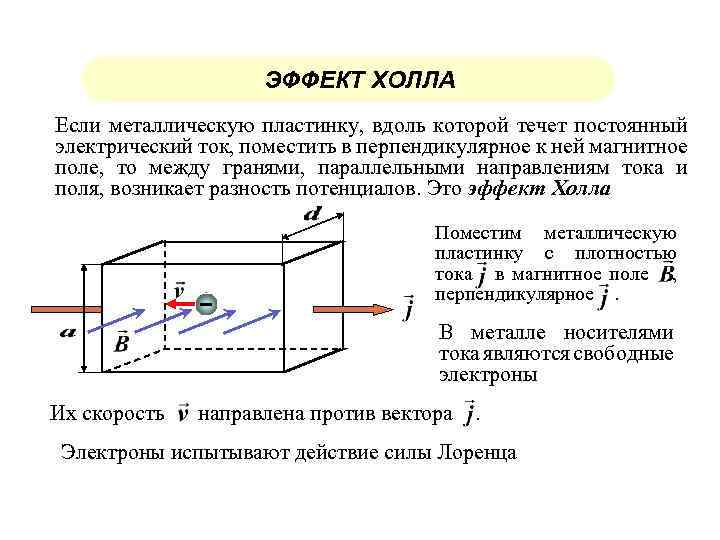
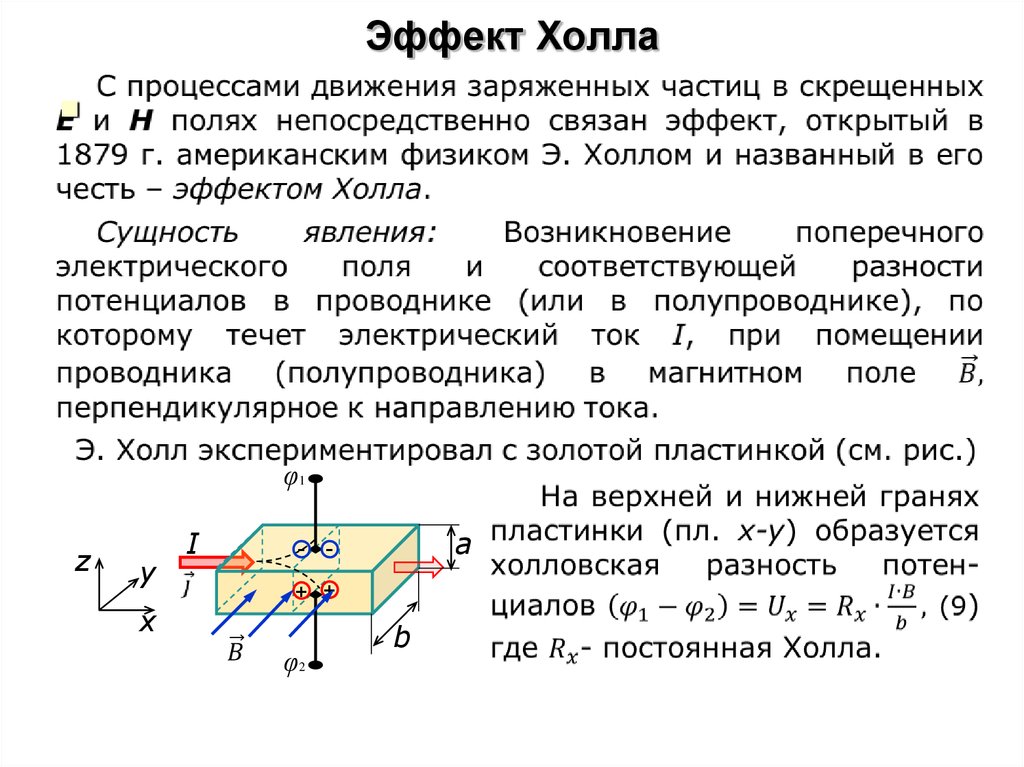
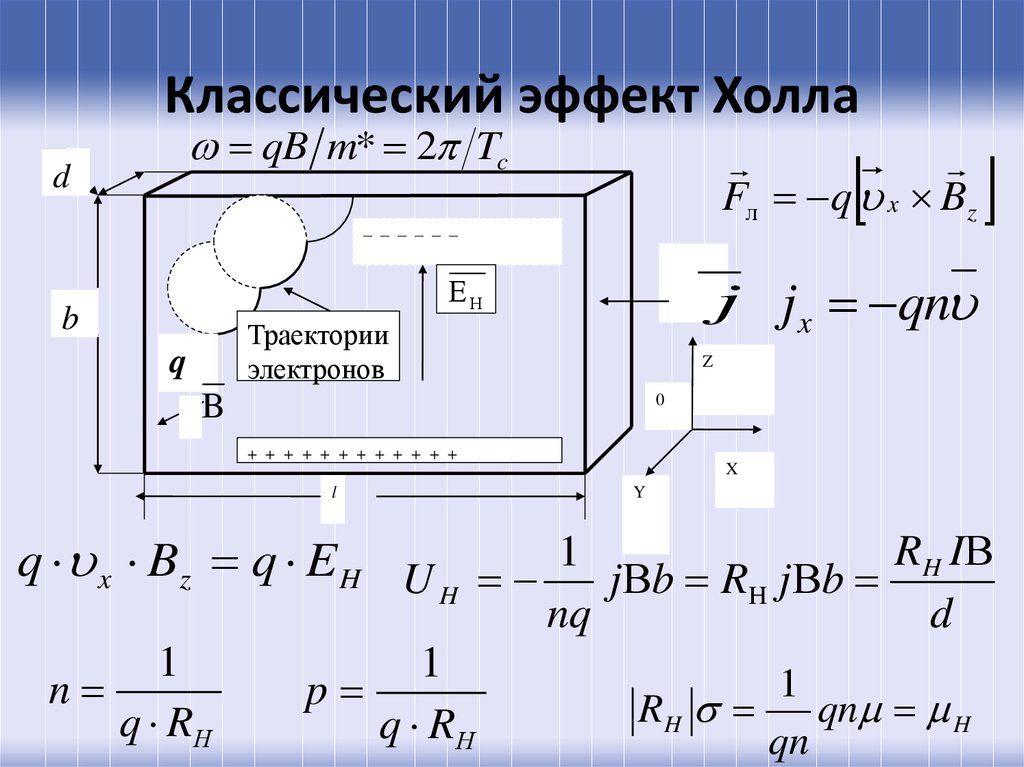
Рассмотрим эффект Холла с точки зрения протекания процессов в определенном проводнике на простейшем примере. Допустим, имеется брусок, который проводит электрический ток и при этом находится в м. п. со слабым потенциалом и под векторным напряжением электрического поля E. Находясь в таких условиях, носитель заряда (н. з.) будет отклоняться от м. п. в сторону одной из граней бруска либо противоположно по отношению к электрическому полю, либо вдоль от движения самого носителя. Показатель критерия малости в данном случае будет служить необходимостью, при которой н. з. не начинает движение по трансцендентной кривой плоскости.
В результате данного протекания процесса, сила Лоренца создаст условия, вызывающие накопление зарядов с отрицательным показателем, около одной грани бруска, а в противовес на другой грани будет накапливаться положительный заряд. Будет происходить накопление заряда до тех пор, пока образовавшееся поле не сможет компенсировать магнитный компонент составной силы Лоренца. Величина электронной скорости выражается при помощи плотности тока. RH, который в данном случае равен и пропорционален E1 и jB. Подобное явление называют константой Холла, или его коэффициентом.
Такое приближение носит знак постоянной Холла и зависит от н. з. Это дает возможность определять их тип для большого количества металлов. Например, определенные металлы в поле с высокими показателями силы носят положительный знак RH, а объяснение этому дают квантовая и полуклассическая теория твердых тел.
Свойства
В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через проводящий брусок в слабом магнитном поле с индукцией B{\displaystyle B} течёт электрический ток с плотностью j{\displaystyle j} под действием напряжённости E{\displaystyle E}. Магнитное поле будет отклонять носители заряда к одной из граней бруса от их движения вдоль или против электрического поля. При этом критерием малости будет служить условие, что при этом носители заряда не начнут двигаться по циклоиде.
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1{\displaystyle E_{1}} не скомпенсирует силу Лоренца:
- eE1=evB⇒E1=vB.{\displaystyle eE_{1}=evB\Rightarrow E_{1}=vB.}
- где e{\displaystyle e} — электрический заряд электрона.
Скорость электронов v{\displaystyle v} можно выразить через плотность тока j{\displaystyle j}:
- j=nev⇒v=jne,{\displaystyle j=nev\Rightarrow v={\frac {j}{ne}},}
- где n{\displaystyle n} — концентрация носителей заряда. Тогда
- E1=1nejB.{\displaystyle E_{1}={\frac {1}{ne}}jB.}
Коэффициент RH=1ne{\displaystyle R_{H}={\frac {1}{ne}}} пропорциональности между E1{\displaystyle E_{1}} и jB{\displaystyle jB} называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их знак заряда для большого числа металлов и полупроводников.
Несмотря на то, что носителями заряда в металлах являются электроны, имеющие отрицательный заряд, для некоторых металлов — например, таких, как свинец, цинк, железо, кобальт, вольфрам в достаточно сильном магнитном поле наблюдается положительный знак константы Холла RH{\displaystyle R_{H}}, что объясняется в полуклассической и квантовой теориях твёрдого тела.
Примечания
- ↑
- К. фон Клитцинг «Квантовый эффект Холла: Нобелевские лекции по физике — 1985 г.» УФН 150, 107 (1986).
- ↑
- ↑ Ando T., Fowler A. B. and Stern F. Electronic properties of two-dimensional systems Rev. Mod. Phys. 54, 437 (1982).
- Л. Д. Ландау, Е. М. Лифшиц «Теоретическая физика», в 10 т, т. 3 «Квантовая механика (нерелятивистская теория)», М., Физматлит, 2002, 808 с., ISBN 5-9221-0057-2 (т. 3), гл. 15 «Движение в магнитном поле», п. 112 «Движение в однородном магнитном поле», c. 554—559;
- Askerov, B. M. (англ.)русск.. Electron Transport Phenomena in Semiconductors, 5-е изд (англ.). — Singapore: World Scientific, 1994. — P. 416.
- В. К. Воронов, А. В. Подоплелов «Современная физика», учебное пособие, М., КомКнига, 2005, 512 с., ISBN 5-484-00058-0, гл. 4 «Полупрводники», п 4.7 «Квантовый эффект Холла», пп 4.7.4 «Целочисленный квантовый эффект Холла», с. 249—253;
- В. К. Воронов, А. В. Подоплелов «Современная физика», учебное пособие, М., КомКнига, 2005, 512 с., ISBN 5-484-00058-0, гл. 4 «Полупроводники», п 4.7 «Квантовый эффект Холла», пп 4.7.5 «Дробный квантовый эффект Холла», с. 253—259;
Аномальный эффект Холла[ | код]
Случай появления напряжения (электрического поля) в образце, перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля (то есть явление, полностью аналогичное эффекту Холла, но наблюдающееся без внешнего постоянного магнитного поля), называется аномальным эффектом Холла.
Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах с намагниченностью.
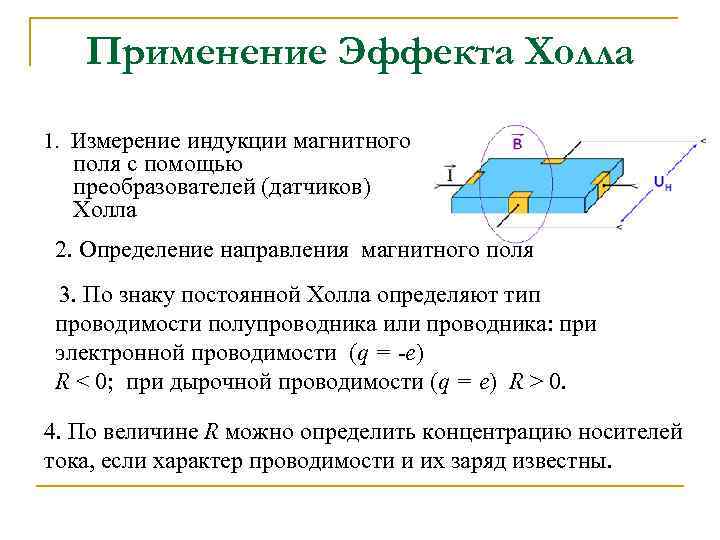
Применение
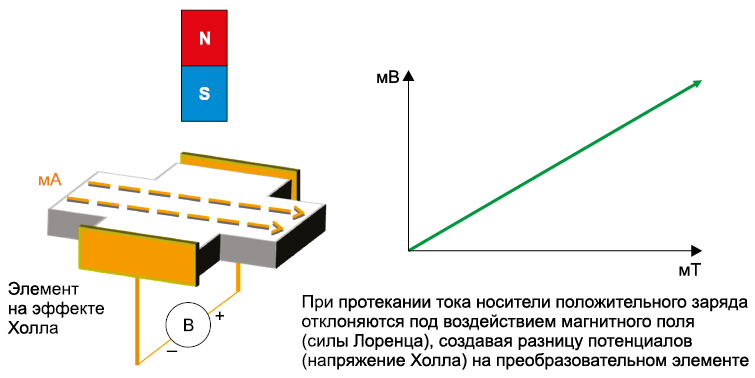
Датчик Холла, используемый для измерения силы тока в проводнике. В отличие от трансформатора тока, измеряет также и постоянный ток.
Эффект Холла позволяет определить концентрацию и подвижность носителей заряда, а в некоторых случаях − тип носителей заряда (электроны или дырки) в металле или полупроводнике, что делает его достаточно хорошим методом исследования свойств полупроводников (см. Метод ван дер Пау).
На основе эффекта Холла работают датчики Холла — приборы, измеряющие напряжённость магнитного поля. Датчики Холла получили очень большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя и выступают в роли датчика положения ротора (ДПР), который реализует обратную связь по положению ротора и выполняет ту же функцию, что и коллектор в коллекторном ДПТ.
Датчики Холла применяются:
- в системах электронного зажигания двигателей внутреннего сгорания;
- в приводах дисководов и двигателях вентиляторов компьютерной техники;
- в магнитометрах смартфонов в качестве физической основы работы электронного компаса;
- в электроизмерительных приборах (токоизмерительные клещи, пробники тока) для бесконтактного измерения силы тока (на фото).
- на основе эффекта Холла работают некоторые виды ионных реактивных двигателей
Достоинства и недостатки
Основное преимущество датчиков, созданных на основе данного эффекта, – изолированность цепей (измерения и токопроводящей). Кроме отмеченной выше хорошей защищенности от внешней среды, такое конструкторское решение обеспечивает отсутствие обратного влияния на основную электрическую схему. Подразумевается возможность оперативного изменения места измерения. Дополнительный плюс – минимальная мощность потребления.
Недостатком является ограниченная точность (1-2% в лучших образцах). Применение резистивного аналога в комплекте с дифференциальным усилителем позволяет улучшить результат с меньшими затратами. Однако в этом случае предполагаются монтаж контрольного компонента в рабочую цепь и сравнительное увеличение потребляемой мощности.
Также следует отметить ограниченный частотный диапазон датчиков Холла. Серийные модели функционируют корректно до 70-90 кГц. Более дорогие изделия широкополосной категории рассчитаны на применение до уровня 240-260 кГц. Нужно учитывать низкую чувствительность, которая вызывает затруднения при работе с малыми токами.
Формулы и расчёты
Закон полного тока
Так как в классическом определении эффект Холла – это перемещение зарядов под воздействием внешнего магнитного поля, можно сделать несколько выводов:
- образующееся в контрольных точках напряжение (Uх) будет прямо пропорционально току (I);
- аналогичная зависимость определена силовыми параметрами поля, которые выражают через вектор (В) магнитной индукции;
- существенное значение имеет размерность проводника.
Какой получится потенциал при определенных исходных параметрах? Ниже показан алгоритм преобразований с итоговой формулой для расчетов.
Для определения силы Лоренца (Fл) используют выражение:
Fл = q*v*B,
где:
- q – элементарный заряд;
- v – скорость его перемещения.
При подключении пластины по схеме основного эксперимента при постоянной силе тока разница потенциалов стабилизируется. После этого созданное электрическое поле будет воздействовать на заряды с определенной силой Fэ = q * E, где E – это соответствующая напряженность.
В этом состоянии Fл = Fэ, поэтому значение правых частей формул также будет равным: q*v*B = q * E. Следовательно E = v*B.
Плотность тока (j) определяется выражением:
j = q * v *n, где n – это число заряженных частиц в единице объема.
После преобразования выражения расчет для скорости подставляют в формулу напряженности:
E = (j/q*n) * B.
Разницу потенциалов несложно вычислить по напряженности и расстоянию (d) между контрольными точками (гранями пластины):
Uх = E * d = d * (j/q*n) * B = (1/q*n) * d * j * B.
Часть выражения (1/q*n) = R – это постоянная Холла. Она определяет обратную зависимость от суммарного заряда частиц.
Подставив коэффициент Холла в последнее выражение, можно записать итоговую формулу следующим образом:
Uх = R * d * j * B.
Свойства
В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через проводящий брусок в слабом магнитном поле с индукцией B{\displaystyle B} течёт электрический ток с плотностью j{\displaystyle j} под действием напряжённости E{\displaystyle E}. Магнитное поле будет отклонять носители заряда к одной из граней бруса от их движения вдоль или против электрического поля. При этом критерием малости будет служить условие, что при этом носители заряда не начнут двигаться по циклоиде.
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1{\displaystyle E_{1}} не скомпенсирует силу Лоренца:
- eE1=evB⇒E1=vB.{\displaystyle eE_{1}=evB\Rightarrow E_{1}=vB.}
- где e{\displaystyle e} — электрический заряд электрона.
Скорость электронов v{\displaystyle v} можно выразить через плотность тока j{\displaystyle j}:
- j=nev⇒v=jne,{\displaystyle j=nev\Rightarrow v={\frac {j}{ne}},}
- где n{\displaystyle n} — концентрация носителей заряда. Тогда
- E1=1nejB.{\displaystyle E_{1}={\frac {1}{ne}}jB.}
Коэффициент RH=1ne{\displaystyle R_{H}={\frac {1}{ne}}} пропорциональности между E1{\displaystyle E_{1}} и jB{\displaystyle jB} называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их знак заряда для большого числа металлов и полупроводников.
Несмотря на то, что носителями заряда в металлах являются электроны, имеющие отрицательный заряд, для некоторых металлов — например, таких, как свинец, цинк, железо, кобальт, вольфрам в достаточно сильном магнитном поле наблюдается положительный знак константы Холла RH{\displaystyle R_{H}}, что объясняется в полуклассической и квантовой теориях твёрдого тела.
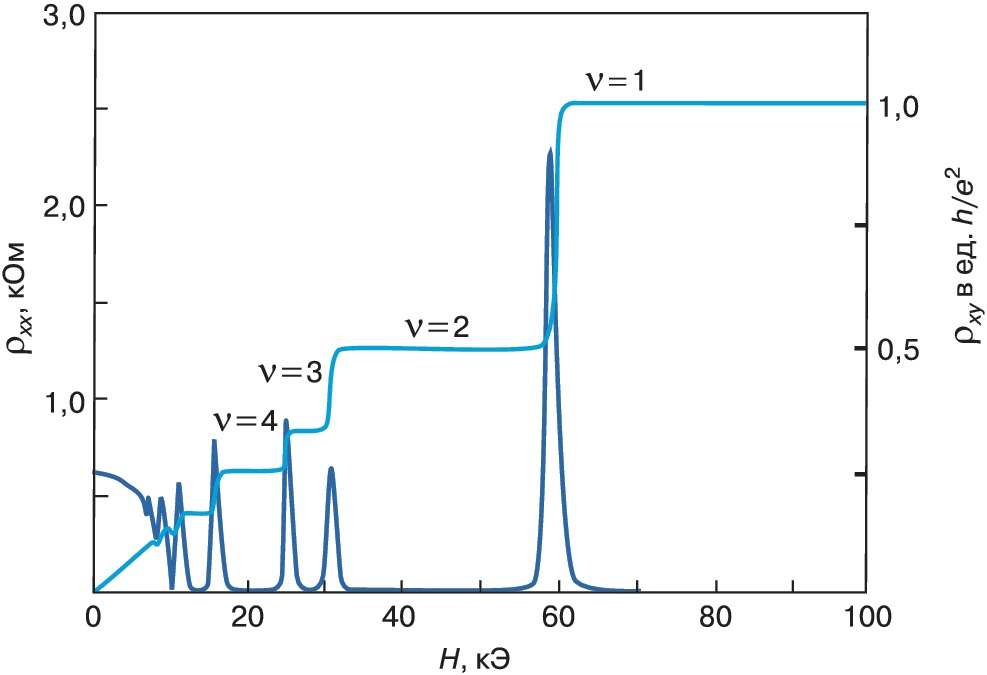
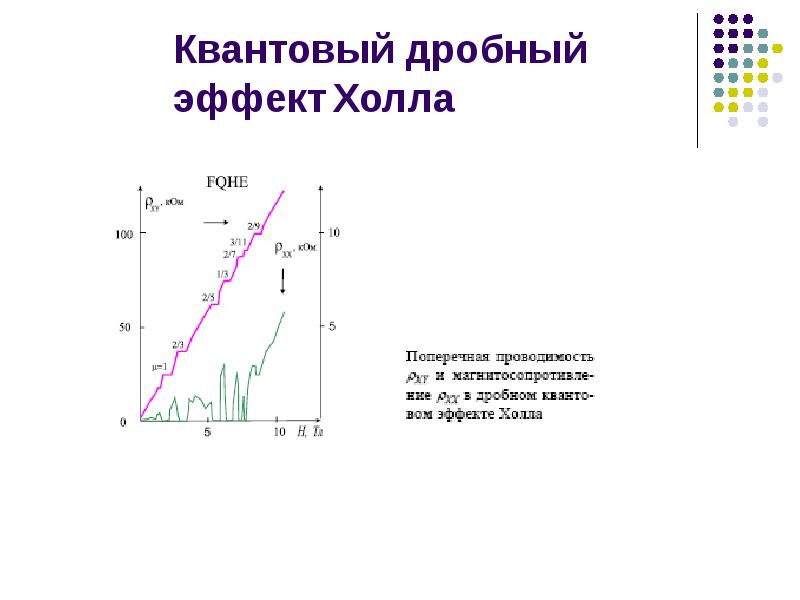
Дробный квантовый эффект Холла
Основная статья: Дробный квантовый эффект Холла
В 1982 году Даниэль Цуи (Daniel Tsui) и Хорст Штёрмер (Horst Störmer) заметили, что «плато» в холловском сопротивлении наблюдаются не только при целых значениях n, но и в существенно более сильных магнитных полях при n=1/3. В дальнейшем были обнаружены плато
электрического сопротивления и при других дробных значениях n, например при n=2/5, 3/7…
Природа дробного квантового эффекта Холла была объяснена Р. Лаффлином в 1983 году. В 1998 году Цуи, Штёрмер и Лаффлин получили Нобелевскую премию по физике за открытие и объяснение этого явления
Квантовый эффект Холла
Впервые необычный (англ. unconventional) квантовый эффект Холла наблюдали в работах, где было показано, что носители в графене действительно обладают нулевой эффективной массой, поскольку положения плато на зависимости недиагональной компоненты тензора проводимости соответствовали полуцелым значениям холловской проводимости ν=±(|n|+12){\displaystyle \nu =\pm (|n|+1/2)} в единицах 4e2h{\displaystyle 4e^{2}/h} (множитель 4 появляется из-за четырёхкратного вырождения энергии), то есть
- σxy=±4e2h(|n|+12){\displaystyle \sigma _{xy}=\pm {\frac {4e^{2}}{h}}\left(|n|+{\frac {1}{2}}\right)}.
Это квантование согласуется с теорией квантового эффекта Холла для дираковских безмассовых фермионов. Сравнение целочисленного квантового эффекта Холла в обычной двумерной системе и графене смотрите на рисунке 1. Здесь показаны уширенные уровни Ландау для электронов (выделение красным цветом) и для дырок (синий цвет). Если уровень Ферми находится между уровнями Ландау, то на зависимости холловской проводимости σxy{\displaystyle \sigma _{xy}} наблюдается ряд плато. Эта зависимость отличается от обычных двумерных систем (аналогом может служить двумерный электронный газ в кремнии, который является двухдолинным полупроводником в плоскостях эквивалентных {100}, то есть тоже обладает четырёхкратным вырождением уровней Ландау и холловские плато наблюдаются при ν=4|n|{\displaystyle \nu =4|n|}).
Квантовый эффект Холла (КЭХ) может использоваться как эталон сопротивления, потому что численное значение наблюдаемого в графене плато равное h2e2{\displaystyle h/2e^{2}} выполняется с хорошей точностью, хотя качество образцов уступает высокоподвижному ДЭГ в GaAs, и, соответственно, точности квантования. Преимущество КЭХ в графене в том, что он наблюдается при комнатной температуре (в магнитных полях свыше 20 Т). Основное ограничение на наблюдение КЭХ при комнатной температуре накладывает не само размытие распределения Ферми-Дирака, а рассеяние носителей на примесях, что приводит к уширению уровней Ландау.
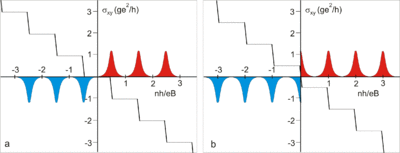
Рис. 1. a) Квантовый эффект Холла в обычной двумерной системе. b) Квантовый эффект Холла в графене. g=gsgv=4{\displaystyle g=g_{s}g_{v}=4} — вырождение спектра
p-n переход
Из-за отсутствия запрещённой зоны в графене в структурах с верхним затвором можно сформировать непрерывный p-n переход, когда напряжение на верхнем затворе позволяет инвертировать знак носителей, задаваемый обратным затвором в графене, где концентрация носителей никогда не обращается в ноль (кроме точки электронейтральности) и нет области лишённой носителей как в обычных p-n переходах. В таких структурах тоже можно наблюдать квантовый эффект Холла, но из-за неоднородности знака носителей значения холловских плато отличаются он приведённых выше. Для структуры с одним p-n переходом значения квантования холловской проводимости описываются формулой
- G=2e2h|ν′||ν||ν′|+|ν|,{\displaystyle G={\frac {2e^{2}}{h}}{\frac {|\nu ^{‘}||\nu |}{|\nu ^{‘}|+|\nu |}},}
где ν{\displaystyle \nu } и ν′{\displaystyle \nu ^{‘}} — факторы заполнения в n- и p- области соответственно (p-область находится под верхним затвором), которые могут принимать значения ±2,±6,±10{\displaystyle \pm 2,\pm 6,\pm 10} и т. д. Тогда плато в структурах с одним p-n переходом наблюдаются при значениях 1, 3/2, 3, 5/3 и т. д. Такие значения плато были наблюдены в эксперименте.
p-n-p переход
Для структуры с двумя p-n переходами соответствующие значения холловской проводимости равны
- G=e2h|ν′||ν|2|ν′|+|ν|=23,65,67,…(νν′).{\displaystyle G={\frac {e^{2}}{h}}{\frac {|\nu ^{‘}||\nu |}{2|\nu ^{‘}|+|\nu |}}={\frac {2}{3}},{\frac {6}{5}},{\frac {6}{7}},…(\nu \nu ^{‘}
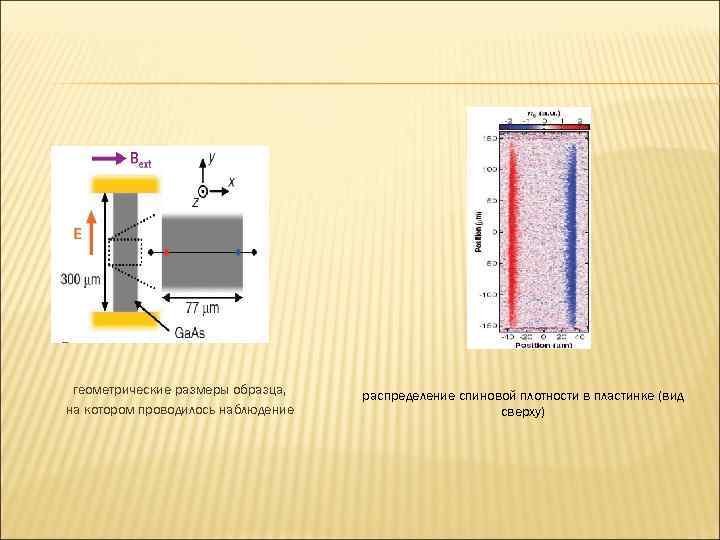
Расщепление основного уровня Ландау
В работе наблюдается спиновое расщепление релятивистских уровней Ландау и снятие четырёхкратного вырождения для наинизшего уровня Ландау вблизи точки электронейтральности. Для объяснения этого эффекта предложено несколько теорий.
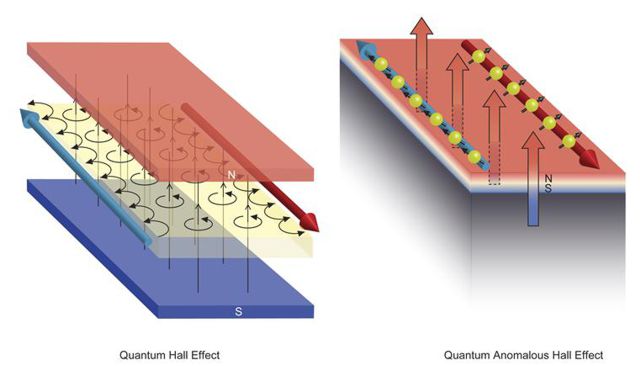
Аномальный эффект Холла
Случай появления напряжения (электрического поля) в образце, перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля (то есть явление, полностью аналогичное эффекту Холла, но наблюдающееся без внешнего постоянного магнитного поля), называется аномальным эффектом Холла.
Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах с намагниченностью.
Применение
Датчик Холла, используемый для измерения силы тока в проводнике. В отличие от трансформатора тока, измеряет также и постоянный ток.
Эффект Холла позволяет определить концентрацию и подвижность носителей заряда, а в некоторых случаях − тип носителей заряда (электроны или дырки) в металле или полупроводнике, что делает его достаточно хорошим методом исследования свойств полупроводников (см. Метод ван дер Пау).
На основе эффекта Холла работают датчики Холла — приборы, измеряющие напряжённость магнитного поля. Датчики Холла получили очень большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя и выступают в роли датчика положения ротора (ДПР), который реализует обратную связь по положению ротора и выполняет ту же функцию, что и коллектор в коллекторном ДПТ.
Датчики Холла применяются:
- в системах электронного зажигания двигателей внутреннего сгорания;
- в приводах дисководов и двигателях вентиляторов компьютерной техники;
- в магнитометрах смартфонов в качестве физической основы работы электронного компаса;
- в электроизмерительных приборах (токоизмерительные клещи, пробники тока) для бесконтактного измерения силы тока (на фото).
- на основе эффекта Холла работают некоторые виды ионных реактивных двигателей
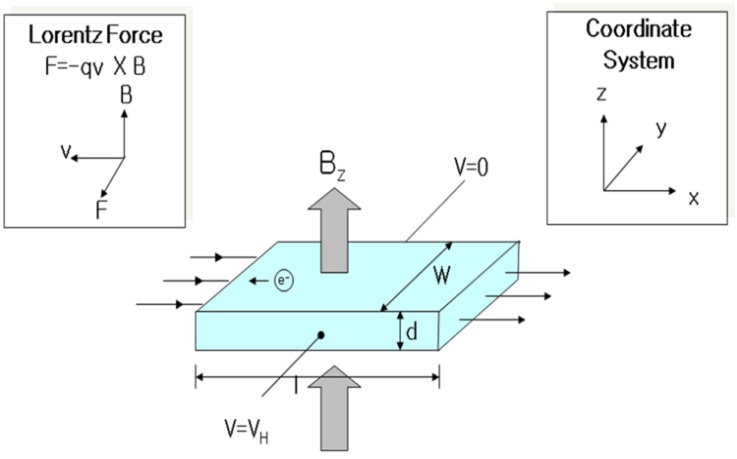
Что такое эффект Холла
Для повторения классического эксперимента не обязательно применение ценных металлов. Чтобы зарегистрировать возникновение разницы потенциалов, вполне достаточно чувствительности серийного лабораторного вольтметра. Сильный однородный магнитный поток обеспечить несложно, если подобрать подходящие изделия из неодимовых сплавов.
Если расположить проводник (пластину) в магнитном поле, как показано на рисунке, на торцах будет измеряться напряжение. Серией элементарных опытов можно обнаружить закономерность изменения показаний при увеличении (уменьшении) силы тока в рабочей цепи.
На этом принципе основано практическое применение эффекта Холла (ЭХ). По этой схеме выполняют измерение электрических параметров, не нарушая целостность токопроводящих цепей. Бесконтактный метод позволяет надежно изолировать датчик от неблагоприятных внешних воздействий. Такие методики помогают продлить долговечность оборудования, которое эксплуатируют в сложных условиях. В частности, подобные решения применяют в конструкциях автомобильной и авиационной техники.
Аномальный эффект Холла
Случай появления напряжения (электрического поля) в образце, перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля (то есть явление, полностью аналогичное эффекту Холла, но наблюдающееся без внешнего постоянного магнитного поля), называется аномальным эффектом Холла.
Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах с намагниченностью.
Применение
Датчик Холла, используемый для измерения силы тока в проводнике. В отличие от трансформатора тока, измеряет также и постоянный ток.
Эффект Холла позволяет определить концентрацию и подвижность носителей заряда, а в некоторых случаях − тип носителей заряда (электроны или дырки) в металле или полупроводнике, что делает его достаточно хорошим методом исследования свойств полупроводников (см. Метод ван дер Пау).
На основе эффекта Холла работают датчики Холла — приборы, измеряющие напряжённость магнитного поля. Датчики Холла получили очень большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя и выступают в роли датчика положения ротора (ДПР), который реализует обратную связь по положению ротора и выполняет ту же функцию, что и коллектор в коллекторном ДПТ.
Датчики Холла применяются:
- в системах электронного зажигания двигателей внутреннего сгорания;
- в приводах дисководов и двигателях вентиляторов компьютерной техники;
- в магнитометрах смартфонов в качестве физической основы работы электронного компаса;
- в электроизмерительных приборах (токоизмерительные клещи, пробники тока) для бесконтактного измерения силы тока (на фото).
- на основе эффекта Холла работают некоторые виды ионных реактивных двигателей
Применение
Датчик Холла, используемый для измерения силы тока в проводнике. В отличие от трансформатора тока, измеряет также и постоянный ток.
Эффект Холла позволяет определить концентрацию и подвижность носителей заряда, а в некоторых случаях − тип носителей заряда (электроны или дырки) в металле или полупроводнике, что делает его достаточно хорошим методом исследования свойств полупроводников (см. Метод ван дер Пау).
На основе эффекта Холла работают датчики Холла — приборы, измеряющие напряжённость магнитного поля. Датчики Холла получили очень большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя и выступают в роли датчика положения ротора (ДПР), который реализует обратную связь по положению ротора и выполняет ту же функцию, что и коллектор в коллекторном ДПТ.
Датчики Холла применяются:
- в системах электронного зажигания двигателей внутреннего сгорания;
- в приводах дисководов и двигателях вентиляторов компьютерной техники;
- в магнитометрах смартфонов в качестве физической основы работы электронного компаса;
- в электроизмерительных приборах (токоизмерительные клещи, пробники тока) для бесконтактного измерения силы тока (на фото).
- на основе эффекта Холла работают некоторые виды ионных реактивных двигателей
Свойства[ | код]
В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через проводящий брусок в слабом магнитном поле с индукцией B{\displaystyle B} течёт электрический ток с плотностью j{\displaystyle j} под действием напряжённости E{\displaystyle E}. Магнитное поле будет отклонять носители заряда к одной из граней бруса от их движения вдоль или против электрического поля. При этом критерием малости будет служить условие, что при этом носители заряда не начнут двигаться по циклоиде.
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1{\displaystyle E_{1}} не скомпенсирует силу Лоренца:
- eE1=evB⇒E1=vB.{\displaystyle eE_{1}=evB\Rightarrow E_{1}=vB.}
- где e{\displaystyle e} — электрический заряд электрона.
Скорость электронов v{\displaystyle v} можно выразить через плотность тока j{\displaystyle j}:
- j=nev⇒v=jne,{\displaystyle j=nev\Rightarrow v={\frac {j}{ne}},}
- где n{\displaystyle n} — концентрация носителей заряда. Тогда
- E1=1nejB.{\displaystyle E_{1}={\frac {1}{ne}}jB.}
Коэффициент RH=1ne{\displaystyle R_{H}={\frac {1}{ne}}} пропорциональности между E1{\displaystyle E_{1}} и jB{\displaystyle jB} называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определить знак их заряда для большого числа металлов и полупроводников.
Несмотря на то, что носителями заряда в металлах являются электроны, имеющие отрицательный заряд, для некоторых металлов — например, таких, как свинец, цинк, железо, кобальт, вольфрам в достаточно сильном магнитном поле наблюдается положительный знак константы Холла RH{\displaystyle R_{H}}, что объясняется в полуклассической и квантовой теориях твёрдого тела.
Что такое эффект Холла
Для повторения классического эксперимента не обязательно применение ценных металлов. Чтобы зарегистрировать возникновение разницы потенциалов, вполне достаточно чувствительности серийного лабораторного вольтметра. Сильный однородный магнитный поток обеспечить несложно, если подобрать подходящие изделия из неодимовых сплавов.
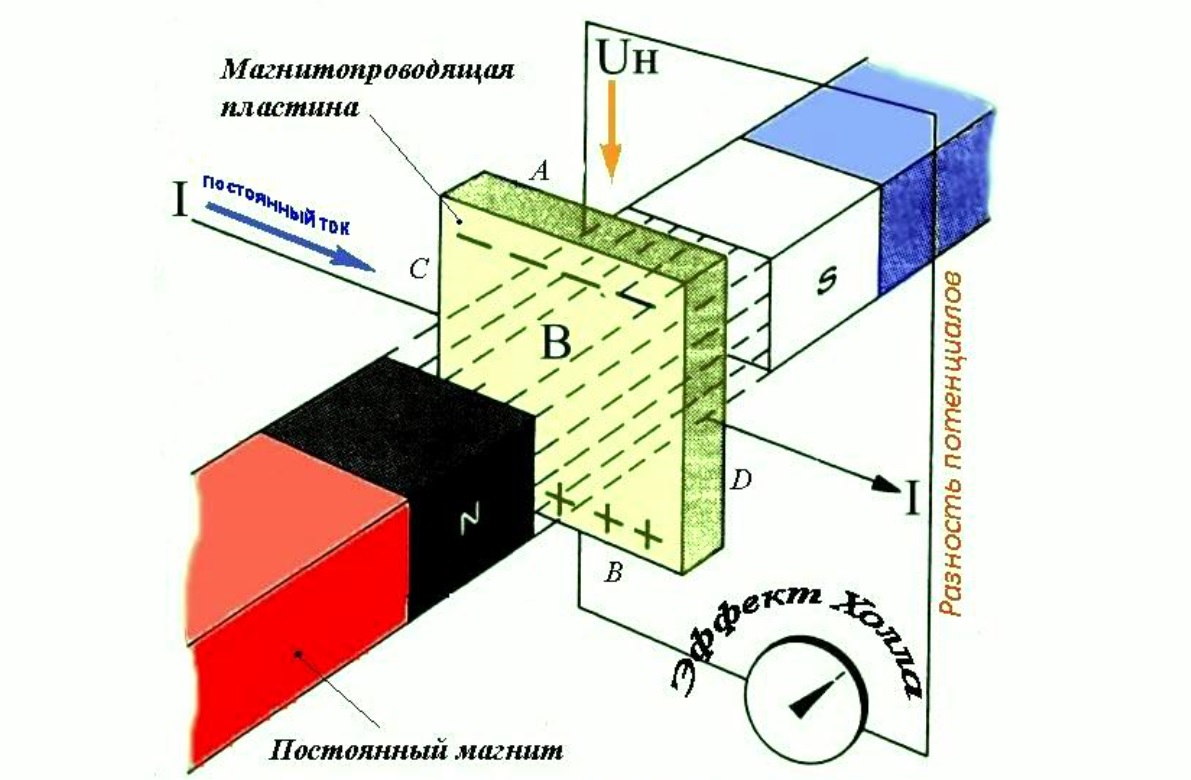 Что такое Холла эффект, можно выяснить с помощью наглядного эксперимента
Что такое Холла эффект, можно выяснить с помощью наглядного эксперимента
Если расположить проводник (пластину) в магнитном поле, как показано на рисунке, на торцах будет измеряться напряжение. Серией элементарных опытов можно обнаружить закономерность изменения показаний при увеличении (уменьшении) силы тока в рабочей цепи.
На этом принципе основано практическое применение эффекта Холла (ЭХ). По этой схеме выполняют измерение электрических параметров, не нарушая целостность токопроводящих цепей. Бесконтактный метод позволяет надежно изолировать датчик от неблагоприятных внешних воздействий. Такие методики помогают продлить долговечность оборудования, которое эксплуатируют в сложных условиях. В частности, подобные решения применяют в конструкциях автомобильной и авиационной техники.
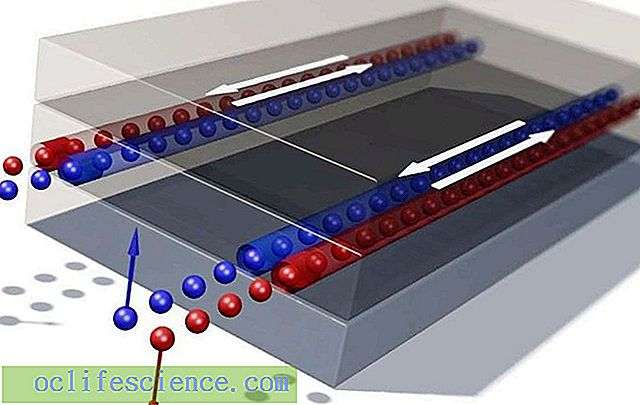
От Лоренца к Холлу
Для лучшего понимания физических процессов следует вспомнить базовые определения силы Лоренца. Они описывают воздействие на движущийся заряд магнитного поля. При перпендикулярном расположении силовых линий и вектора скорости электрон будет отклоняться вертикально вверх.
 Сила Лоренца и эффект Холла: пояснение основных зависимостей
Сила Лоренца и эффект Холла: пояснение основных зависимостей
На второй части рисунка показано, каким образом сила Лоренца воздействует на поток электронов. Их движение в определенном направлении обеспечивает подключенный источник постоянного тока. В соответствующих точках плоского проводника несложно измерить разницу потенциалов (Uх).
Для определения полярности потенциала пользуются известным правилом правой руки. Разместив ладонь в соответствии с направлением движения электронов, положением большого пальца определяют направление воздействия силы Лоренца. В рассматриваемом примере она перемещает отрицательные заряды на пластине вниз. Соответствующий знак «-» отмечен на картинке.
Способы использования явления
На основе эффекта Холла создаются устройства и приборы, обладающие нужными и часто уникальными свойствами
Эти приборы занимают важное место в измерительно-контрольной технике, автоматизации, радиотехнике и т. д
Приспособления, использующие в своей работе явление Холла, называются элементами Холла (датчиками).
Эти датчики дают возможность измерять силу магнитного поля, так как при неизменной величине тока электродвижущая сила прямо пропорциональна линиям магнитной индукции. Прямая зависимость этих величин для элементов Холла является неоспоримым преимуществом перед другими типами измерителей индукции, основанных на контроле магнетосопротивления.
Приборы Холла позволяют проводить измерения электрических и магнитных характеристик не только металлов, но и полупроводников. Из-за простоты своего действия, несложности в изготовлении, а также высокой точности и надёжности они широко применяются в различных отраслях науки и техники. Датчики используются для измерения силы, давления, углов, перемещения и других неэлектрических величин. Этот эффект используют и при изготовлении полупроводников для контроля подвижности носителей зарядов и подсчёта их концентрации.
Для этого используется формула эффекта Холла: V h = j*B*H / n*q = B*I / (q*n*α) = R*B*I/α,
из которой число носителей находится как N = (I*B) / (q*α* V h). Таким образом, можно определить не только количество носителей, но и также их тип (знак).
Элементы Холла применяются в автомобилестроении из-за их невысокой стоимости, точности показаний, надёжности и способности не зависеть от условий окружающей среды. Их используют в конструкции бесконтактных однополярных и биполярных прерывателей. Благодаря их миниатюрному исполнению электронные гаджеты можно автоматически включать или выключать экран при открытии или закрытии чехла с магнитом. Они помогают в GPS-навигации, улучшая геопозирование.
С каждым годом эффект Холла находит всё более новое применение. Свидетельством тому служит появление устройства виртуальной реальности — Google Card Board, в основе работы которого лежит взаимодействие магнита с датчиком Холла.
Уровни Ландау
| Графен |
| H^K=−iℏvFσ→⋅∇→{\displaystyle {\hat {H}}_{K}=-i\hbar v_{F}{\vec {\sigma }}\cdot {\vec {\nabla }}} |
| Физика графена Математическая формулировка … |
|
Основа Квантовая механика · Уравнение Дирака · Двумерный кристалл Нейтрино · (2+1)-мерная КЭД · Постоянная тонкой структуры · Фаза Берри · Углеродные нанотрубки |
|
Фундаментальные понятия История ·Зонная структура · Уравнение Дирака · Хиральность · Гексагональная решётка · Волновая функция · Точка электронейтральности · e-h лужи · Видимость графена · Фаза Берри · Двухслойный графен |
|
Получение и технология Получение графена · Механическое расщепление · Химические методы получения · Эпитаксия на металлы · Подвешенный графен · Верхний затвор · Перенос графена |
|
Применения Применение графенаГрафеновый полевой транзисторГрафеновые наноленты |
|
Транспортные свойства Электроны и дырки · Проводимость · Фононы· Парадокс Клейна · Линза Веселаго · 1/f · Дробовой шумСлучайный телеграфный сигнал · p — n переход · Ферми-жидкость |
|
Магнитное поле Магнетосопротивление · Осцилляции Шубникова — де Гааза · КЭХ · Спиновый квантовый эффект Холла · ДКЭХ · Осцилляции Вейса · Магнетоэкситоны · Сверхпроводимость · Слабая локализация · Эффект Ааронова — Бома |
|
Оптика графена Рамановское рассеяние света · α |
|
Известные учёные Андре Гейм · Константин Новосёлов · Филипп Ким · Михаил Кацнельсон |
| См. также: Портал:Физика |
Уровни Ландау в графене описываются уравнением Дирака для графена с учётом магнитного поля, которое можно записать в виде
- σ→⋅(iℏvF∇→+eA→c)ψ(x,y)=εψ(x,y){\displaystyle [{\vec {\sigma }}\cdot (i\hbar v_{F}{\vec {\nabla }}+e{\vec {A}}/c)]\psi (x,y)=\varepsilon \psi (x,y)}
где использована калибровка Ландау для векторного потенциала A→=(−By,){\displaystyle {\vec {A}}=(-By,0)}, двумерный градиент равен
∇→=(∂∂x,∂∂y){\displaystyle {\vec {\nabla }}=({\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}})}, а вектор σ→{\displaystyle {\vec {\sigma }}} составлен из матриц Паули (σ1,σ2){\displaystyle (\sigma _{1},\sigma _{2})}. В матричном виде уравнение запишется в виде
- (−iℏv∂∂x−ℏv∂∂y+eBy−iℏvF∂∂x+ℏv∂∂y+eBy)ψ(x,y)=εψ(x,y).{\displaystyle {\begin{pmatrix}0&-i\hbar v{\frac {\partial }{\partial x}}-\hbar v{\frac {\partial }{\partial y}}+eBy\\-i\hbar v_{F}{\frac {\partial }{\partial x}}+\hbar v{\frac {\partial }{\partial y}}+eBy&0\end{pmatrix}}\psi (x,y)=\varepsilon \psi (x,y).}
Здесь можно легко разделить переменные и в итоге прийти к спектру для релятивистских уровней Ландау
- εn=±ℏωc~n=±ℏvF2eB2nc,{\displaystyle \varepsilon _{n}=\pm \hbar {\tilde {\omega _{c}}}{\sqrt {n}}=\pm {\sqrt {\hbar v_{F}^{2}eB2n/c}},}
где n=,1,2,…{\displaystyle n=0,\,1,\,2,…}, «циклотронная частота» равна ωc~=2vFlB{\displaystyle {\tilde {\omega _{c}}}={\sqrt {2}}{\frac {v_{F}}{l_{B}}}}, магнитная длина lB=ℏceB.{\displaystyle l_{B}={\sqrt {\frac {\hbar c}{eB}}}.}