Расчет величины индукции магнитных полей по формуле и определение индуктивности

Содержание

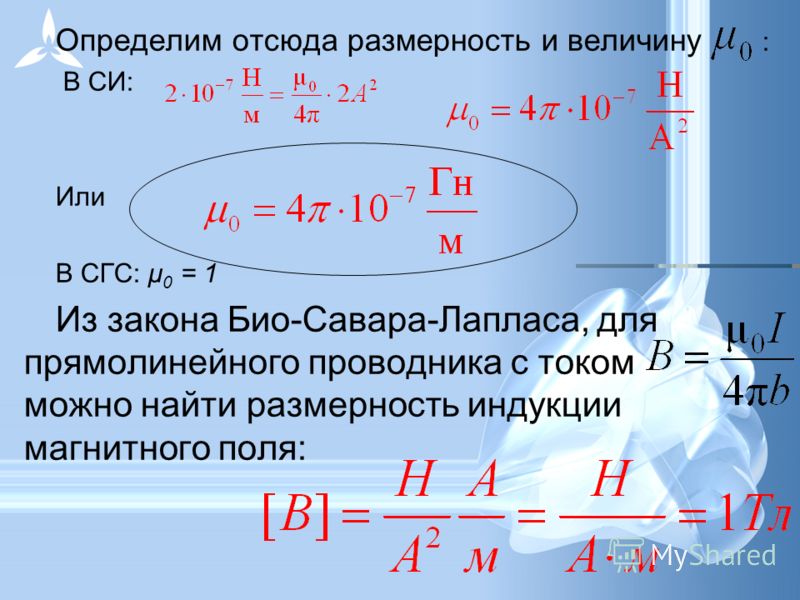
Способы расчёта
Через силу тока
Соленоид конечной длины
Катушка с тороидальным сердечником
Длинный проводник
Одновитковой контур и катушка
Что такое индуктивность
ЭДС индукции
Применение катушек в технике
Соленоид
ÐÐ°Ð³Ð½Ð¸ÑÐ½Ð¾Ðµ Ð¿Ð¾Ð»Ðµ
«Катушка ниток»
Основные формулы для вычисления вектора МИ
Закон Био-Савара-Лапласа
Принцип суперпозиции
Теорема о циркуляции
Магнитный поток
ÐÐ¸Ð´Ñ ÐºÐ°ÑÑÑÐµÐº
Основные уравнения
В магнитостатике
В общем случае
Вариометр
ÐÑÑÐ¾ÑÐ¸Ñ
Общие сведения
Свойства магнетизма
Линии магнитной индукции
Материал сердечника
Современные магнитные материалы
Как найти активную, реактивную и полную мощность

Способы расчёта

Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.

Через силу тока

Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:

L — индуктивность контура (в генри);
Ф — величина магнитного потока, измеряемого в веберах;
I — сила тока в катушке (в амперах).

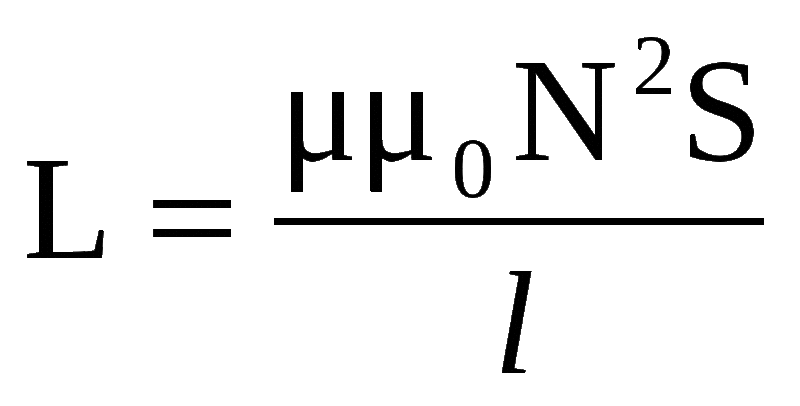
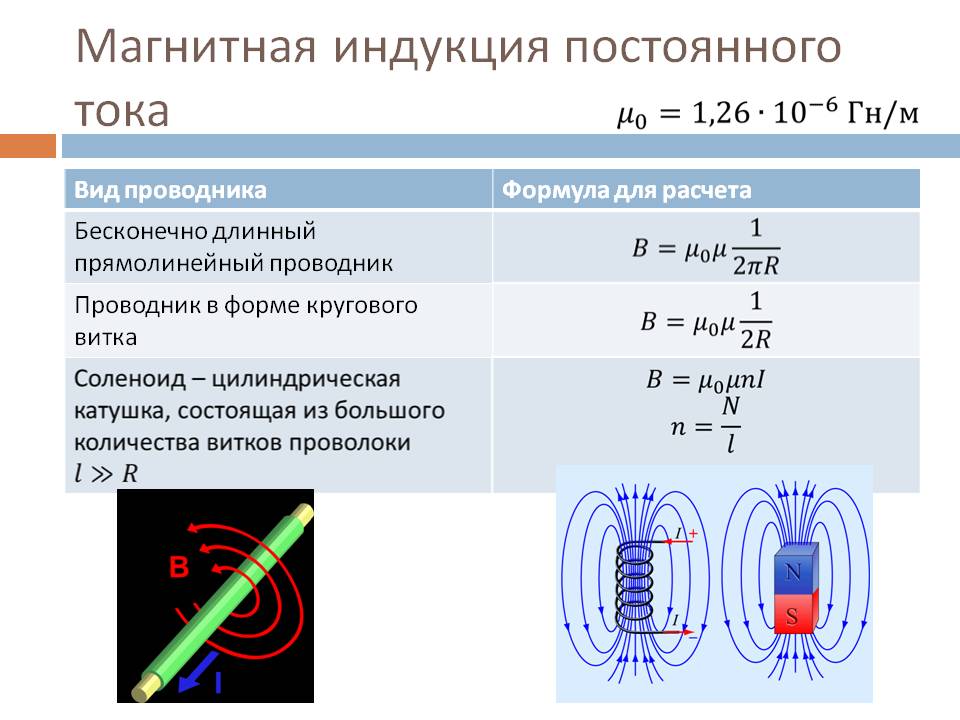
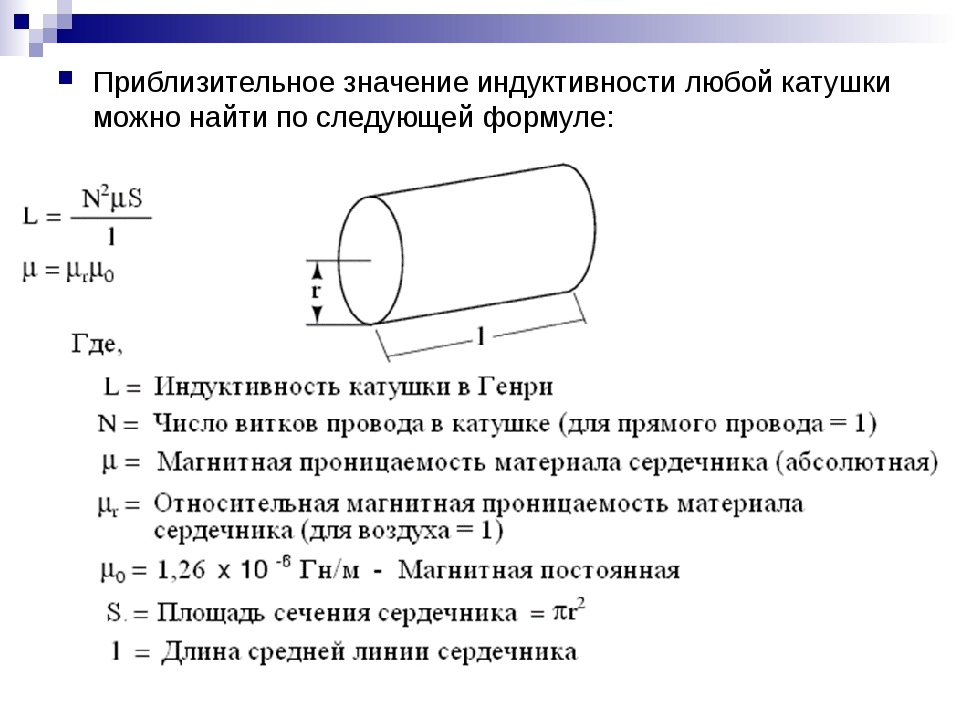
Соленоид конечной длины

Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:

µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
N — количество витков в катушке;
S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
l — длина соленоида в метрах.

Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:

W — энергия магнитного потока, измеряемая в джоулях;
I — сила тока в амперах.

Катушка с тороидальным сердечником

В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:

N — число витков катушки;
µ — относительная магнитная проницаемость;
µ0 — магнитная постоянная;
S — площадь сечения сердечника;
π — математическая постоянная, равная 3,14;
r — средний радиус тора.

Длинный проводник

Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:

l — длина проводника в метрах;
r — радиус сечения провода, измеряемый в метрах;
µ0 — магнитная постоянная;
µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
π — число Пи;
ln — обозначение логарифма.

Одновитковой контур и катушка

Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:

L=Ф/I.

Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.

Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:

L=L1∙N2.

Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.

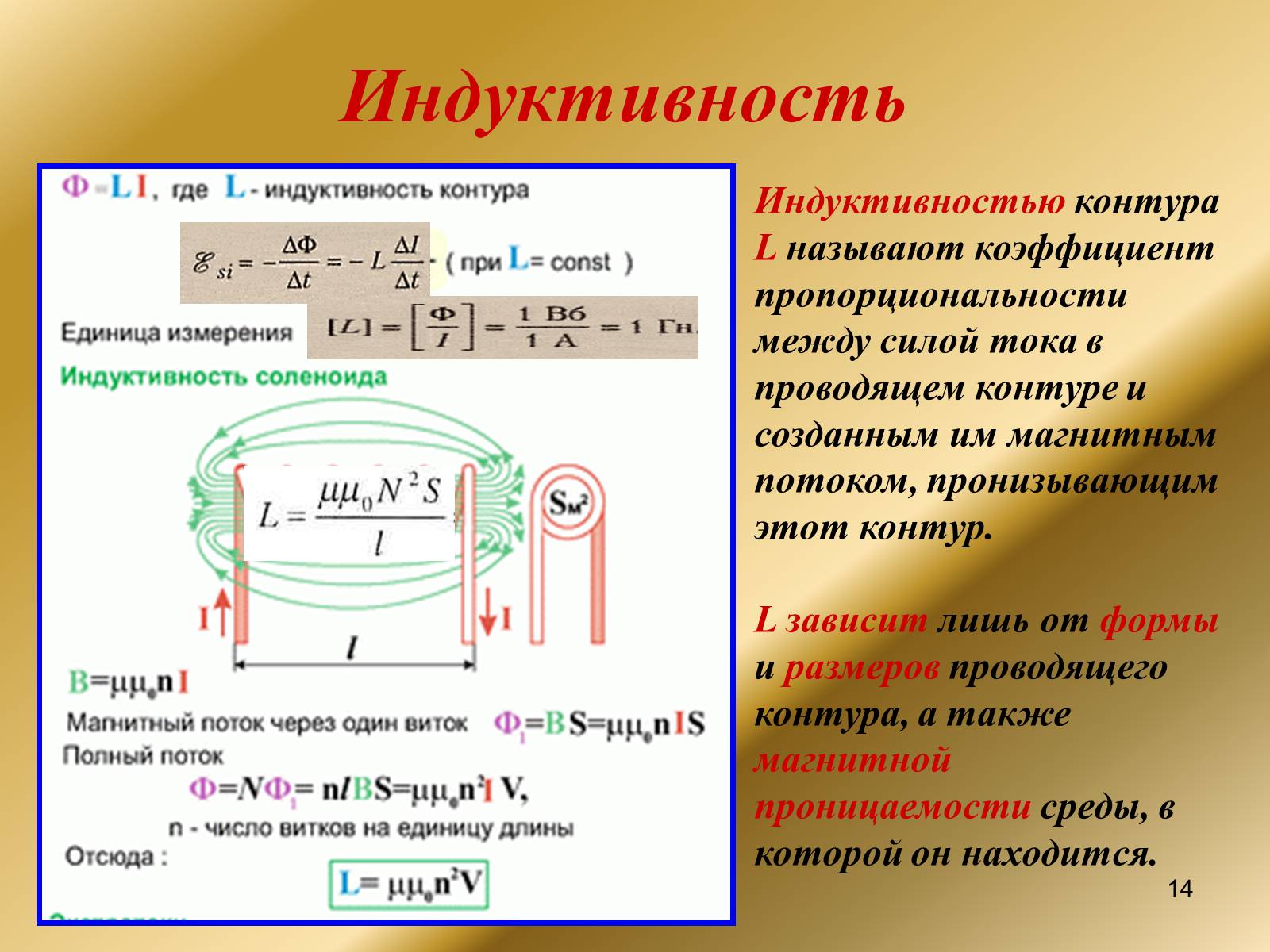
Что такое индуктивность

Этим термином обозначают зависимость, которая устанавливается между силой тока в проводнике (I) и созданным магнитным потоком (Ф):

L = Ф/ I.

С учетом базового определения несложно понять зависимость индуктивности от свойств окружающей среды, оказывающей влияние на распределение силовых линий. Определенное значение имеют размеры и конфигурация проводящего элемента.

Индуктивность подобна механической инерции. Только в данном случае речь идет о действиях с электрическими величинами. Этим коэффициентом характеризуют способность рассматриваемого компонента противодействовать изменению проходящего через него тока.

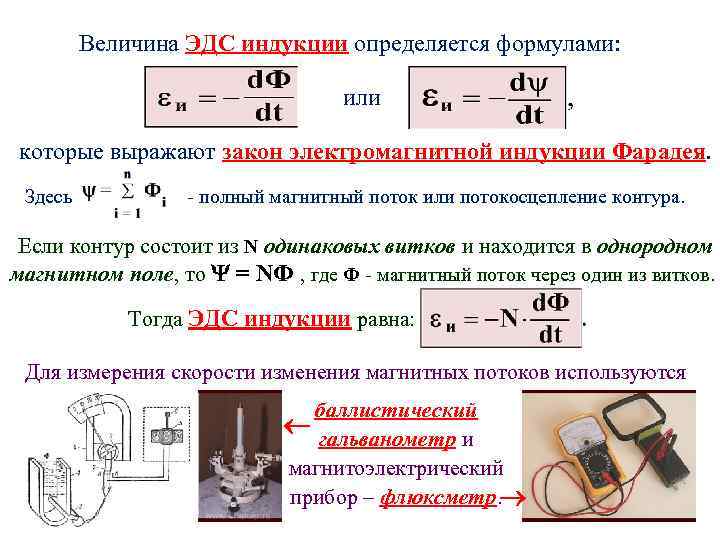
ЭДС индукции

Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.

Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.

Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.

Применение катушек в технике

Явление электромагнитной индукции известно уже давно и широко применяется в технике. Примеры использования:

сглаживание пульсаций и помех, накопление энергии;
создание магнитных полей в различных устройствах;
фильтры цепей обратной связи;
создание колебательных контуров;
трансформаторы (устройство из двух катушек, связанных индуктивно);
силовая электротехника использует для ограничения тока при к. з. на ЛЭП (катушки индуктивности, называются реакторами);
ограничение тока в сварочных аппаратах — катушки индуктивности делают его работу стабильнее, уменьшая дугу, что позволяет получить ровный сварочный шов, имеющий наибольшую прочность;
применение катушек в качестве электромагнитов различных исполнительных механизмов;
обмотки электромагнитных реле;
индукционные печи;
установление качества железных руд, исследование горных пород при помощи определения магнитной проницаемости минералов.

Соленоид

Соленоид отличается от обычной катушки по двум признакам:

Длина обмотки превышает диаметр в несколько раз;
Толщина обмотки меньше диаметра катушки также в несколько раз.

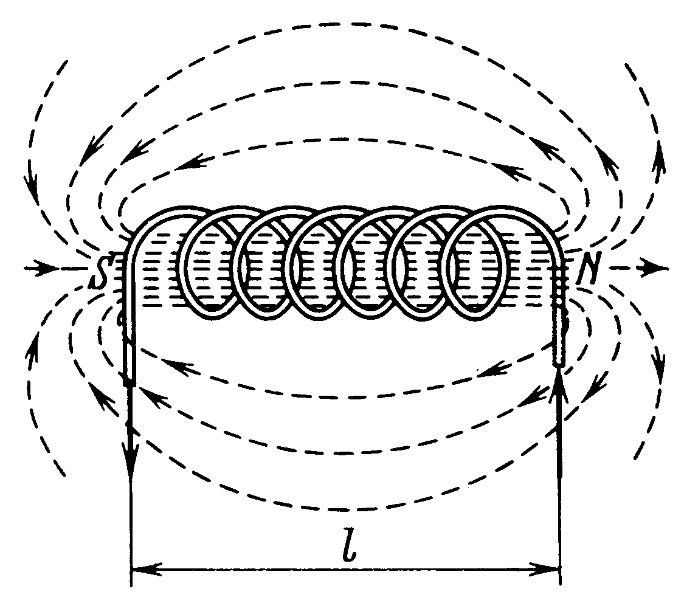Соленоидальный тип катушки

Параметры соленоида можно узнать из такого выражения:

L=µ0N2S/l,

где:

µ0 – магнитная постоянная;
N – количество витков;
S – площадь поперечного сечения обмотки;
l – длина обмотки.

Важно! Приведенное выражение справедливо для соленоида без сердечника. В противном случае необходимо дополнительно внести множитель µ, который равен магнитной проницаемости сердечника

Чем большую магнитную проницаемость будет иметь сердечник, тем больше увеличится итоговое значение.

ÐÐ°Ð³Ð½Ð¸ÑÐ½Ð¾Ðµ Ð¿Ð¾Ð»Ðµ

«Катушка ниток»

Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.

Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:

I = U : R,

где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.

Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка – источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.

Катушку можно разделить на два вида:

С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.

Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:

L = 10µ0ΠN2R2 : 9R + 10l.

А вот уже для многослойной другая формула:

L= µ0N2R2 :2Π(6R + 9l + 10w).

Основные выводы, связанные с работой катушек:

На цилиндрическом феррите самая большая индуктивность возникает в середине.
Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
Индуктивность тем меньше, чем меньше количество витков.
В тороидальном сердечнике расстояние между витками не играет роли катушки.
Значение индуктивности зависит от «витков в квадрате».
Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.

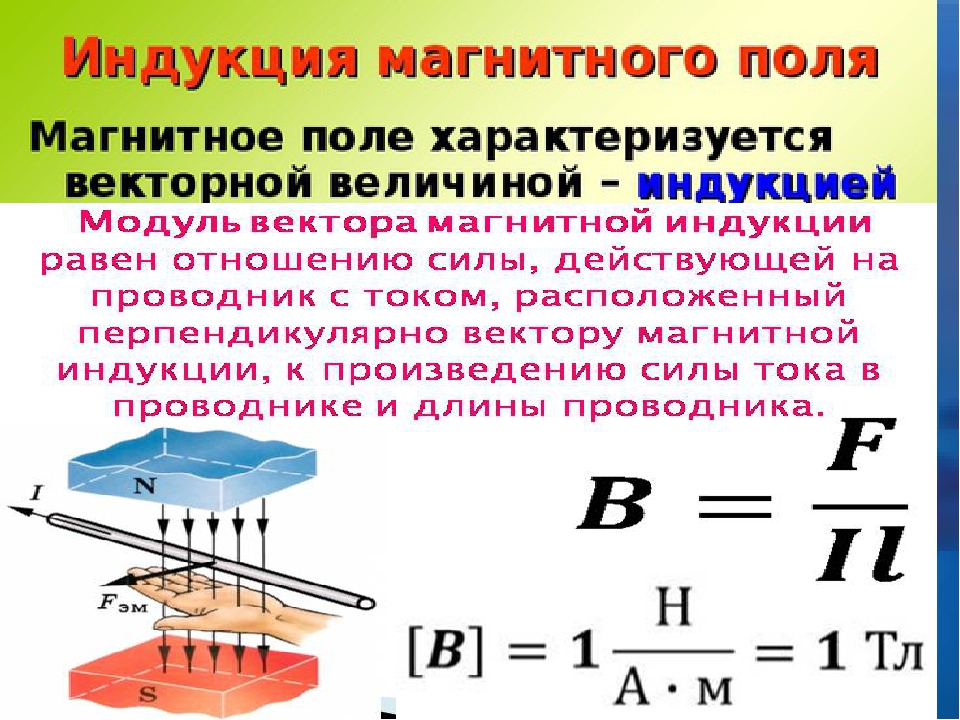
Основные формулы для вычисления вектора МИ

Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.

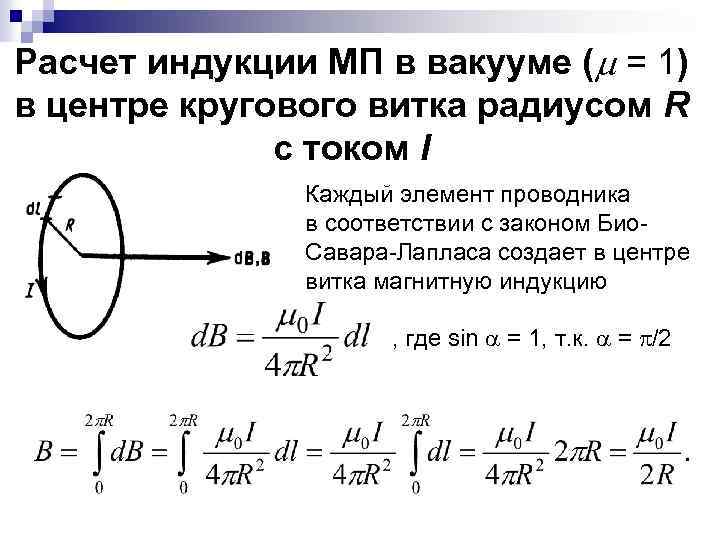
Закон Био-Савара-Лапласа

Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.

Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.

Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB

dB = µ0 *I*dl*sin α /4*π*r2,

где

dB – магнитная индукция, Тл;
µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
I – сила тока, А;
dl – отрезок проводника, м;
r – расстояние до точки нахождения магнитной индукции, м;
α – угол, образованный r и вектором dl.

Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме

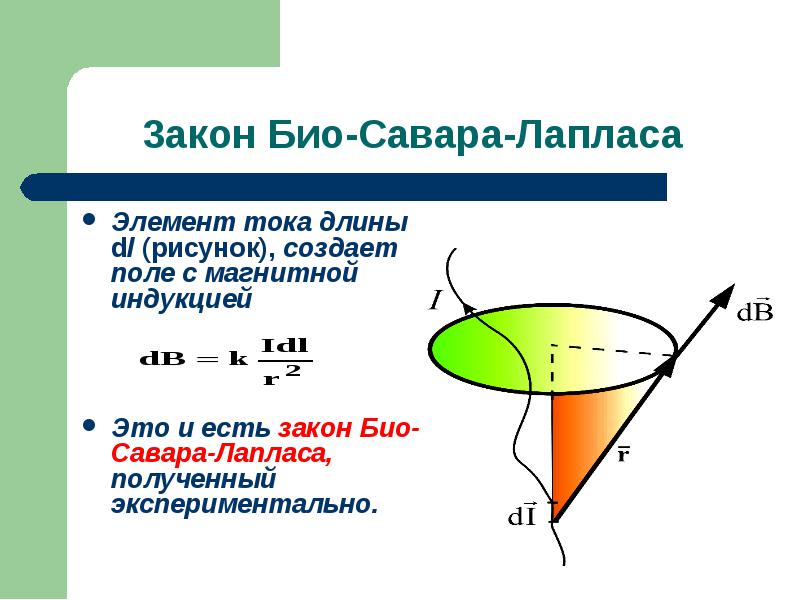Закон Био-Савара-Лапласа

Существуют формулы, описывающие этот закон для отдельных случаев МП:

поля прямого перемещения электронов;
поля кругового движения заряженных частиц.

Формула для МП первого типа имеет вид:

В = µ* µ0*2*I/4*π*r.

Для кругового движения она выглядит так:

В = µ*µ0*I/4*π*r.

В этих формулах µ – это магнитная проницаемость среды (относительная).

Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.

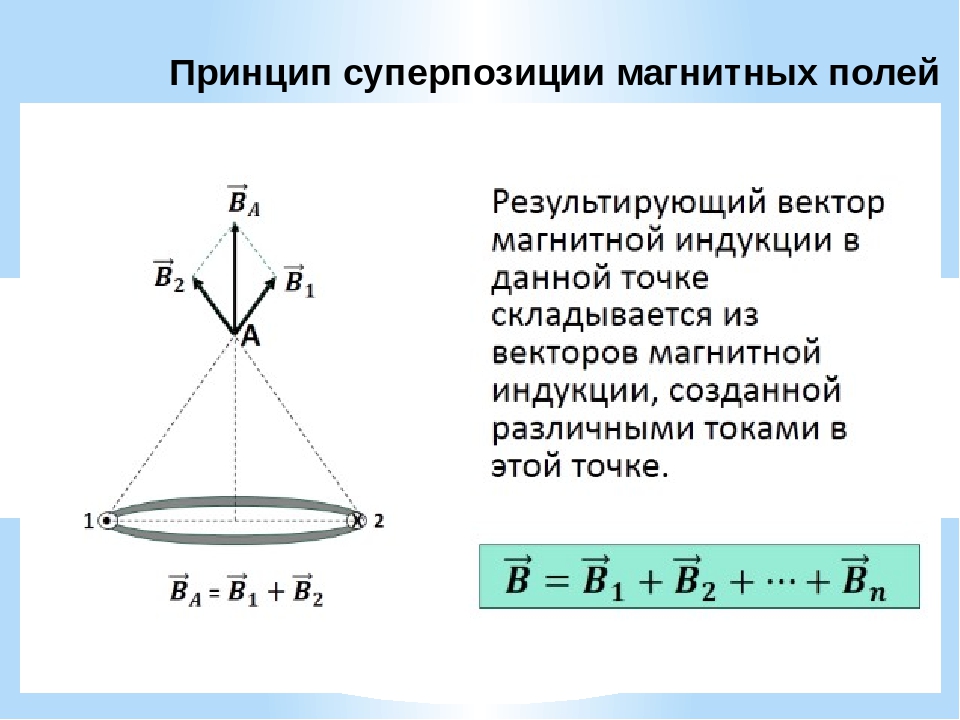
Принцип суперпозиции

Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:

B→= B1→+ B2→+ B3→… + Bn→

Принцип суперпозиции

Теорема о циркуляции

Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.

Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.

Другое название теоремы – закон Ампера, описывающий циркуляцию МП.

Математически теорема записывается следующим образом.

Математическая формула теоремы о циркуляции

где:

B→– вектор магнитной индукции;
j→ – плотность движения электронов.

Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.

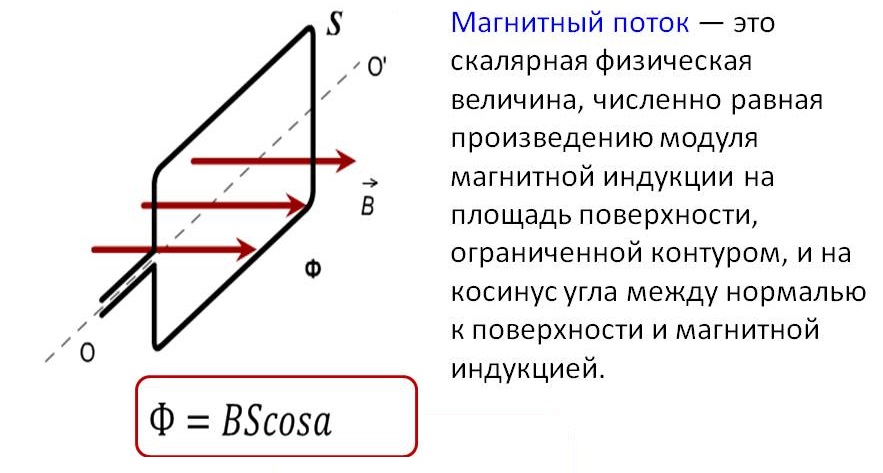
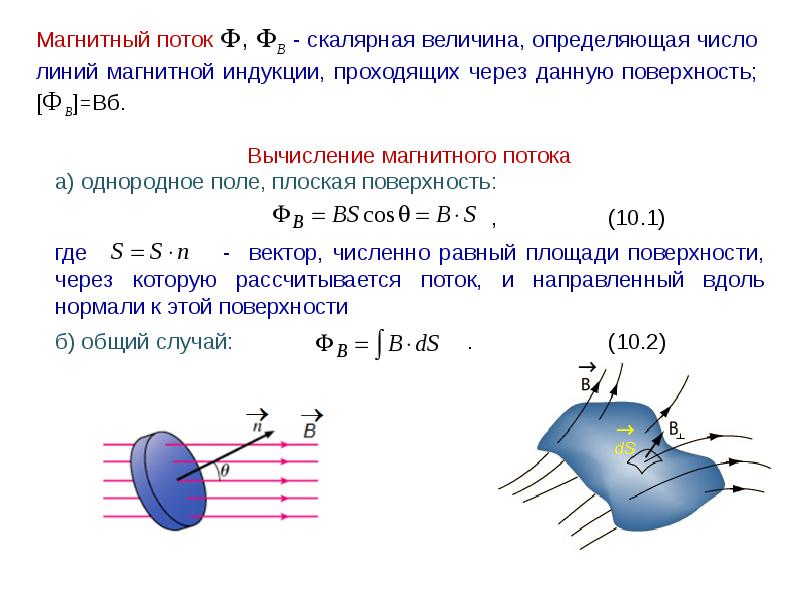
Магнитный поток

Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):

108 Мкс = 1 Вб.

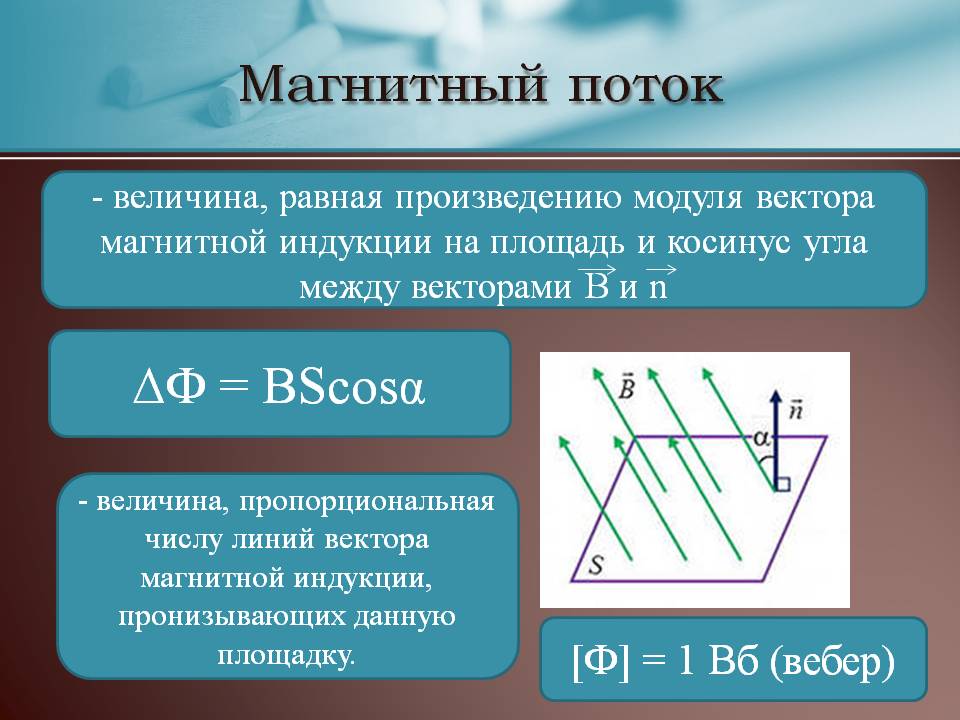
Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.

Формула для расчёта имеет вид:

φ = |B*S| = B*S*cosα,

где

В – скалярная величина градиента магнитной индукции;
S – площадь пересекаемой поверхности;
α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).

Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900)

Магнитный поток

Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.

ÐÐ¸Ð´Ñ ÐºÐ°ÑÑÑÐµÐº

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

(Здесь формулы приведем в СИ, в виде для вакуума, где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе наиболее важными являются:

Закон Био — Савара — Лапласа: играет в магнитостатике ту же роль, что закон Кулона в электростатике:

B→(r→)=μ4π∫L1I(r→1)dL1→×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int \limits _{L_{1}}{\frac {I\left({\vec {r}}_{1}\right){\vec {dL_{1}}}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}

B→(r→)=μ4π∫j→(r→1)dV1×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int {\frac {{\vec {j}}\left({\vec {r}}_{1}\right)dV_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}
Теорема Ампера о циркуляции магнитного поля:

∮∂S⁡B→⋅dl→=μIS≡μ∫Sj→⋅dS→,{\displaystyle \oint \limits _{\partial S}{\vec {B}}\cdot {\vec {dl}}=\mu _{0}I_{S}\equiv \mu _{0}\int \limits _{S}{\vec {j}}\cdot {\vec {dS}},}

rotB→≡∇→×B→=μj→.{\displaystyle \mathrm {rot} \,{\vec {B}}\equiv {\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {j}}.}

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции B→{\displaystyle {\vec {B}}}:

Три из четырех уравнений Максвелла (основных уравнений электродинамики)

divE→=ρε, rotE→=−∂B→∂t{\displaystyle \mathrm {div} \,{\vec {E}}={\frac {\rho }{\varepsilon _{0}}},\ \ \ \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}}

divB→=, rotB→=μj→+1c2∂E→∂t{\displaystyle \mathrm {div} \,{\vec {B}}=0,\ \ \ \ \,\mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}}

а именно:

Закон отсутствия монополя:

divB→=,{\displaystyle \mathrm {div} \,{\vec {B}}=0,}

Закон электромагнитной индукции Фарадея:

rotE→=−∂B→∂t,{\displaystyle \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}

Закон Ампера — Максвелла:

rotB→=μj→+1c2∂E→∂t.{\displaystyle \mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}.}

Формула силы Лоренца:

F→=qE→+qv→×B→,{\displaystyle {\vec {F}}=q{\vec {E}}+q\left,}

Следствия из неё, такие как

Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)

dF→=Idl→×B→,{\displaystyle d{\vec {F}}=\left,}

dF→=j→dV×B→,{\displaystyle d{\vec {F}}=\left,}

выражение для момента силы, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):

M→=m→×B→,{\displaystyle {\vec {M}}={\vec {m}}\times {\vec {B}},}

выражение для потенциальной энергии магнитного диполя в магнитном поле:

U=−m→⋅B→,{\displaystyle U=-{\vec {m}}\cdot {\vec {B}},}

а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:

F→=Kqmr→r3.{\displaystyle {\vec {F}}=K{\frac {q_{m}{\vec {r}}}{r^{3}}}.}

(это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

Выражение для плотности энергии магнитного поля

w=B22μ{\displaystyle w={\frac {B^{2}}{2\mu _{0}}}}

Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Вариометр

Что такое катушка, показано выше на простых примерах. На практике для обозначения однотипных групп применяют специфическую терминологию. Вариометром, например, называют деталь с переменной индуктивностью. В типовой конструкции применяют две катушки, установленные одна внутри другой. Необходимый результат получают регулировкой взаимного положения функциональных компонентов. Для перемещения применяют ручной привод или автоматизированный механизм с внешней схемой управления.

К сведению. Не следует путать определения. Мультипликаторная катушка, например, – это приспособление для рыбной ловли. Такое устройство будет обладать индуктивностью при наматывании лески из проводящего материала. Однако в радиотехнических схемах подобные устройства не используют.

Мультипликаторные катушки

Особенности других конструкций:

Дроссель обеспечивает высокое сопротивление цепи переменному току, поэтому такой пассивный индуктивный элемент часто применяют для создания фильтров. При подключении к сети питания 220В/ 50 Гц используют железные сердечники. При повышении частоты – ферритовые аналоги.
Контурные катушки магнитные устанавливают в комбинации с конденсаторами для создания схем с определенной полосой пропускания.
Электрическим реактором называют крупные конструкции, которые применяют в силовых сетях.
Сдвоенные катушки применяют для разделения цепей по постоянной составляющей.

Токовый реактор ограничивает сильный ток, предотвращает развитие аварийной ситуации при КЗ

Выше отмечены типовые области применения элементов с индуктивными характеристиками. Они пригодны для создания фильтров, ограничения тока и разделения цепи прохождения постоянных и переменных составляющих сигнала. Магнитное поле катушки с током распространяется в пространстве. Чтобы предотвратить паразитное воздействие, отдельные компоненты размещают на достаточном расстоянии.

ÐÑÑÐ¾ÑÐ¸Ñ

Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

Величина параметра никогда не может быть меньше нуля.
Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

Свойства магнетизма

Магнитное поле, как и любое другое физическое явление на Земле, имеет свои характеристики:

Источник возникновения – движущиеся электрические заряды.
Индукция магнитного поля – основная силовая его характеристика, которая существует в каждой отдельной его точке и является направленной.
Его влияние ограничивается магнитами, движущимися зарядами и проводниками тока.
Оно разделяется учеными на два типа: постоянное и переменное.
Человек без специальных приборов не может почувствовать воздействие магнетизма.
Это электродинамическое явление, ведь источник его происхождения – движущиеся частицы электрического тока. И только такие же частицы могут быть подвержены влиянию магнитного поля.
Траектория движения заряженных частиц может быть лишь перпендикулярной.

Линии магнитной индукции

Сама индукция магнитного поля характеризуется определенным направлением, представляющим собой линии, отображаемые графически. Эти линии, также получили название магнитных линий, или линий магнитных полей. Так же, как и магнитная индукция, ее линии имеют собственное определение. Они представляют собой линии, к которым проведены касательные во всех точках поля. Эти касательные и вектор магнитной индукции совпадают между собой.

Однородное магнитное поле отличается параллельными линиями магнитной индукции, совпадающими с направлением вектора во всех точках.

Если же магнитное поле является неоднородным, произойдет изменение вектора электромагнитной индукции в каждой пространственной точке, расположенной вокруг проводника. Касательные, проведенные к этому вектору, приведут к созданию концентрических окружностей вокруг проводника. Таким образом, в данном случае, линии индукции будут выглядеть в виде расширяющихся окружностей.

Материал сердечника

Как и в предыдущем примере, для вычисления индукции катушки с сердечником в представленные выше формулы добавляют множитель относительной магнитной проницаемости «m

L = m0 * m * N2 * (S/l) = m0 * m * n2 * V.

С помощью этого коэффициента учитывают ферромагнитные свойства определенного материала.

Если для примера взять бесконечный (очень длинный) прямой провод с круглым сечением, то он будет обладать определенной индуктивностью:

L = (m0/2π) * l *(mc * ln(l/r) +1/4m,

где:

mc – магнитная проницаемость (относительная) среды;
r – радиус, который намного меньше длины (l) проводника.

Однако простые зависимости действуют только до определенной частоты. С определенного уровня волны малой длины начинают распространяться в поверхностной части проводников (скин-эффект). Дополнительно приходится учитывать влияние вихревых составляющих, экранирующих излучение и меняющих силовые параметры поля.

Современные магнитные материалы

Катушка будет работать в точном соответствии с расчетом, если правильно подобраны все функциональные компоненты конструкции. Как показано выше, существенное значение имеют параметры сердечника. Ниже отмечены важные особенности соответствующих материалов:

Сталь с низким содержанием примесей стоит недорого. Ее рекомендуется применять в цепях постоянного тока, так как при повышении частоты значительно увеличиваются потери.
В специальные сорта (трансформаторную сталь) добавляют кремний. Для уменьшения вредного влияния поверхностных эффектов сердечник собирают из пластин. Однако и такие решения не следует использовать при частоте более 1 кГц.
Сплавы из железа с никелем отличаются увеличенной магнитной проницаемостью. Рабочий диапазон – до 80-120 кГц.
Порошковые материалы создают со слоем диэлектрика на поверхностях отдельных микроскопических гранул. Они хорошо приспособлены для работы с высокочастотными сигналами, однако не обладают большой магнитной проницаемостью.
Ферриты – это материалы, созданные на основе керамических компонентов. Они отличаются хорошими техническими характеристиками, малыми потерями. Следует учитывать значительную зависимость от температуры, а также ухудшение рабочих параметров при длительной эксплуатации.

Измерение индуктивности катушки, созданной из медного провода на ферритовом сердечнике

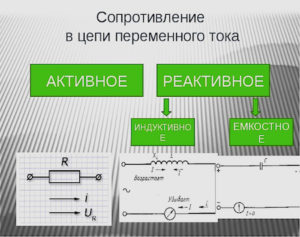
Как найти активную, реактивную и полную мощность

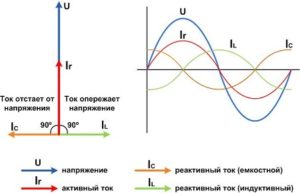
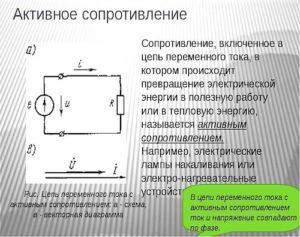
Активная мощность относится к энергии, которая необратимо расходуется источником за единицу времени для выполнения потребителем какой-либо полезной работы. В процессе потребления, как уже было отмечено, она преобразуется в другие виды энергии.

В цепи переменного тока значение активной мощности определяется, как средний показатель мгновенной мощности за установленный период времени. Следовательно, среднее значение за этот период будет зависеть от угла сдвига фаз между током и напряжением и не будет равной нулю, при условии присутствия на данном участке цепи активного сопротивления. Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.

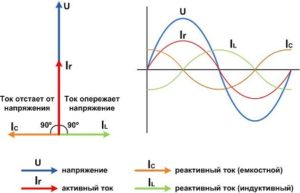
При выполнении расчетов электрических цепей широко используется понятие реактивной мощности. С ее участием происходят такие процессы, как обмен энергией между источниками и реактивными элементами цепи. Данный параметр численно будет равен амплитуде, которой обладает переменная составляющая мгновенной мощности цепи.

Существует определенная зависимость реактивной мощности от знака угла ф, отображенного на рисунке. В связи с этим, она будет иметь положительное или отрицательное значение. В отличие от активной мощности, измеряемой в ваттах, реактивная мощность измеряется в вар – вольт-амперах реактивных. Итоговое значение реактивной мощности в разветвленных электрических цепях представляет собой алгебраическую сумму таких же мощностей у каждого элемента цепи с учетом их индивидуальных характеристик.

Основной составляющей полной мощности является максимально возможная активная мощность при заранее известных токе и напряжении. При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).