- Направление вектора МИ
- Наглядное отображение линий МИ
- Основные формулы раздела «Электромагнитная индукция»
- Измерительные приборы
- Законы электролиза
- Примечания
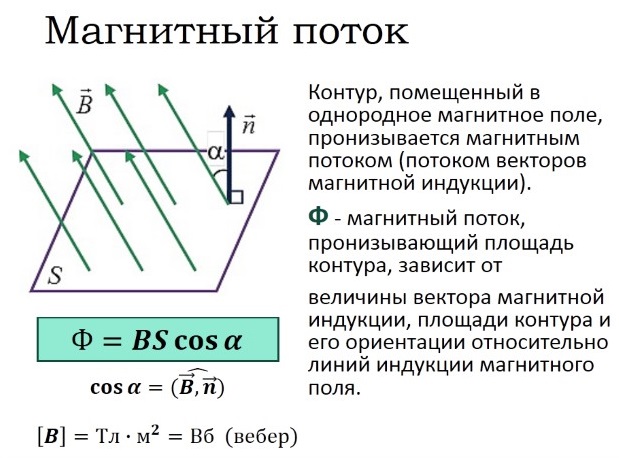
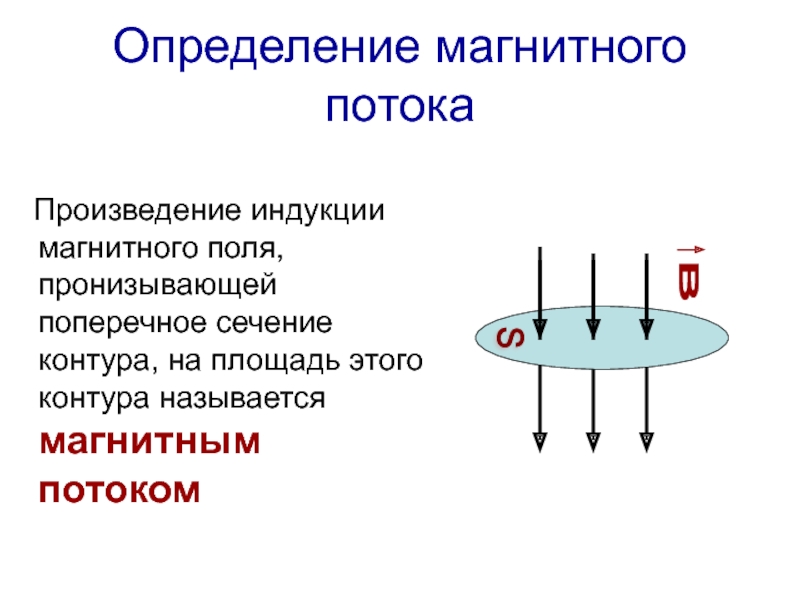
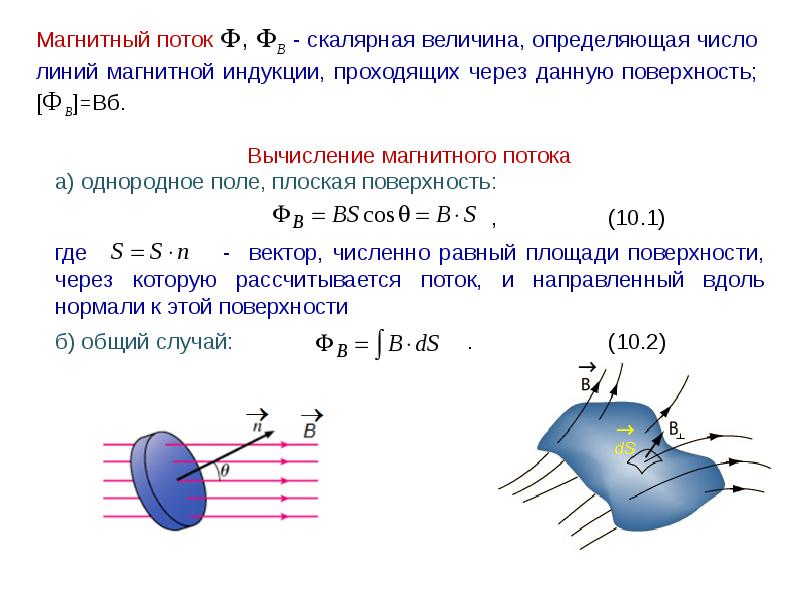
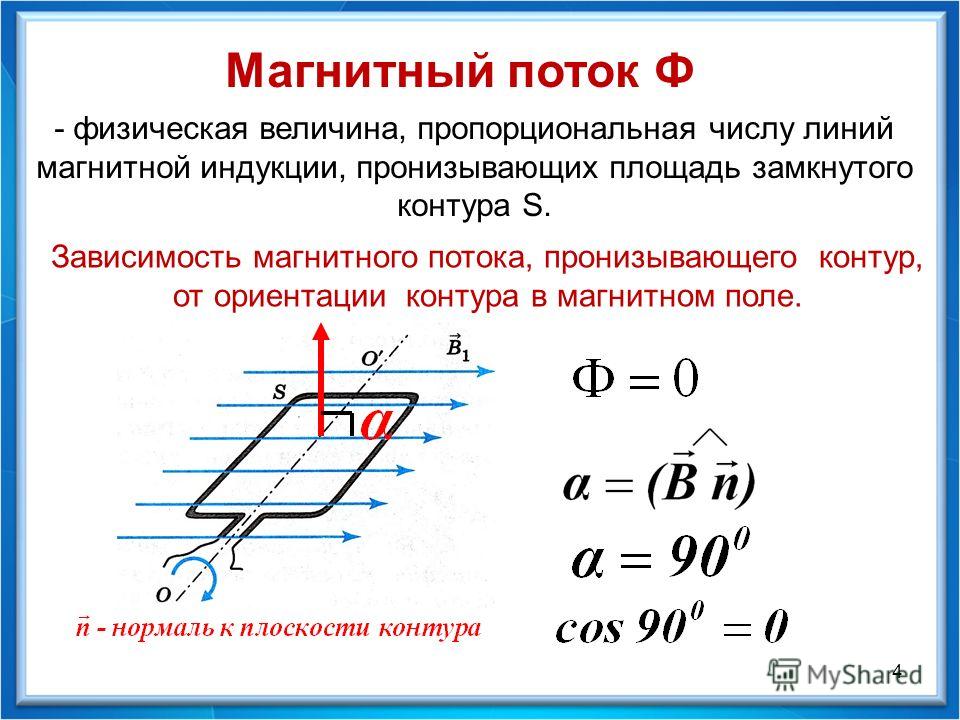
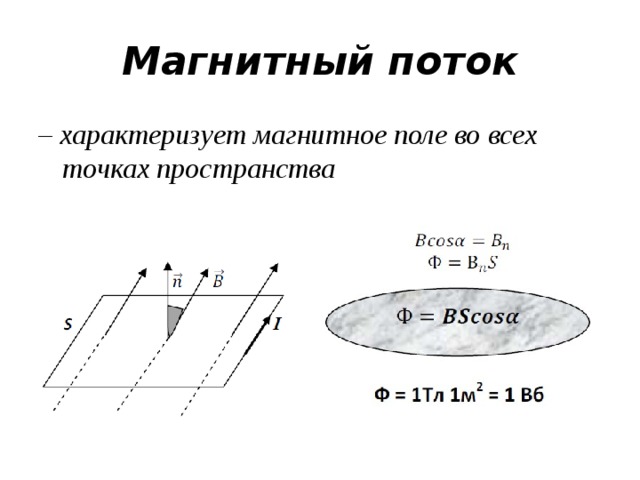
- Магнитный поток
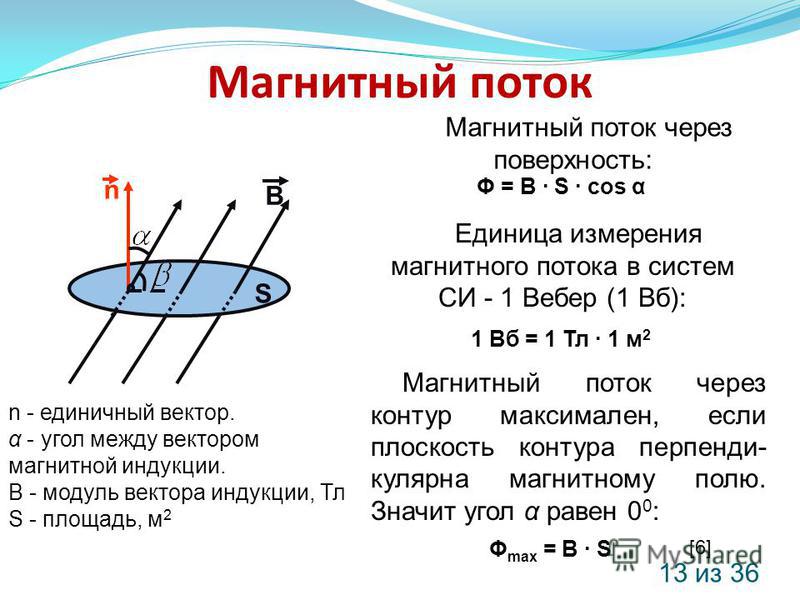
- Магнитный поток
- Магнитное поле[править]
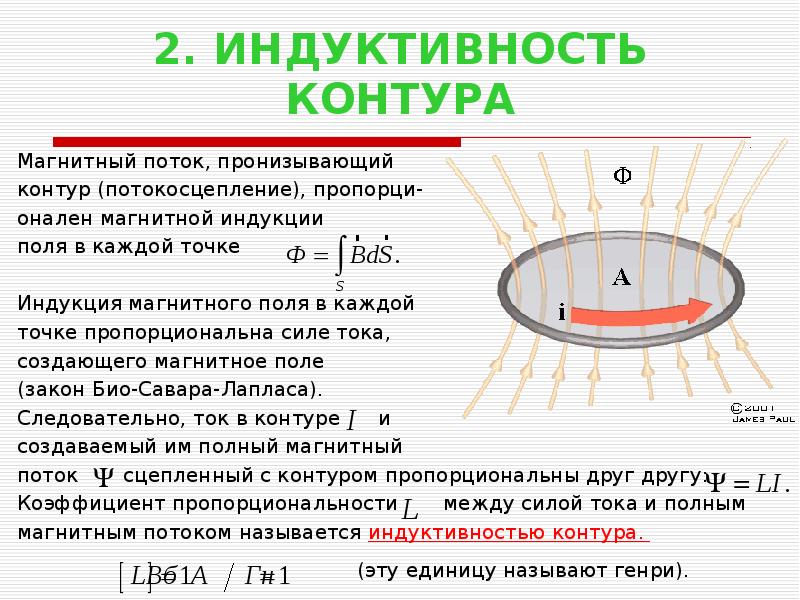
- Индуктивность
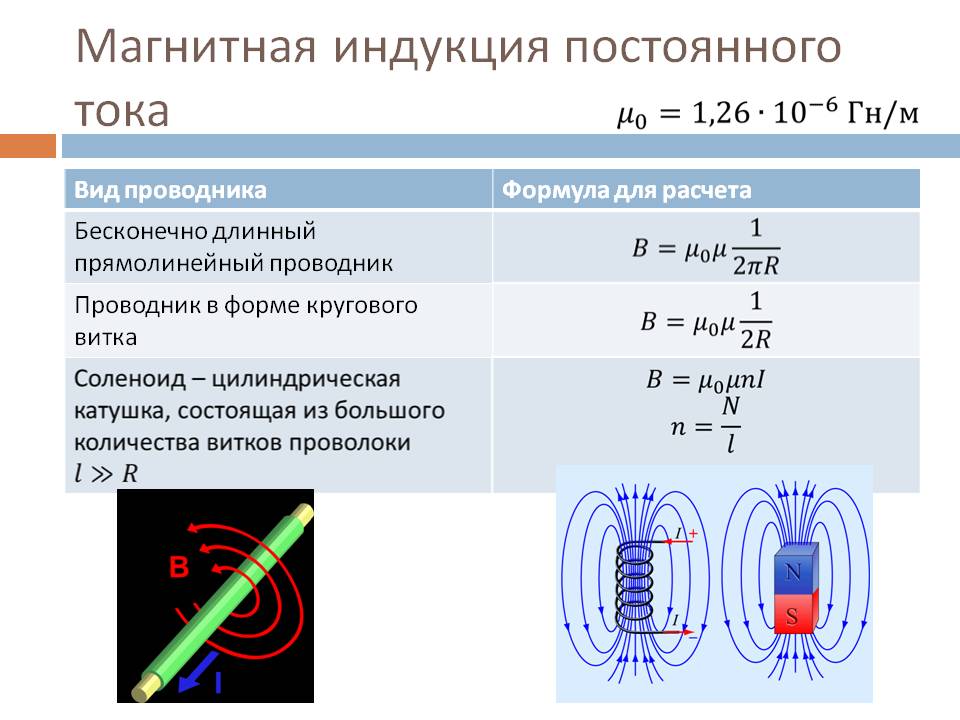
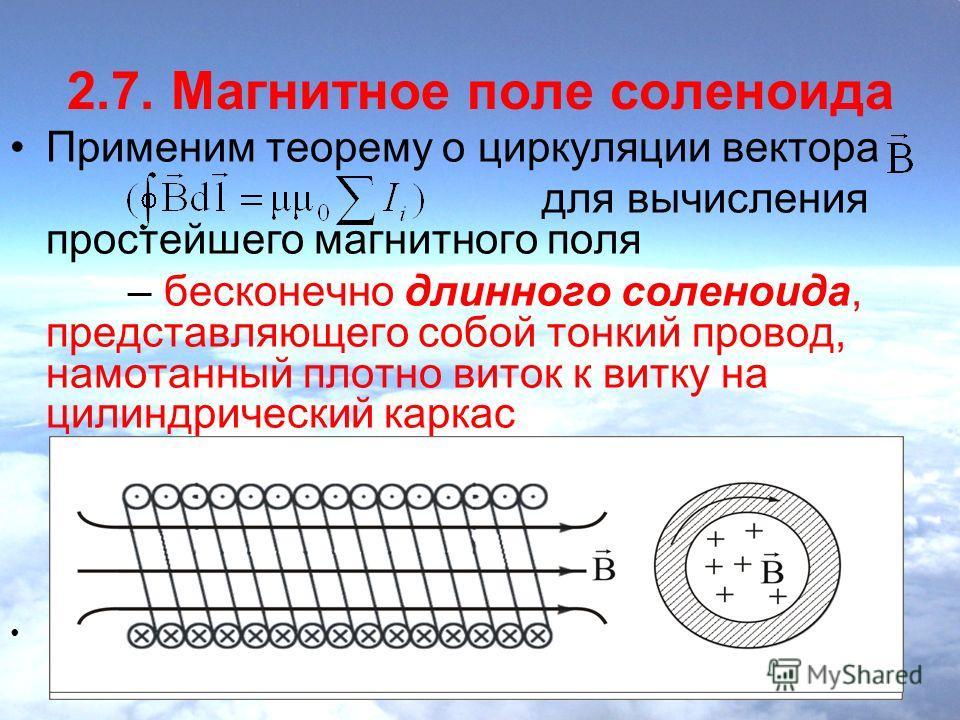
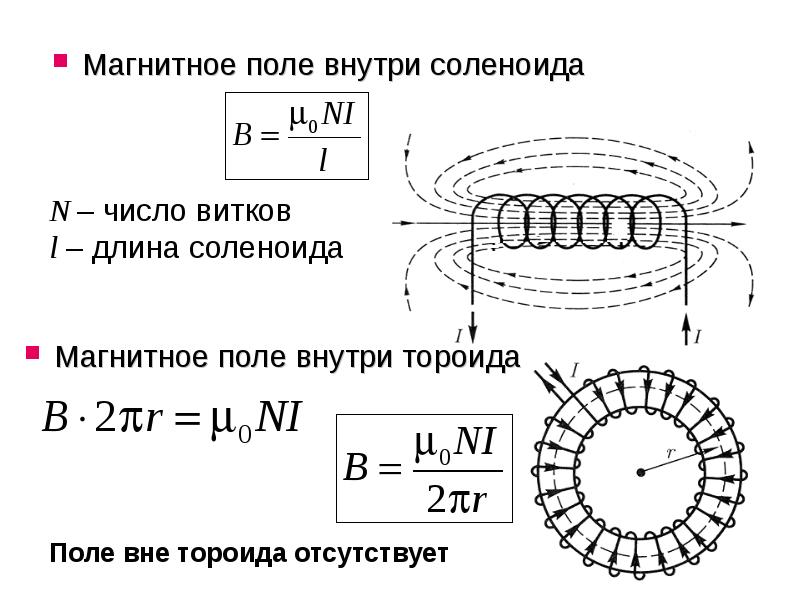
- Магнитное поле
- Основные уравнения
- В магнитостатике
- В общем случае
- Закон электромагнитной индукции Фарадея
- Векторная форма
- Потенциальная форма
- Изменения в магнитосфере Земли
- Паразитная индукция и тепловые потери
- Расслоение электромагнита
- Паразитные потери в катушках индуктивности
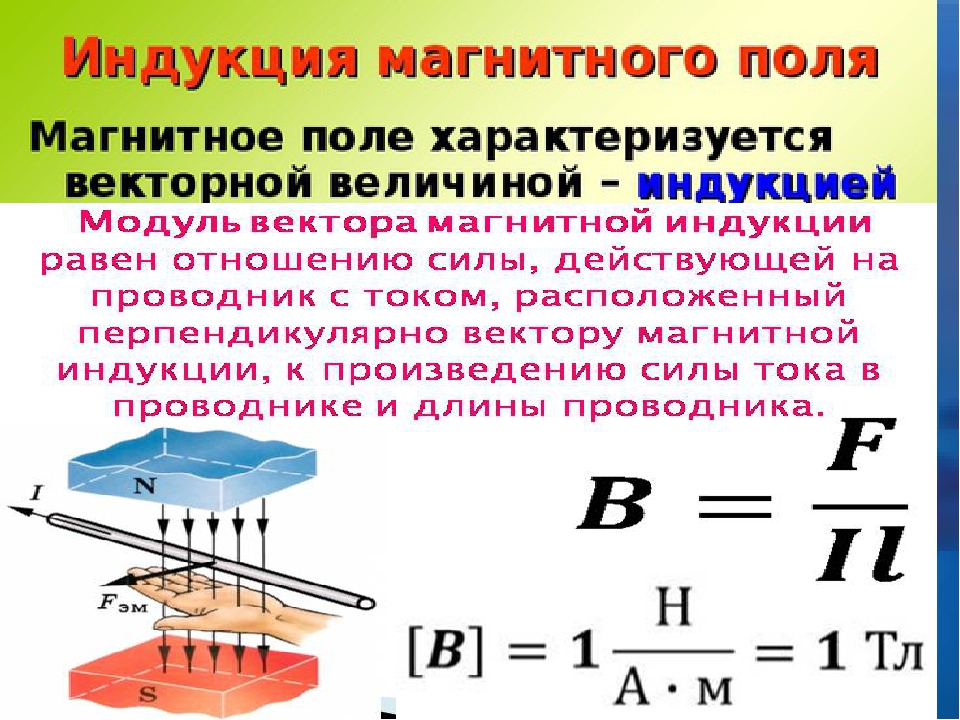
- Физический смысл магнитной индукции
- Взаимодействие магнита с контуром
- Направление вектора МИ
- Наглядное отображение линий МИ
- Заказать решение ТОЭ
- Вращающаяся катушка
- Явление электромагнитной индукции
- Магнитосфера Земли
Направление вектора МИ
Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.
Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.
Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали
В некоторых случаях, чтобы найти направление, применяют правило правой руки.
 Определение направления B→
Определение направления B→
Наглядное отображение линий МИ
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.
С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.
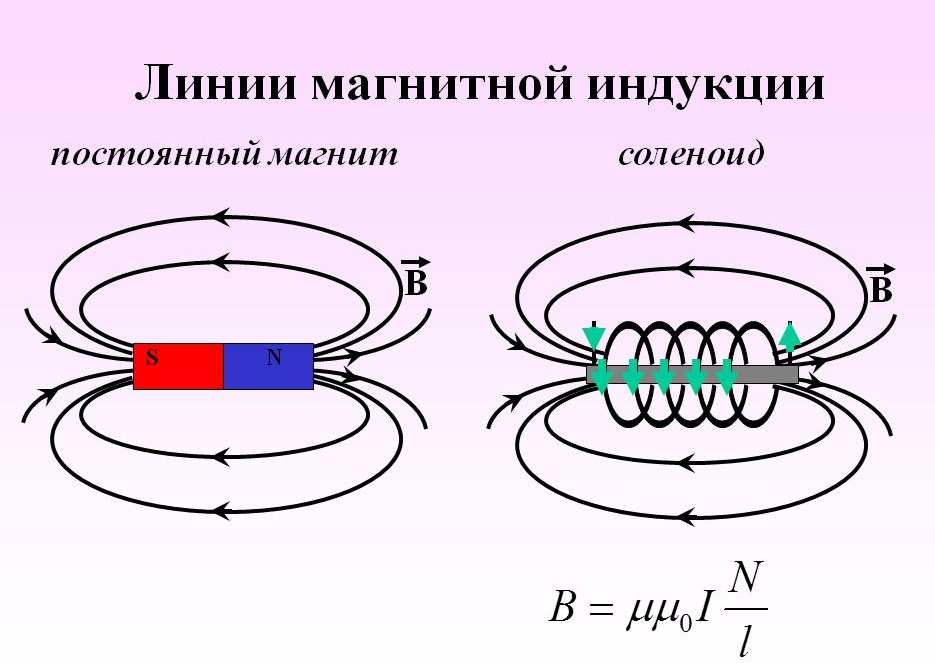 Графическое обозначение линий МИ
Графическое обозначение линий МИ
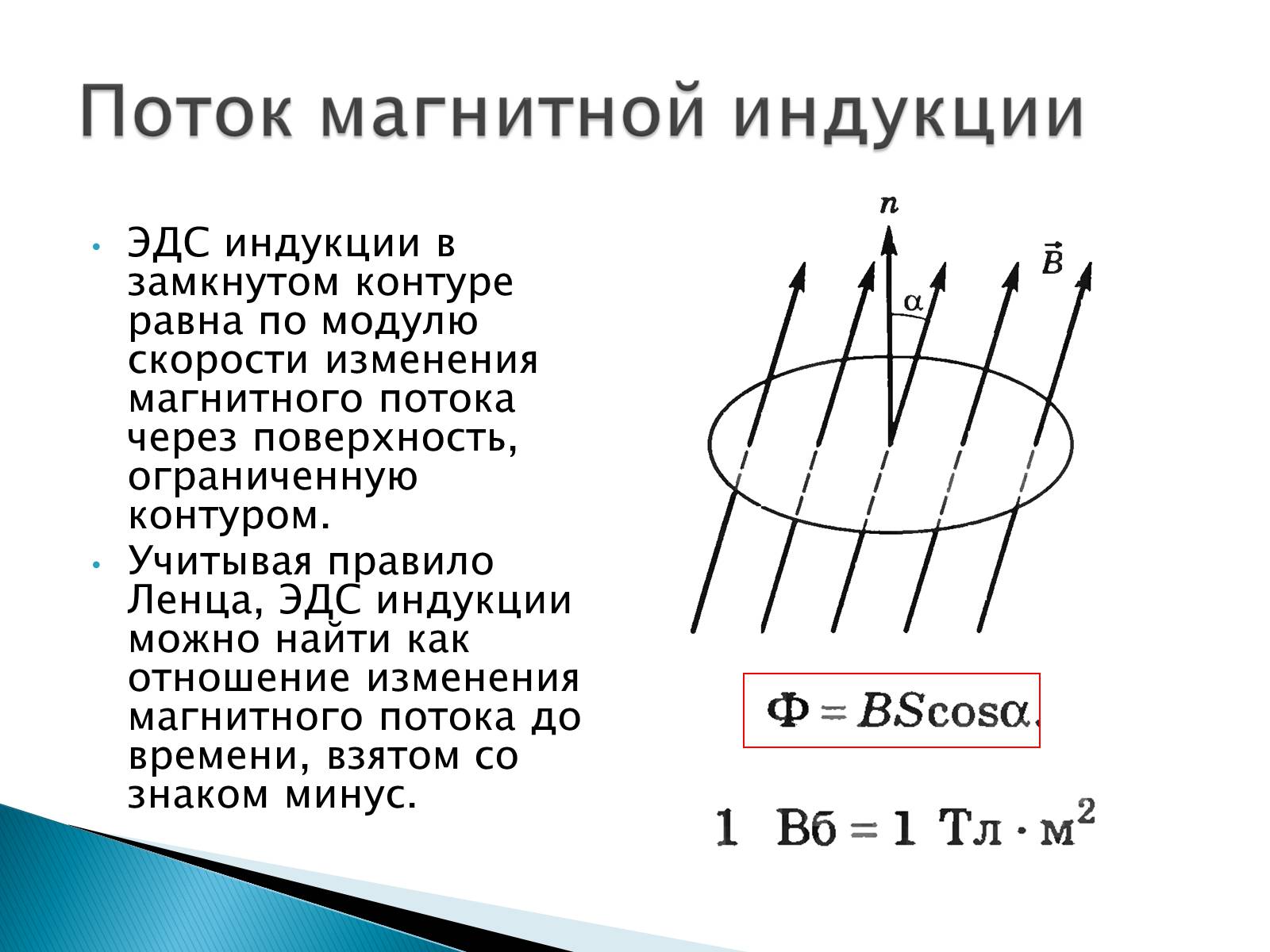
Основные формулы раздела «Электромагнитная индукция»
Для упрощения расчетов ниже приведены алгоритмы тематических вычислений:
- закон магнитной индукции – E = – (ΔФ/Δt);
- магнитный поток – Ф = В * S * cos α;
- закон ЭДС для движущегося проводника – Ev = В * D * v * sin α;
- электродвижущая сила самоиндукции катушки – Ec = -L*(ΔI/Δt);
- магнитный поток (индуктивность) – Ф = L*I (L= Ф/I);
- энергия, которую в соответствии с законом индукции накапливает катушка, – W = (L * I2)/2.
Как использовать приведенные формулы на практике, рассказано выше. В расчетах следует учитывать определенное значение электрических параметров, скорость перемещения и геометрию проводника.
Измерительные приборы
Магнитные потоки, определимые с помощью специальных приборов – флюксметров, измеряются и в лабораторных, и в полевых условиях. Приборы ещё называют веберметрами. Особенностью такого измерительного аппарата магнитоэлектрической системы (МЭС) является то, что ток подводится к перемещающейся бескаркасной рамке через спирали, не имеющие момента противодействия (безмоментные).
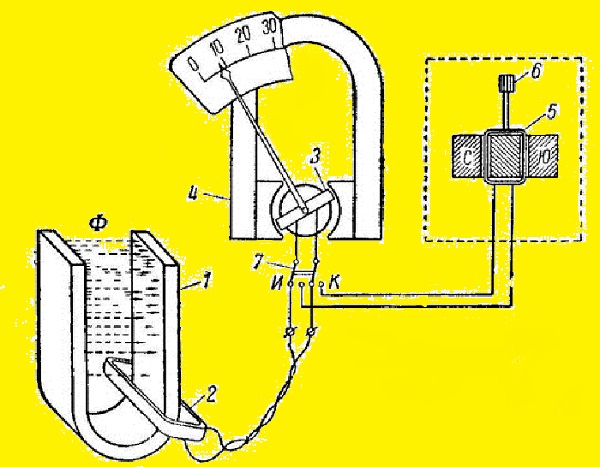 Схема применения и устройства флюксметра
Схема применения и устройства флюксметра
Прибор состоит из следующих деталей, отмеченных на рис. выше:
- испытуемый постоянный магнит – 1;
- рамка измерительная – 2;
- рамка прибора – 3;
- магнит прибора – 4;
- рамка корректирующего устройства – 5;
- головка регулировки корректирующей рамки – 6;
- переключатель «работа – коррекция» – 7.
Флюксметр не может измерять слабые МП из-за низкой чувствительности.
Законы электролиза
Фарадей сформулировал закон электролиза в 30-х годах 19 века. Эти правила применяют для воспроизведения соответствующих технологических процессов на производстве и в домашних условиях. В математическом виде зависимости можно представить следующим образом:
m = (q/F) * (М/V),
где:
- m – масса вещества, которое осаждается на рабочей пластине в процессе электролиза;
- q – суммарный заряд;
- F – постоянная Фарадея = 96, 485,33;
- M – молярная масса;
- V – количество элементарных зарядов на единичный ион (валентность).
Первый закон Фарадея для электролиза определяет пропорциональность осажденного вещества затраченной электроэнергии. Из базовой формулы понятно, что для этого случая существенное значение имеет пропущенный заряд (q).
Второй закон Фарадея устанавливает зависимость между количеством осажденного вещества и его свойствами. Для этой части определения подразумевается неизменный расход электроэнергии при электролизе разных материалов.
Примечания
-
Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид:
- F→=qE→+qv→×B→.{\displaystyle {\vec {F}}=q{\vec {E}}+q.}
При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведённую в основном тексте.
- Это определение с современной точки зрения менее фундаментально, чем приведённое выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
- То есть в наиболее фундаментальном и простом для ознакомления виде.
- То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближённо — если изменения настолько медленны, что ими можно пренебречь.
- Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в статье далее).
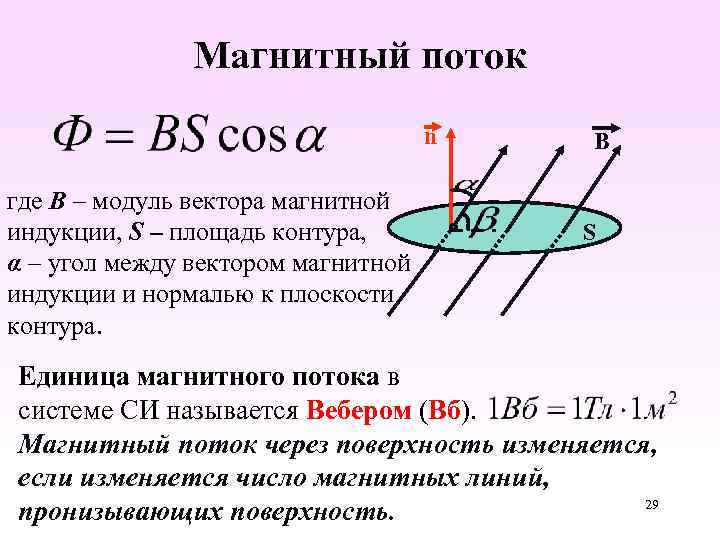
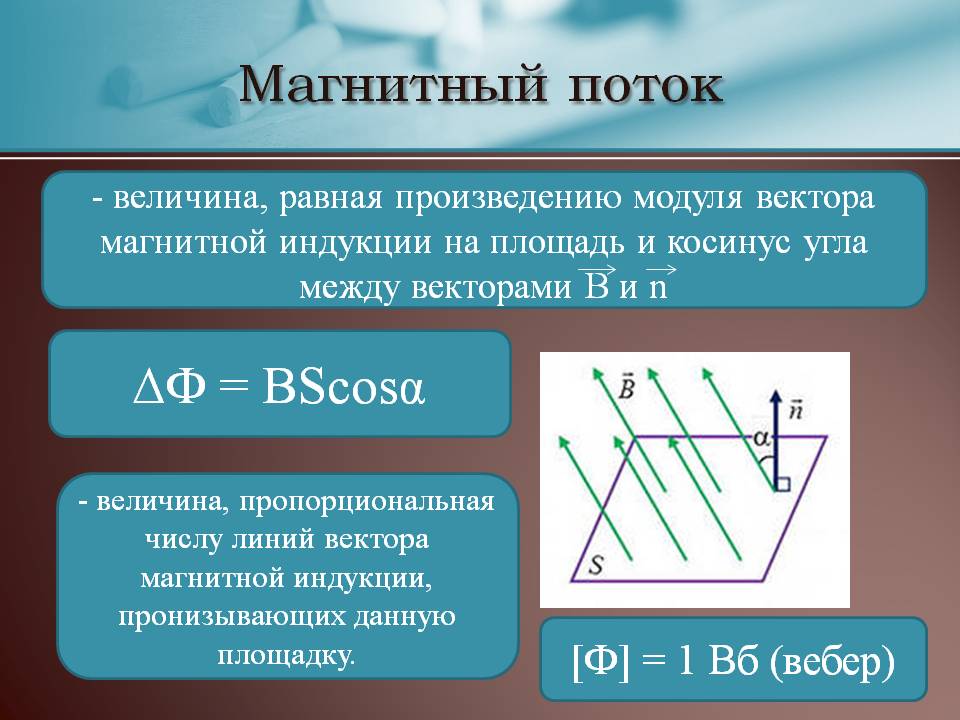
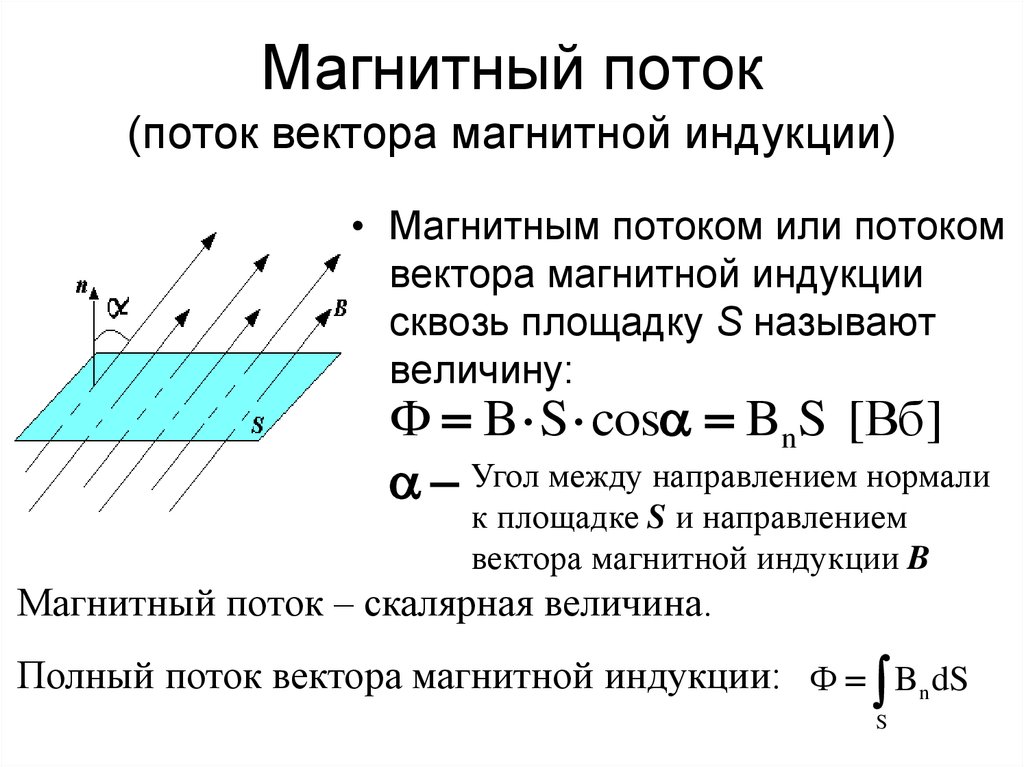
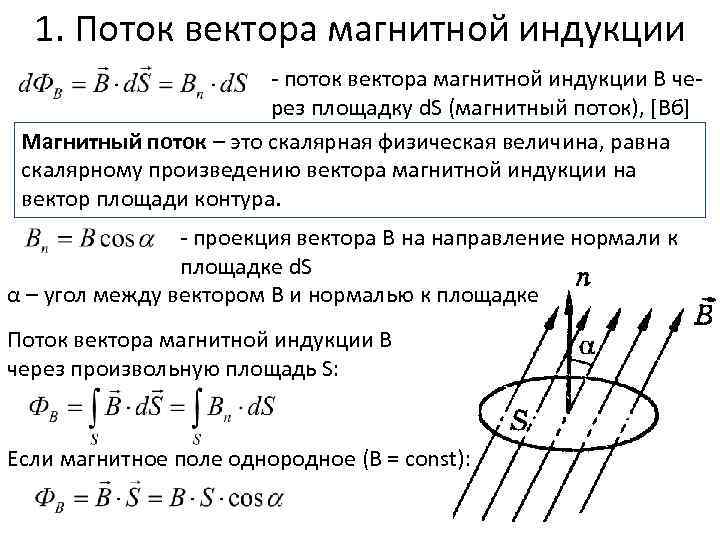
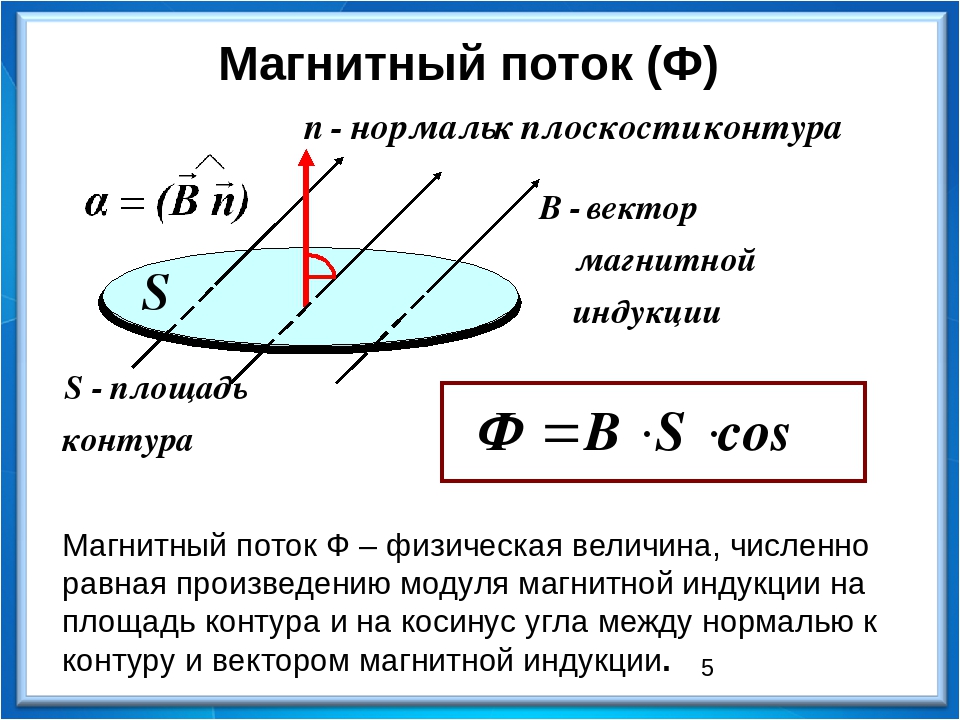
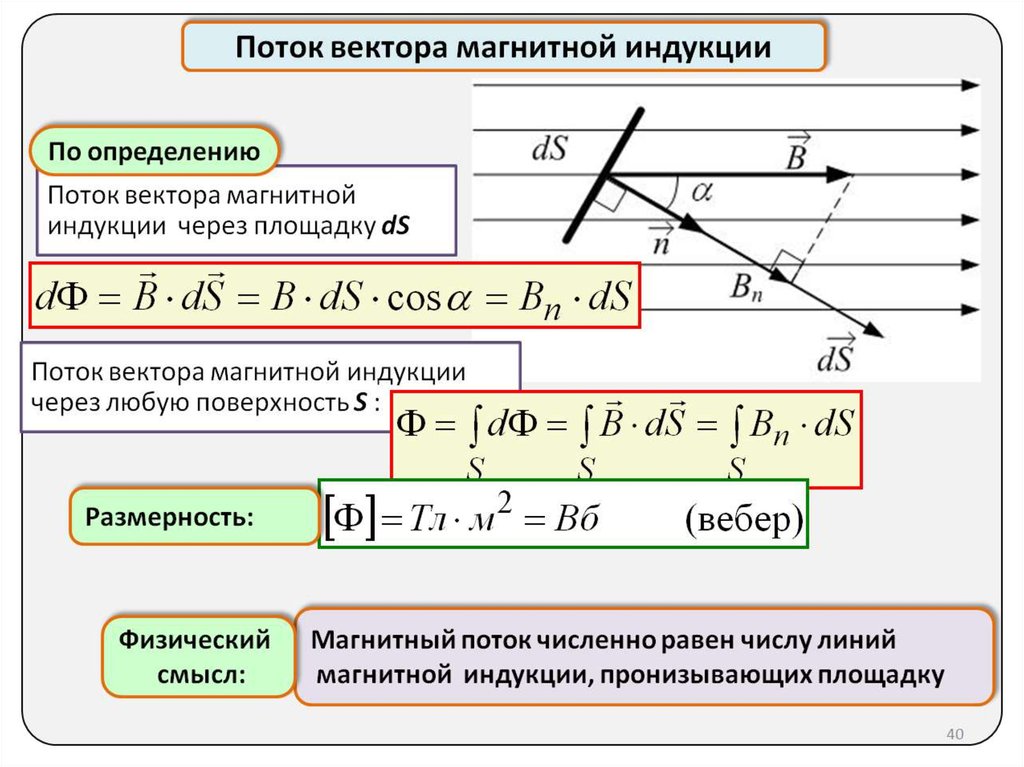
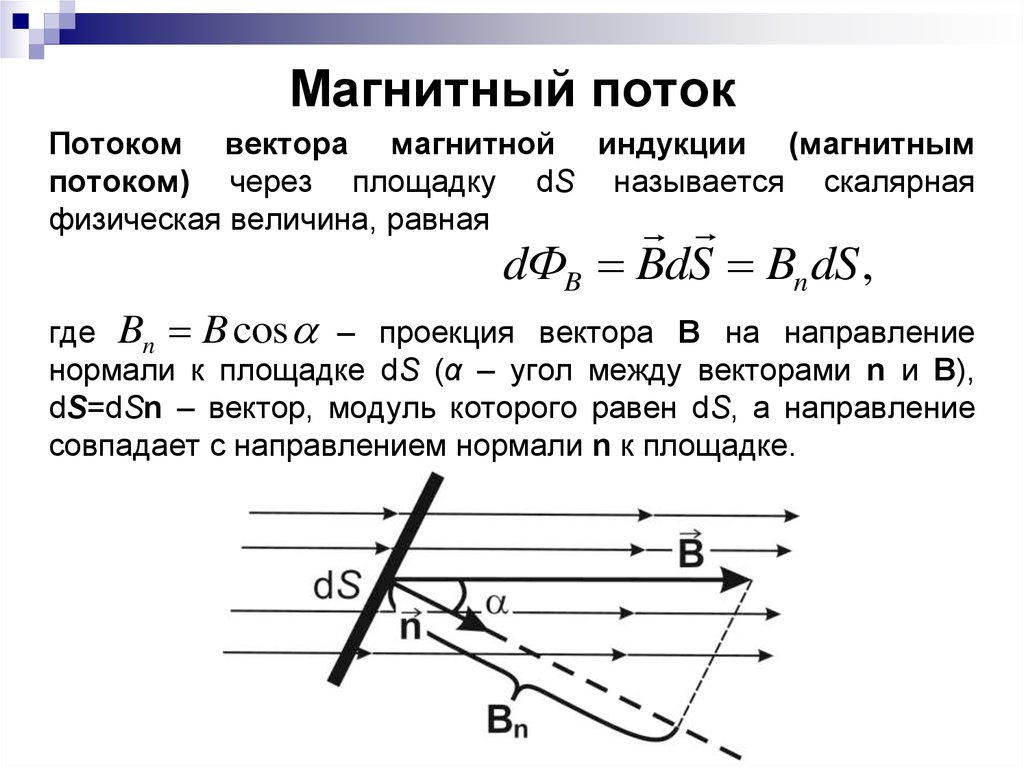
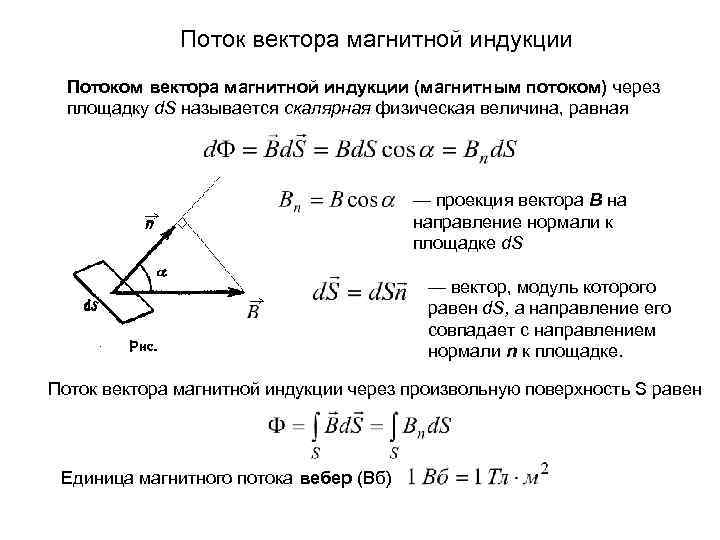
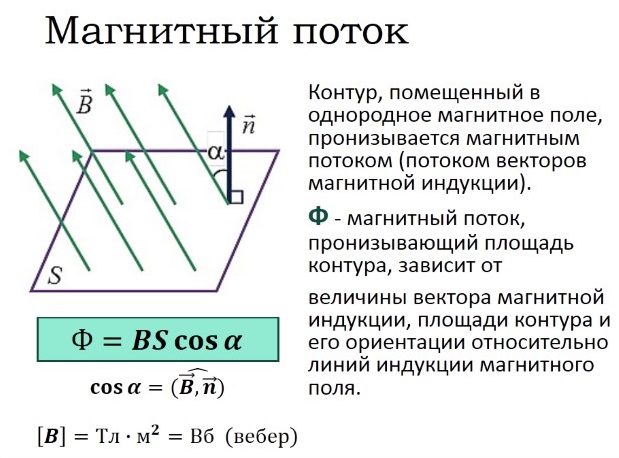
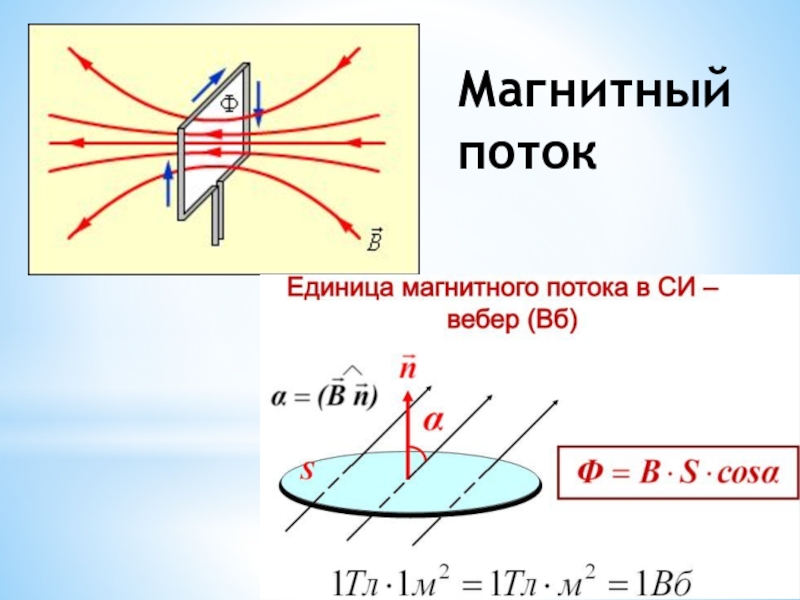
Магнитный поток
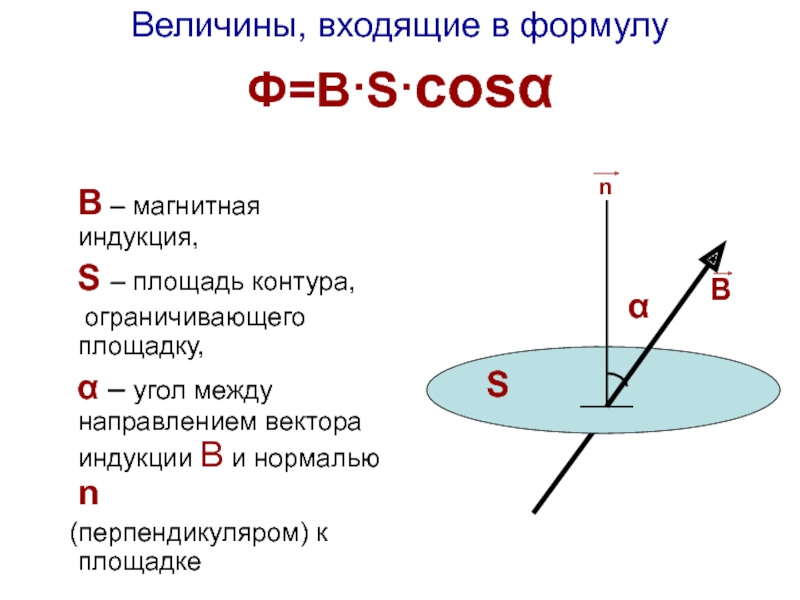
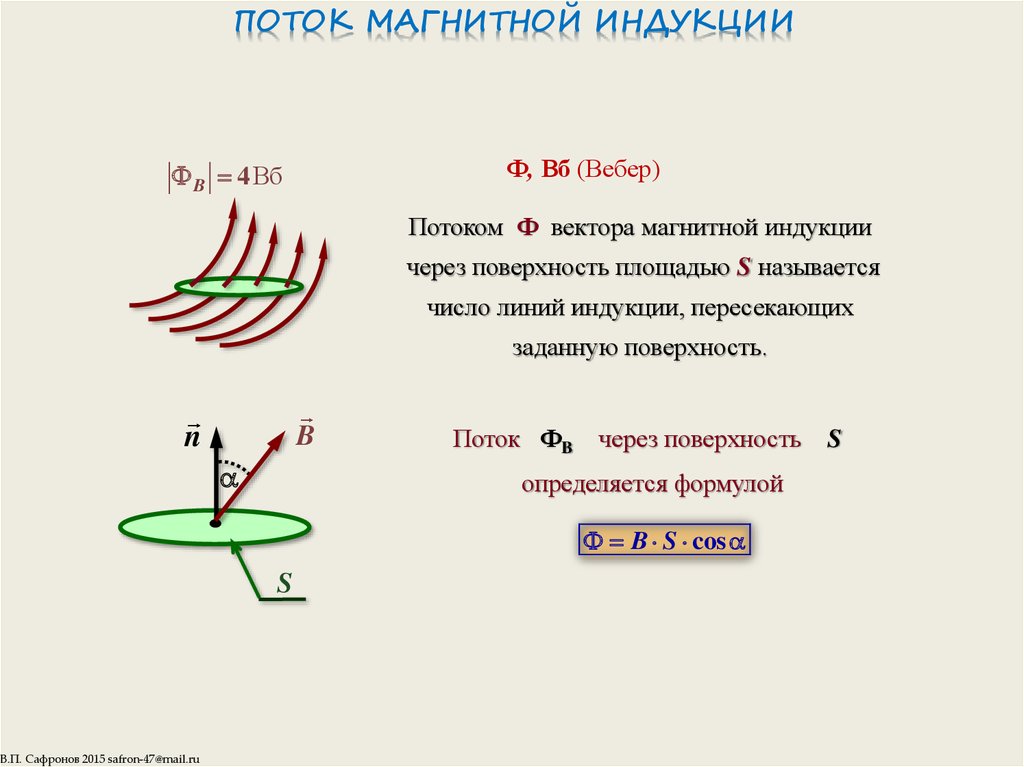
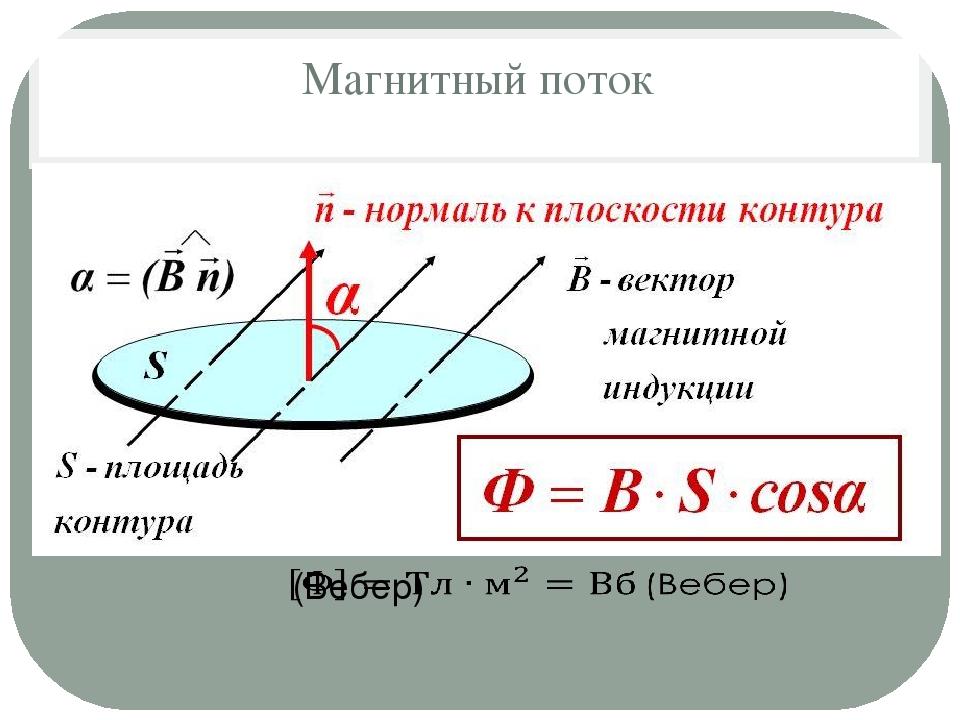
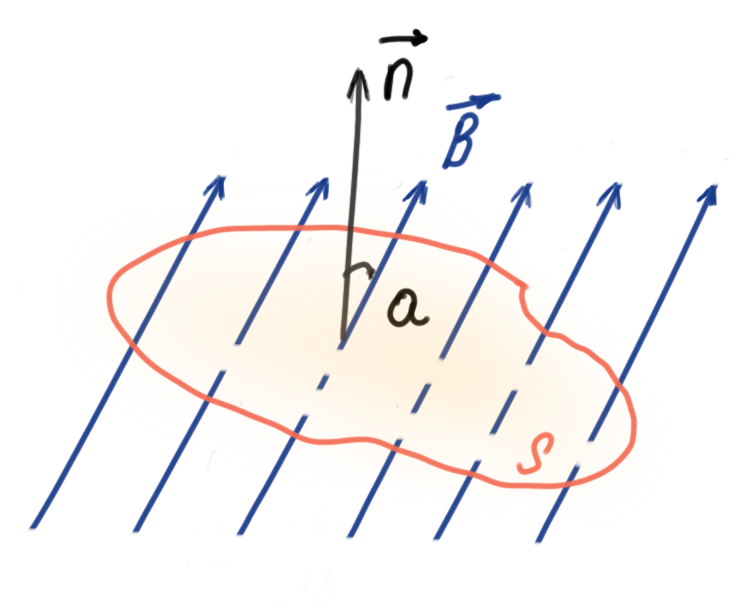
Для практических расчетов, кроме сути явления, нужны соответствующие формулы (правила). Определение магнитного потока (Ф) базируется на векторном выражении индукции (В). Значение этого параметра зависит от площади контрольной площадки (S) и угла наклона силовых линий (α). Зависимости можно выражать следующим образом:
Ф = В * S * cos α.
Если обеспечить прямой угол между поверхностью и вектором индукции, множитель cosα исключается. Для такого расположения с применением стандартов СИ будет формулироваться следующее определение: единица магнитного потока (Вебер, Вб) равна индукции поля 1 Тесла (Тл), которая пронизывает площадку 1 м кв.
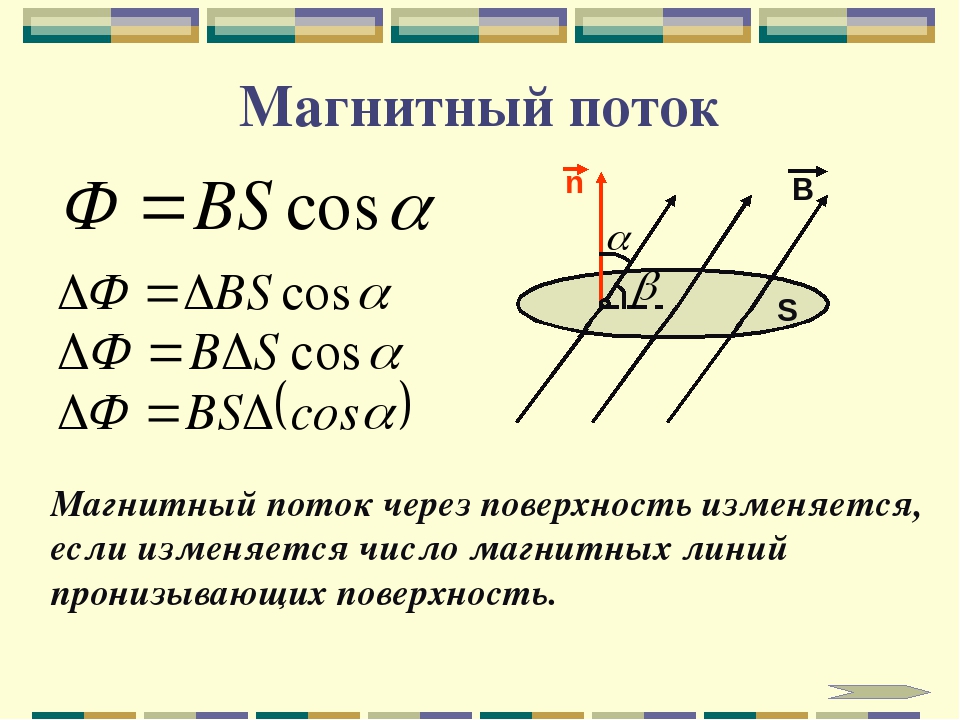
Магнитный поток
Известно, что пропускание тока через проводник сопровождается формированием электромагнитного поля. На этом принципе основана работа динамиков, запорных устройств, приводов реле, других приспособлений. Изменением параметров источника питания получают необходимые силовые усилия для перемещения (удержания) совмещенных деталей, обладающих ферромагнитными свойствами.
Однако действительно и обратное утверждение. Если между полюсами постоянного магнита перемещать рамку из проводящего материала по соответствующему замкнутому контуру, начнется перемещение заряженных частиц. Подключив соответствующие приборы, можно регистрировать изменение тока (напряжения). В ходе элементарного эксперимента можно выяснить увеличение эффекта в следующих ситуациях:
- перпендикулярное расположение проводника/силовых линий;
- ускорение перемещений.
На картинке выше показано, как определять направление тока в проводнике с помощью простого правила.
Магнитное поле[править]
В отличие от заряда покоящегося, который создает вокруг себя электрическое поле, заряд движущийся создает вокруг себя также магнитное поле .
Экспериментально установлено, что:
|
Магнитное поле создается постоянными магнитами или проводниками, по которым течет постоянный ток. Вектор магнитной индукции B является важнейшей характеристикой магнитного поля. Линии магнитной индукции — это линии, касательные к которым направлены так же, как и вектор В в данной точке. В отличие от силовых линий электростатического поля, линии магнитной индукции замкнуты. Магнитное поле является вихревым. В нем работа при перемещении по замкнутой траектории не равна нулю, а зависит от формы траектории (в отличии от электростатического поля или поля тяжести Земли).
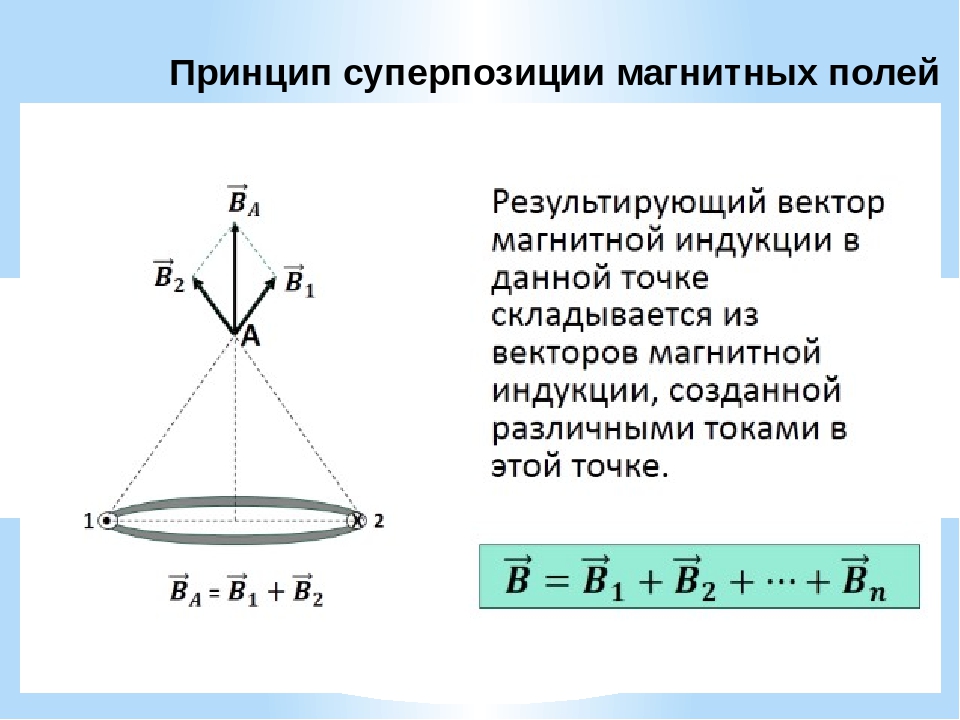
Для магнитных полей справедлив принцип суперпозиции, дадим его определение.
Определение. Принцип суперпозиции. В любой точке поля вектор магнитной индукции результирующего поля равен сумме векторов полей, создаваемых каждой точкой в отдельности: B=B1+B2+…+Bn{\displaystyle B=B_{1}+B_{2}+…+B_{n}}.
Индуктивность
Проходя по контуру, электрический ток способствует образование вокруг него совокупности магнитных силовых линий. Согласно формуле Ф = L×I, создаваемый магнитом поток Ф пропорционально зависит от силы тока I.
Таким образом, под индуктивностью L понимают коэффициент соотношения магнитного потока Ф и силы тока I, протекающего по контуру. Рассчитывают данную величину по следующей формуле:
L=Ф/I.
Единицей измерения этой физической величины является Генри (Гн). 1 Гн – это индуктивность, образующаяся в замкнутом контуре, в котором сила тока изменяется на 1 Ампер, а величина напряжения в нем составляет 1 Вольт.
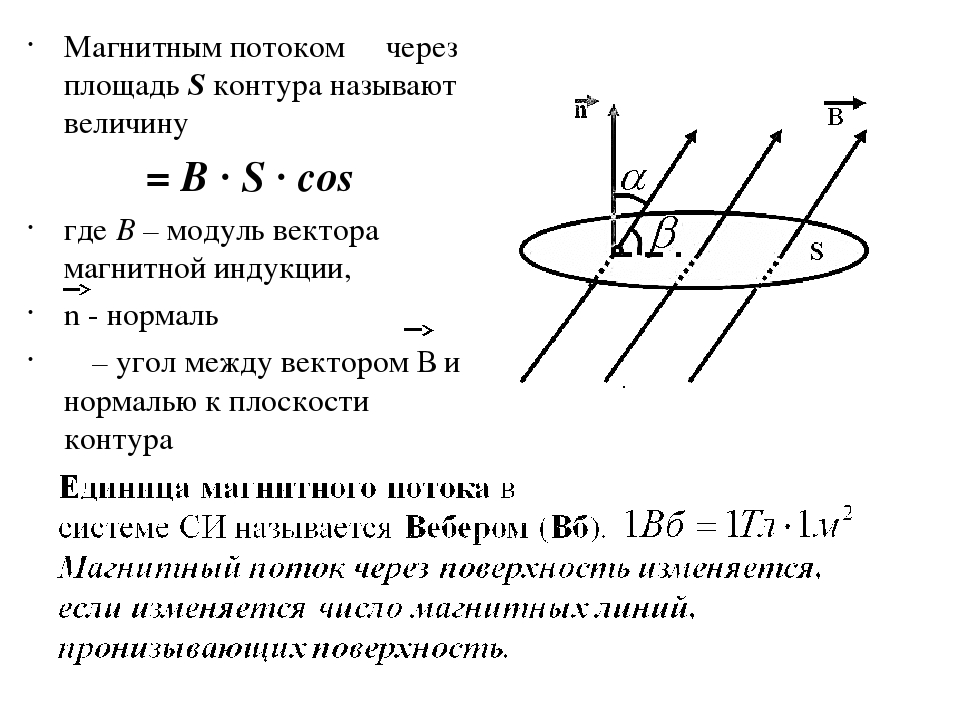
Магнитное поле
Уже в VI в. до н.э. в Китае было известно, что некоторые руды обладают способностью притягиваться друг к другу и притягивать железные предметы. Куски таких руд были найдены возле города Магнесии в Малой Азии, поэтому они получили название магнитов.
Посредством чего взаимодействуют магнит и железные предметы? Вспомним, почему притягиваются наэлектризованные тела? Потому что около электрического заряда образуется своеобразная форма материи — электрическое поле. Вокруг магнита существует подобная форма материи, но имеет другую природу происхождения (ведь руда электрически нейтральна), ее называют магнитным полем.
Для изучения магнитного поля используют прямой или подковообразный магниты. Определенные места магнита обладают наибольшим притягивающим действием, их называют полюсами (северный и южный). Разноименные магнитные полюса притягиваются, а одноименные — отталкиваются.
Для силовой характеристики магнитного поля используют вектор индукции магнитного поля B. Магнитное поле графически изображают при помощи силовых линий (линии магнитной индукции). Линии являются замкнутыми, не имеют ни начала, ни конца. Место, из которого выходят магнитные линии — северный полюс (North), входят магнитные линии в южный полюс (South).
Магнитное поле можно сделать «видимым» с помощью железных опилок.
Основные уравнения
Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.
(Здесь формулы приведем в СИ, в виде для вакуума, где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).
В магнитостатике
В магнитостатическом пределе наиболее важными являются:
-
Закон Био — Савара — Лапласа: играет в магнитостатике ту же роль, что закон Кулона в электростатике:
- B→(r→)=μ4π∫L1I(r→1)dL1→×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int \limits _{L_{1}}{\frac {I\left({\vec {r}}_{1}\right){\vec {dL_{1}}}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}
- B→(r→)=μ4π∫j→(r→1)dV1×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int {\frac {{\vec {j}}\left({\vec {r}}_{1}\right)dV_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}
-
Теорема Ампера о циркуляции магнитного поля:
- ∮∂SB→⋅dl→=μIS≡μ∫Sj→⋅dS→,{\displaystyle \oint \limits _{\partial S}{\vec {B}}\cdot {\vec {dl}}=\mu _{0}I_{S}\equiv \mu _{0}\int \limits _{S}{\vec {j}}\cdot {\vec {dS}},}
- rotB→≡∇→×B→=μj→.{\displaystyle \mathrm {rot} \,{\vec {B}}\equiv {\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {j}}.}
В общем случае
Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции B→{\displaystyle {\vec {B}}}:
Три из четырех уравнений Максвелла (основных уравнений электродинамики)
-
- divE→=ρε, rotE→=−∂B→∂t{\displaystyle \mathrm {div} \,{\vec {E}}={\frac {\rho }{\varepsilon _{0}}},\ \ \ \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}}
- divB→=, rotB→=μj→+1c2∂E→∂t{\displaystyle \mathrm {div} \,{\vec {B}}=0,\ \ \ \ \,\mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}}
- а именно:
Закон отсутствия монополя:
-
- divB→=,{\displaystyle \mathrm {div} \,{\vec {B}}=0,}
Закон электромагнитной индукции Фарадея:
-
- rotE→=−∂B→∂t,{\displaystyle \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}
Закон Ампера — Максвелла:
-
- rotB→=μj→+1c2∂E→∂t.{\displaystyle \mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}.}
Формула силы Лоренца:
-
- F→=qE→+qv→×B→,{\displaystyle {\vec {F}}=q{\vec {E}}+q\left,}
-
- Следствия из неё, такие как
Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
-
- dF→=Idl→×B→,{\displaystyle d{\vec {F}}=\left,}
- dF→=j→dV×B→,{\displaystyle d{\vec {F}}=\left,}
выражение для момента силы, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):
-
- M→=m→×B→,{\displaystyle {\vec {M}}={\vec {m}}\times {\vec {B}},}
выражение для потенциальной энергии магнитного диполя в магнитном поле:
-
- U=−m→⋅B→,{\displaystyle U=-{\vec {m}}\cdot {\vec {B}},}
- а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
- Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
-
- F→=Kqmr→r3.{\displaystyle {\vec {F}}=K{\frac {q_{m}{\vec {r}}}{r^{3}}}.}
(это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).
Выражение для плотности энергии магнитного поля
-
- w=B22μ{\displaystyle w={\frac {B^{2}}{2\mu _{0}}}}
Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).
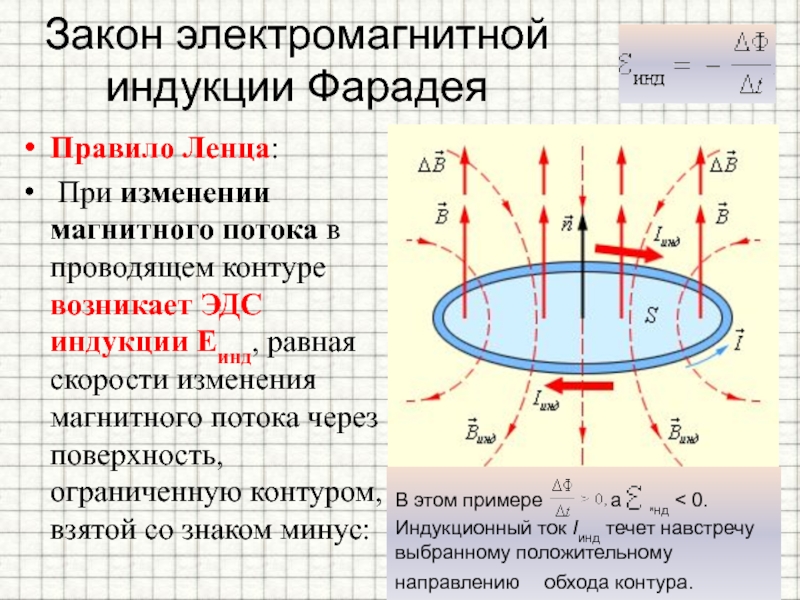
Закон электромагнитной индукции Фарадея
Данный фундаментальный закон имеет следующую формулировку: при любых изменениях магнитного потока, проходящего через проводящий контур, происходит возникновение электродвижущей силы (сокращенно ЭДС), значение которой прямо пропорционально скорости, с которой изменяется магнитный поток.
Отображением данной закономерности является следующая формула:
Ɛi = – ΔФ/Δt, где:
- Ɛi – появляющаяся в токопроводящем контуре электродвижущая сила индукции;
- ΔФ/Δt – скорость, с которой изменяется проходящий через замкнутый контур магнитный поток.
Таким образом, сила индукционного тока, образующегося в токопроводящем замкнутом контуре при воздействии на него электродвижущей силы, будет зависеть от того, с какой скоростью изменяется проходящий через него поток силовых линий магнита.
Векторная форма
В векторной форме этот закон выражается следующей формулой:
rot E= ΔB/Δt.
Согласно этой записи, напряжённость (E) электрического поля индукционного тока возрастает при увеличении скорости изменения потока B с силовыми линиями, пересекающими замкнутый контур.
Потенциальная форма
При помощи векторного потенциала закон электромагнитной индукции имеет следующую запись:
E =ΔA/Δt, где:
- Е – напряженность электрического поля, порождаемого индукционным током;
- ΔA/Δt – изменение векторного потенциала магнитного поля, проходящего через замкнутый контур, являющийся частью замкнутой цепи проводника.
Изменения в магнитосфере Земли
Характеристики земного МП меняются, в основном, вследствие того, что оно смещается относительно земного шара. Люди привыкли, что северный конец стрелы должен устремляться к северу. При обратной намагниченности диполя планеты ситуация будет противоположной. В обсерваториях фиксируются данные о состоянии МП планеты, и на их основе создаются геомагнитные карты. Они демонстрируют наличие отклонений в напряженности МП и положении силовых линий в некоторых уголках Земли. Эти явления называют магнитными аномалиями. Иногда их используют как индикаторы местоположения определенных ископаемых ресурсов.
Связь между индукцией и степенью напряженности поля широко используется в расчетах. Она позволяет вывести выражения для нахождения значения индукции в проводниках разных форм, сделанных из материалов с различными показателями магнитной проницаемости.
Паразитная индукция и тепловые потери
Рассмотренные явления могут применяться с пользой для разогрева кухонной посуды или плавки различных материалов. Однако в трансформаторах и электродвигателях паразитные вихревые индукционные токи – это негативное явление. Кроме прямых энергетических потерь, увеличивается вероятность аварийных ситуаций. При слишком высокой температуре повреждается изоляция.
Расслоение электромагнита
Уменьшают негативные проявления с помощью особых «наборных» конструкций. Если объединить несколько пластин, обеспечивается взаимная компенсация полей.
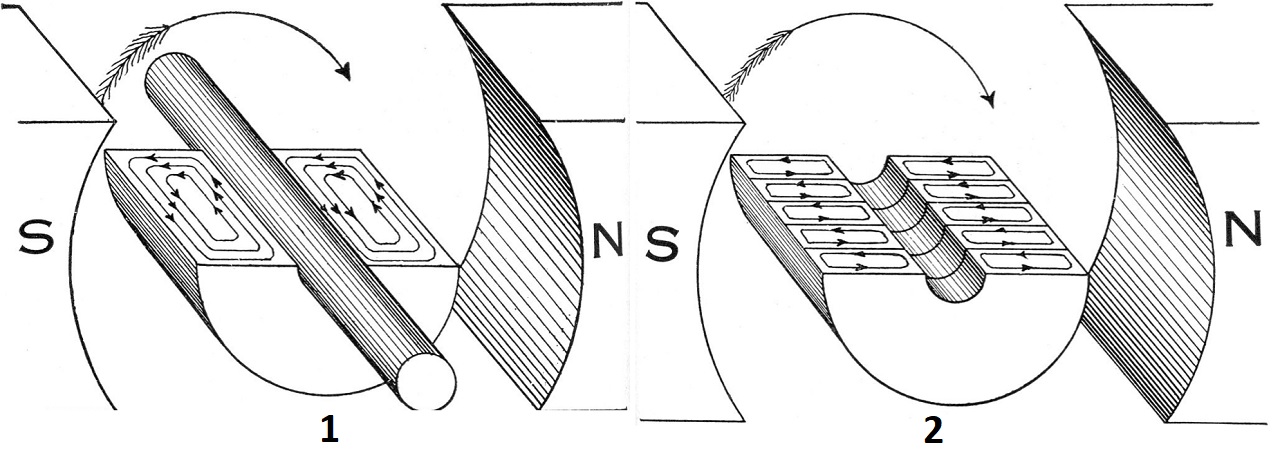 Принцип конструкции из нескольких слоев
Принцип конструкции из нескольких слоев
При правильном расчете потери уменьшают (2) до 1-2% от уровня, который создает цельный аналог (1).
Паразитные потери в катушках индуктивности
Размеры проводника также имеют значение. Крупные элементы образуют паразитные токи, так как в определенном положении распределение линий магнитного поля неравномерно.
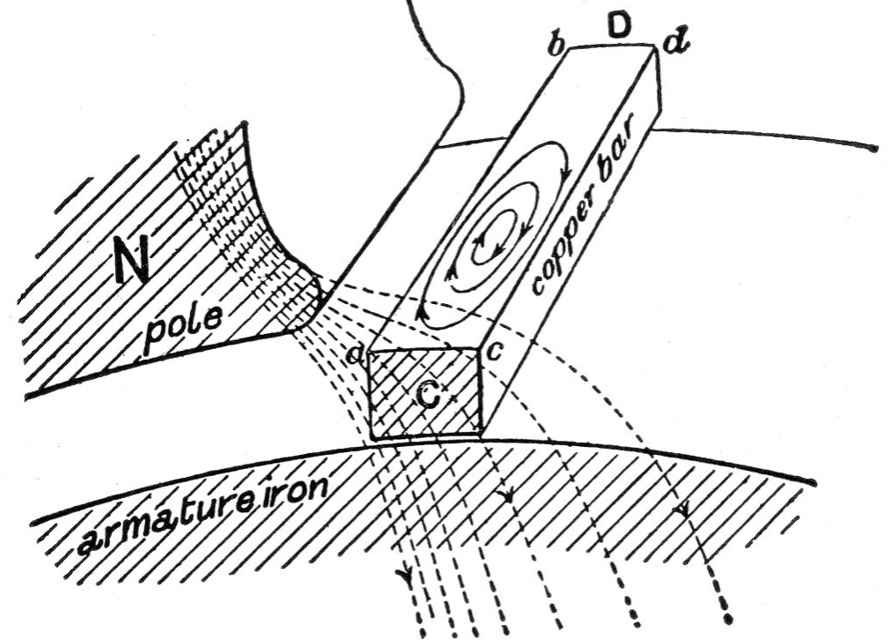 Пояснение к появлению в катушке паразитных токов
Пояснение к появлению в катушке паразитных токов
На рисунке схематично показаны различные силовые характеристики поля для участков по линиям a-b и c-d, соответственно. При уменьшении размеров проводника снижаются энергетические потери. В некоторых устройствах этот параметр определят класс энергетической эффективности.
Физический смысл магнитной индукции
Прежде, чем перейти к рассмотрению формулы магнитной индукции, нужно выяснить, чем объясняется возникновение самого явления в системе. Соленоид не является плоским элементом и включает в себя спираль из проводника (металла). При отсутствии воздействующих на него магнитных явлений находящиеся в кристаллической решетке материала спирали электрозаряды ведут себя статично. Когда в соленоиде движется постоянный магнитный элемент, формирующий поле, под его влиянием движутся и заряженные частицы, тогда в индуктивном элементе появляется электрический ток, сила которого определяется характеристиками магнитного и спирального элемента и тем, как быстро происходит движение.
Важно! Имеющие одинаковую ориентацию поля суммируются, образуя общее поле. Когда передвижение заряженных частиц в соленоиде прекращается, сердечник перестает проявлять магнитные характеристики, если он выполнен из мягкого металла (к стальным изделиям это правило не относится)
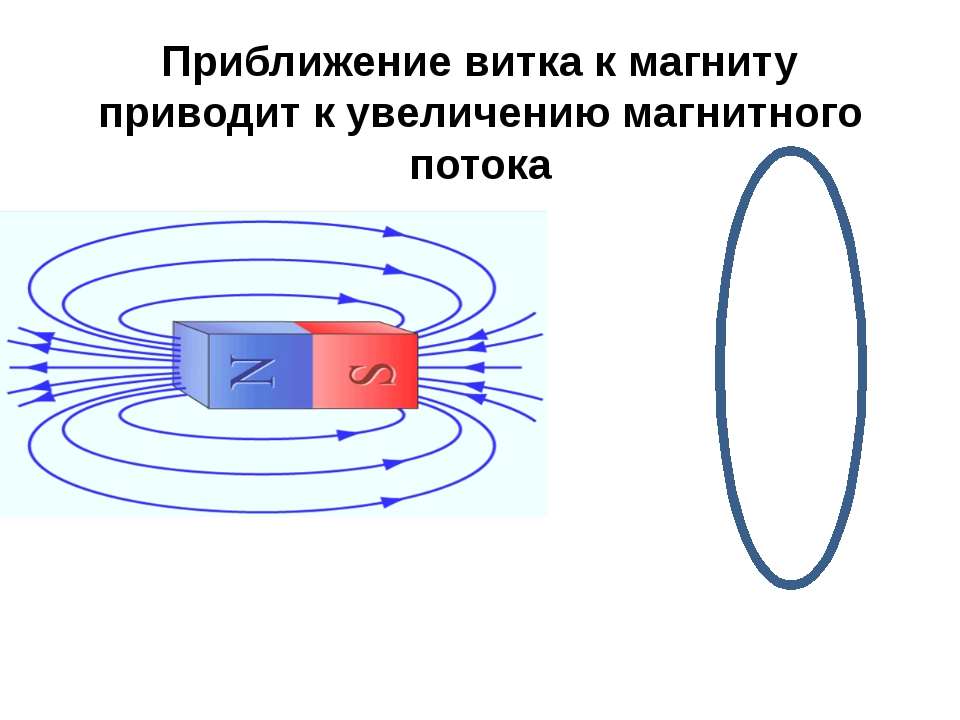
Взаимодействие магнита с контуром
В качестве наглядного примера взаимодействия магнита и контура в сделанную из медного провода катушку помещают магнит. Если магнит медленно вставлять внутрь катушки, происходит постепенное увеличение пересекающего ее витки создаваемого магнитом потока. Появляющееся вследствие такой манипуляции упорядоченное движение частиц в катушке будет направлено по часовой стрелке, создавая собственное магнитное поле, ослабляющее поле магнита, отталкивая его тем самым от катушки.
Если магнит отдаляют от контура, его поток уменьшается, а заряженные частицы начинают двигаться против часовой стрелки, вследствие чего возникающая совокупность силовых магнитных линий будет притягивать магнит.
На заметку. В случае с незамкнутым (открытым) контуром: металлическим или алюминиевым кольцом, имеющим прорезь; катушкой, витки которой не замкнуты через амперметр, источник питания, данная закономерность, как и правило Ленца, не работает.
Направление вектора МИ
Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.
Линии магнитной индукции
Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.
Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали
В некоторых случаях, чтобы найти направление, применяют правило правой руки.
Наглядное отображение линий МИ
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.
С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.
Заказать решение ТОЭ
- Метрология Электрические измерения
- Пигарев А.Ю. РГЗ по электротехнике и электронике в Multisim
-
Теория линейных электрических цепей ТЛЭЦ
-
—
Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: задание на контрольные работы № 1 и 2 с методическими указаниями для студентов IV курса специальности Автоматика, телемеханика и связь на железнодорожном транспорте-
—
Контрольная работа №1 -
—
Контрольная работа №2
-
—
-
—
-
Электротехника и основы электроники
-
—
Электротехника и основы электроники: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений / Соколов Б.П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил-
—
Контрольная работа № 1 Электрические цепи -
—
Контрольная работа № 2 Трансформаторы и электрические машины -
—
Контрольная работа № 3 Основы электроники
-
—
-
—
-
Теоретические основы электротехники ТОЭ
-
—
Артеменко Ю.П., Сапожникова Н.М. Теоретические основы электротехники: Пособие по выполнению курсовой работы МГТУ ГА 2009 -
—
Переходные процессы Переходные процессы в электрических цепях -
—
Теоретические основы электротехники Методические указания и контрольные задания для студентов технических специальностей вузов-
—
Задание 1 Линейные электрические цепи постоянного и синусоидального тока-
—
Задача 1.1 Линейные электрические цепи постоянного тока -
—
Задача 1.2 Линейные электрические цепи синусоидального тока
-
—
-
—
Задание 2 Четырехполюсники, трехфазные цепи, периодические несинусоидальные токи, электрические фильтры, цепи с управляемыми источниками
-
—
-
—
Теоретические основы электротехники сб. заданий Р.Я. Сулейманов Т.А. Никитина Екатеринбург УрГУПС 2010 -
—
Трехфазные цепи. Расчет трехфазных цепей -
—
УГТУ-УПИ Решение ТОЭ Билеты по ТОЭ -
—
Электромагнитное поле Электростатическое поле Электростатическое поле постоянного тока в проводящей среде Магнитное поле постоянного тока
-
—
Вращающаяся катушка
Обеспечить оптимальное расположение функциональных компонентов при одновременном перемещении сложно, если применять представленный в примере прямой провод. Однако согнув рамку, можно получить простейший генератор электроэнергии. Максимальный эффект обеспечивает увеличение количества проводников на единицу рабочего объема. Соответствующая отмеченным параметрам конструкция – катушка, типичный элемент современного генератора переменного тока.
Для оценки магнитного потока (F) можно применить формулу:
F = B * S * cosα,
где S – площадь рассматриваемой рабочей поверхности.
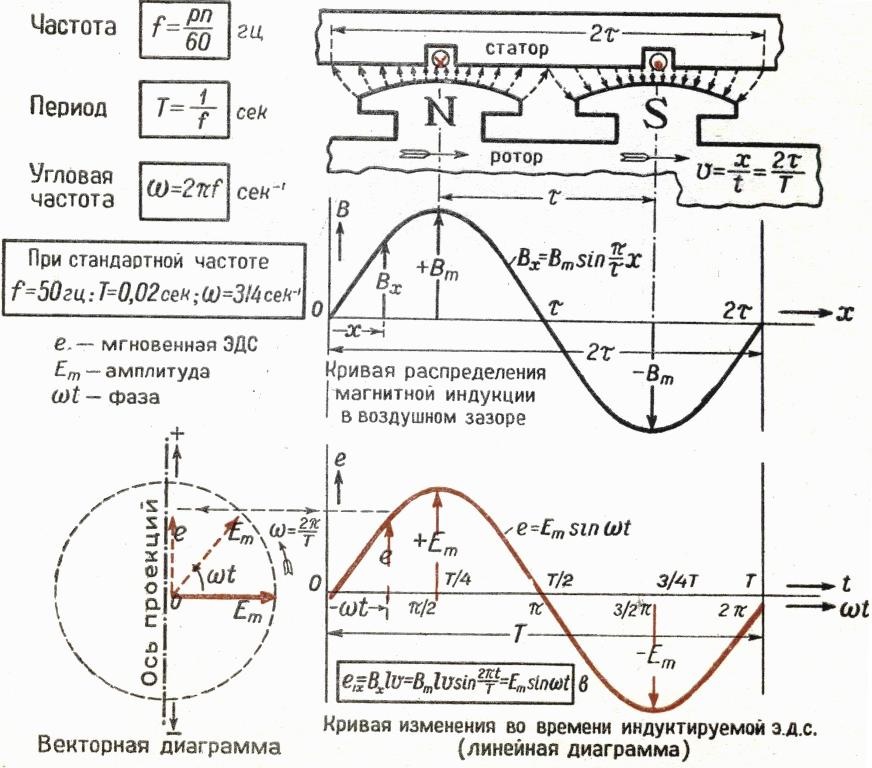 Формулы для расчета и особенности конструкции типичного генератора
Формулы для расчета и особенности конструкции типичного генератора
Пояснение. При равномерном вращении ротора происходит соответствующее циклическое синусоидальное изменение магнитного потока. Аналогичным образом меняется амплитуда выходного сигнала. Из рисунка понятно, что определенное значение имеет величина зазора между основными функциональными компонентами конструкции.
Явление электромагнитной индукции
Первые опыты в соответствующей области делал датчанин Эрстед. В 1821 году он обнаружил отклонение стрелки магнитного компаса, поднесенной к проводнику с электрическим током. Однако смысл отмеченных проявлений был сформулирован позднее.
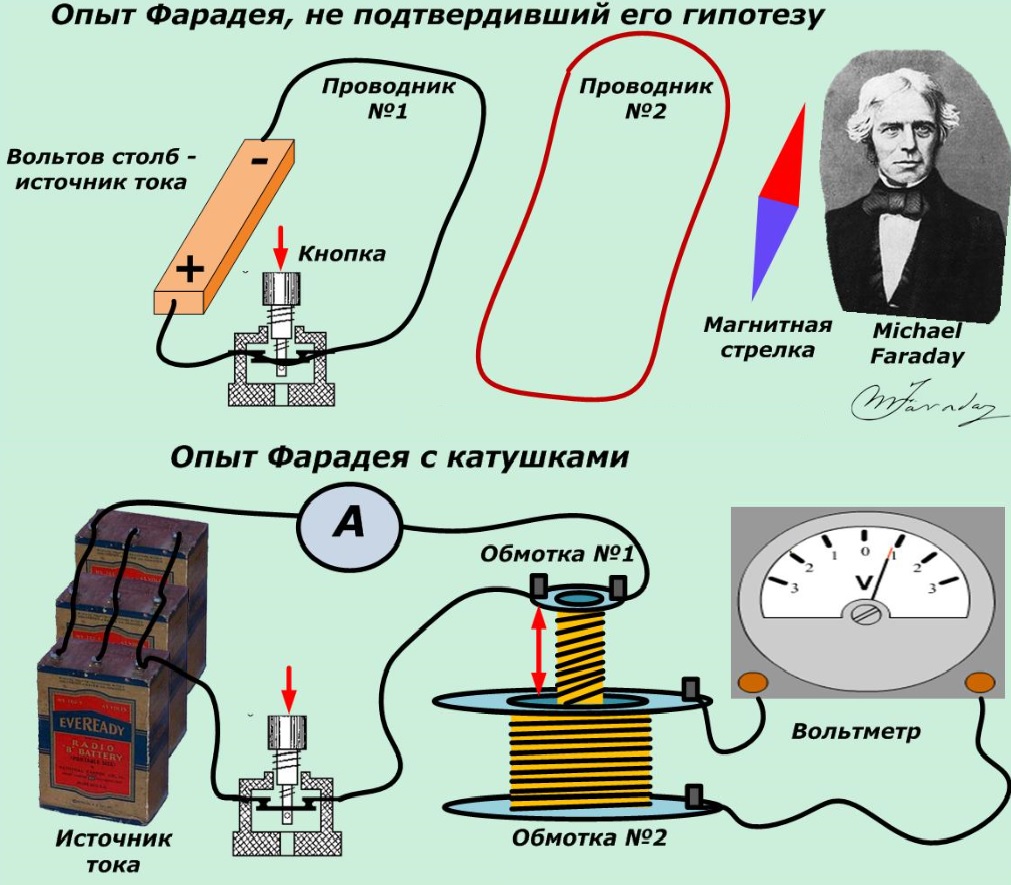 Схемы опытов
Схемы опытов
Эксперименты заинтересовали Фарадея, который предположил возможность создания устройства для генерации энергии. В первой установке два проводника ученый разместил на небольшом расстоянии. Через один – с помощью вольтова столба подавал ток. Однако стрелка компаса, установленная возле второй цепи, никак не реагировала на такие действия.
К сведению. Более чувствительный прибор смог бы зарегистрировать ток в контрольном проводнике. Фактически эта схема является прообразом радио тракта. На этих принципах, в частности, функционируют беспроводные системы передачи данных Wi-Fi и линии мобильной связи.
В нижней части рисунка изображен второй (успешный) опыт Фарадея. Две катушки обеспечивают более сильное взаимодействие полей, поэтому измерение не вызвало больших затруднений. Прибор показал изменение напряжения в контрольном контуре.
Данное явление наблюдалось при следующих действиях:
- включение/выключение источника тока;
- перемещение катушек;
- изменение скорости движения функциональных компонентов.
В 1831 году экспериментатор опубликовал вывод. Эта формулировка используется для определения базовых условий и зависимостей: «В замкнутом контуре изменяющийся магнитный поток создает электродвижущую силу». Отдельно были отмечены следующие особенности:
- отрицательное значение ЭДС;
- зависимость разницы потенциалов от скорости, с которой изменяется магнитное воздействие.
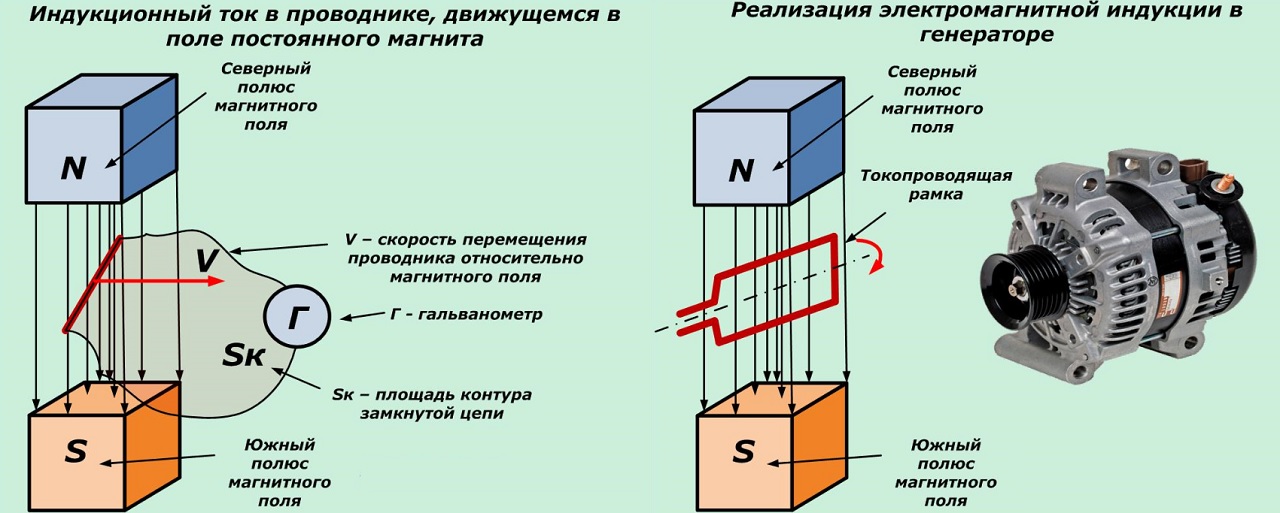 Несложно догадаться о том, что вращением рамки в магнитном поле обеспечивают генерацию электроэнергии
Несложно догадаться о том, что вращением рамки в магнитном поле обеспечивают генерацию электроэнергии
Опыты Фарадея стали основой для создания других известных изделий:
- электродвигателей;
- индукционных варочных панелей (плавильных печей);
- трансформаторов;
- измерительных приборов.
Магнитосфера Земли
Магнитосферой называется пространство, прилежащее к небесному телу и обладающее особыми свойствами, которые определяются взаимодействием МП планеты с заряженными частицами из внешнего пространства. Для Земли диаметр этой сферы составляет более 90 тысяч километров.
Наша планета обладает основным и переменным магнитными полями. Первое формируется электротоками, образующимися на плотном ядре вследствие разницы температур. Второе образуется из-за действия внешних сил (электротоков в атмосфере) и отличается большой нестабильностью. С ним связаны такие явления, как магнитные бури и северное сияние.
Полевое пространство Земли может быть описано рядом показателей, например, его напряженность описывает силу и привязана к географической широте. Магнитное склонение показывает разницу между меридианом (с вектором, направленным на север) и соответствующей позицией магнитной стрелки.