- Как вычислить общее сопротивление цепи
- Метод 1 Последовательное соединение
- Метод 2 Параллельное соединение
- Метод 3 Комбинированное соединение
- Метод 4 Формулы, включающие мощность
- Что такое резистор и для чего он нужен
- Параллельное соединение резисторов
- Теория и законы параллельного соединения
- Примеры расчета параллельного соединения сопротивлений
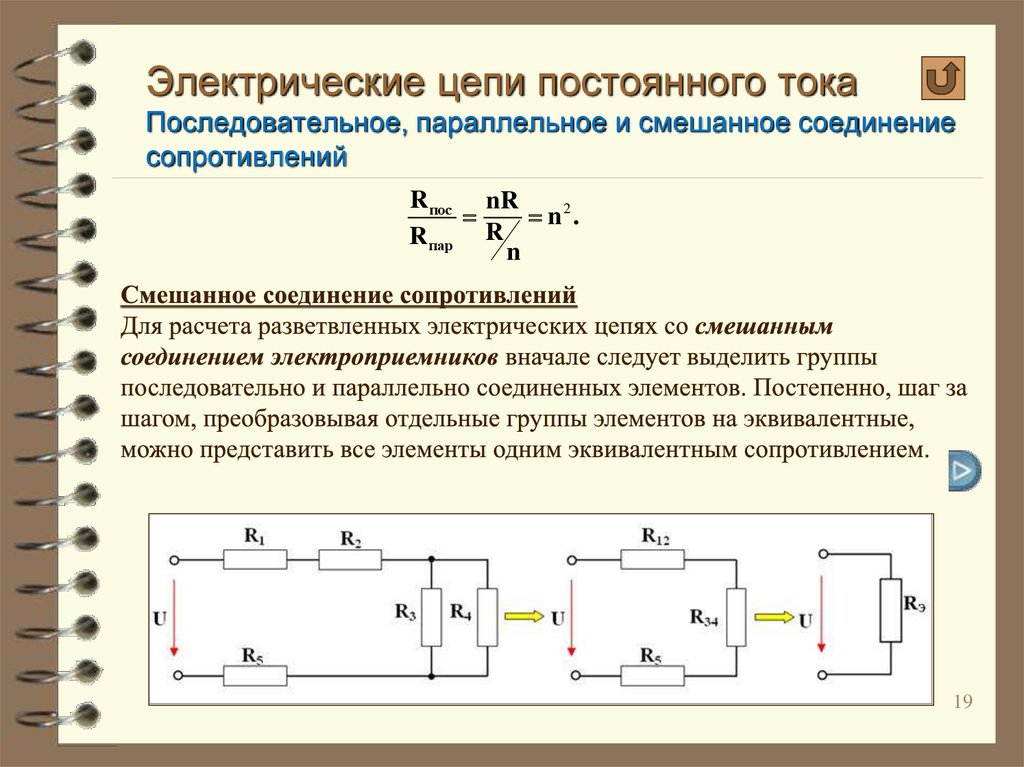
- Смешанное соединение
- Как определить формулой общее сопротивление цепи
- Реактивное внутреннее сопротивление
- Расчёт
- Последовательное соединение резисторов
- Параллельное соединение резисторов
- Смешанное соединение резисторов
- Последовательное соединение сопротивлений
- Теоретическая часть
- Примеры расчета
- От чего зависит сопротивление резистора
- Как зависит от температуры
- От других параметров
- Метод — эквивалентное сопротивление
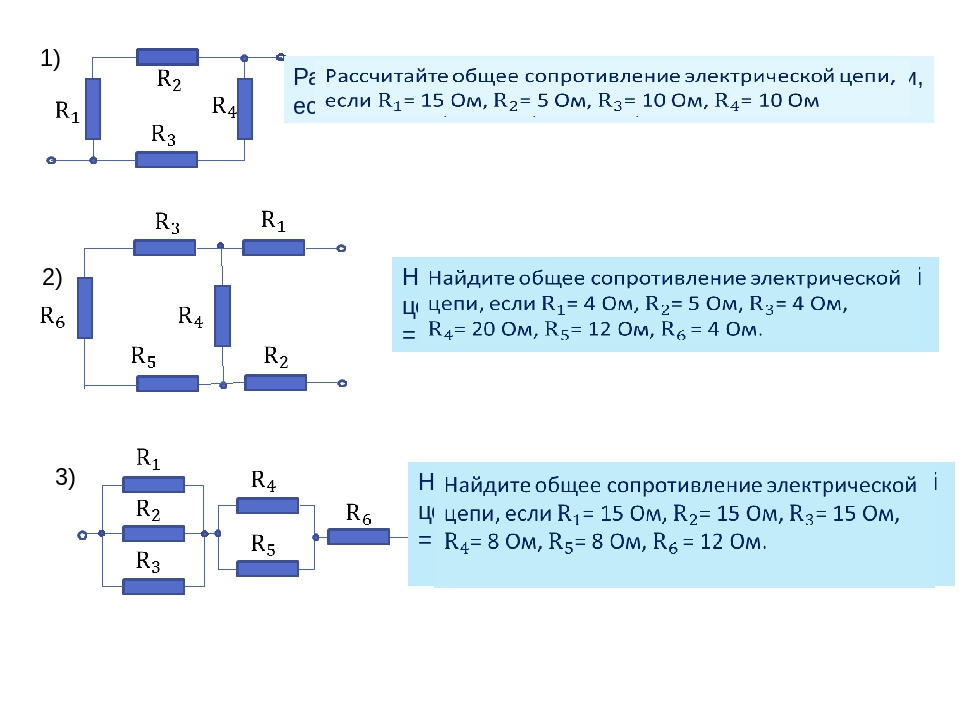
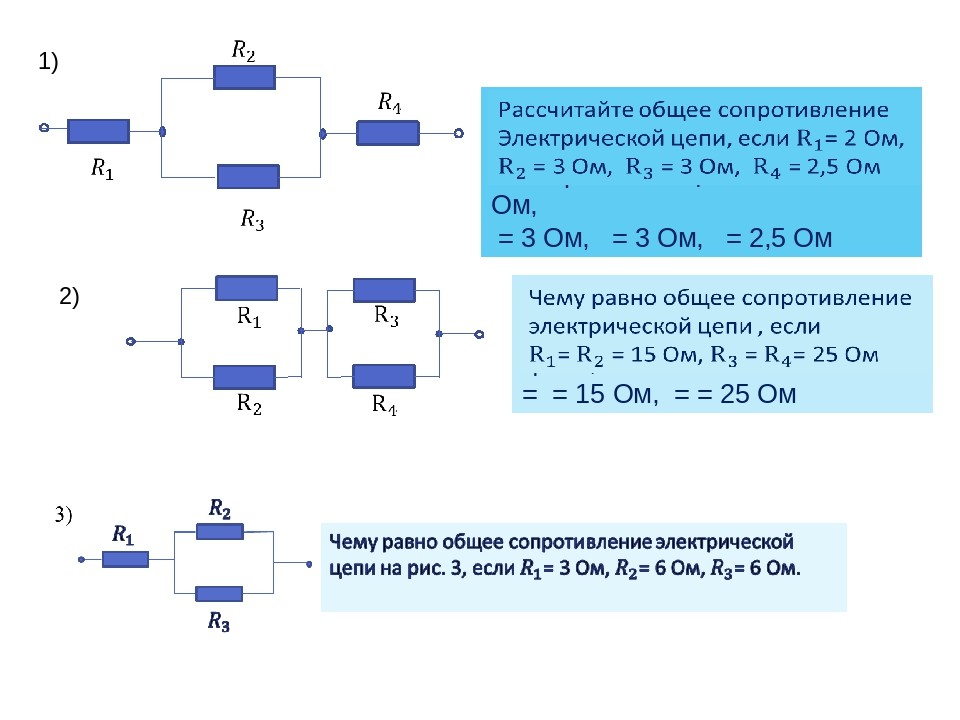
- Практические задания:
- Основные понятия
- Сила и напряжение
- Сопротивление проводников
- Параллельное соединение резисторов.
- Как найти сопротивление резистора в цепи
- При последовательном соединении
- Могут ли быть погрешности и какие
- Последовательное подключение
- Теоретическая часть
- Примеры расчета
- Общее сопротивление Rобщ
- Заказать решение ТОЭ
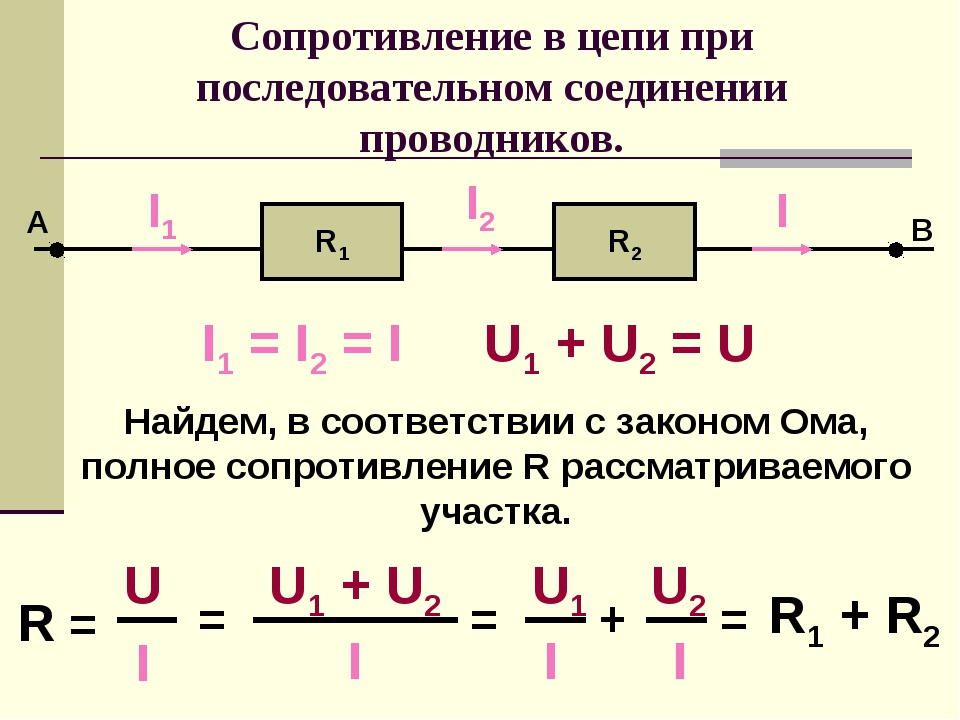
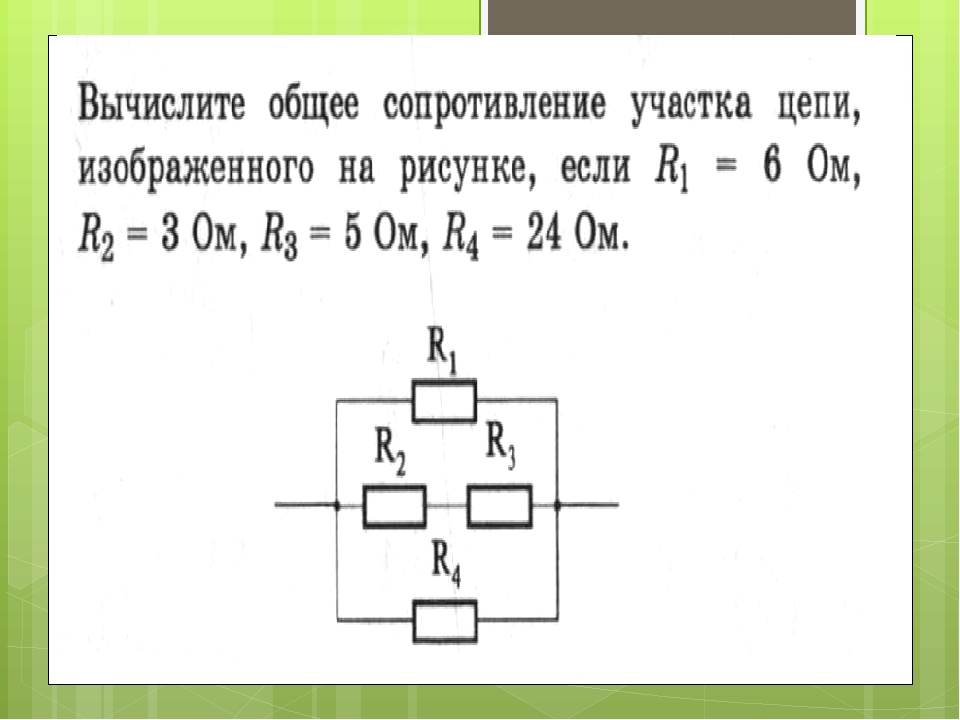
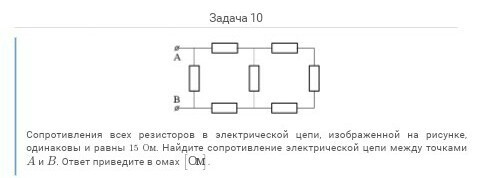
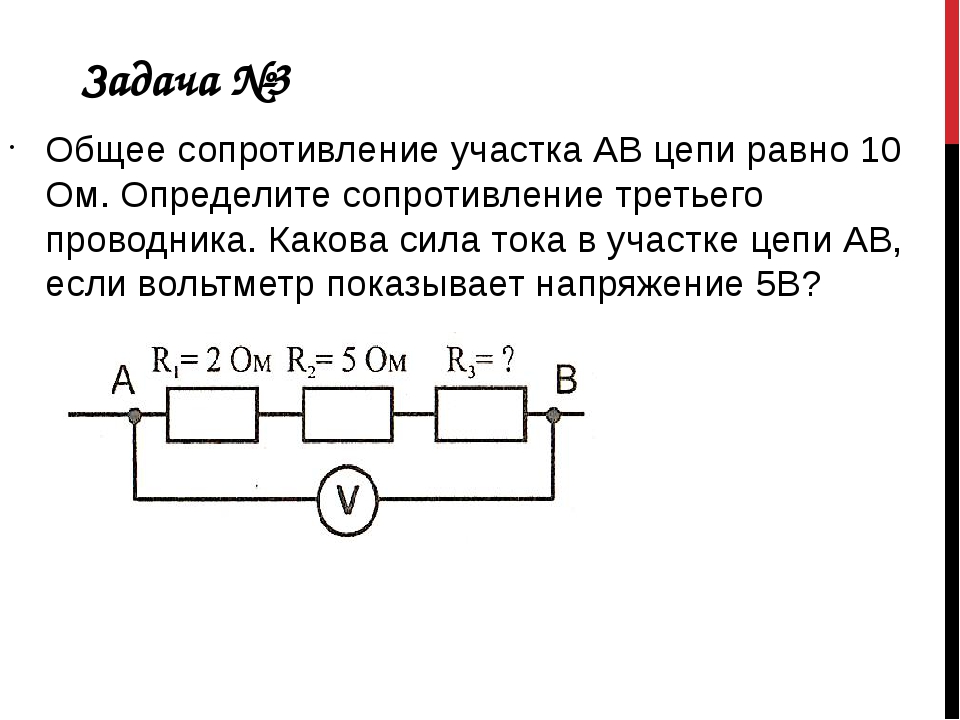
Как вычислить общее сопротивление цепи
Для расчетов используют представленные выше правила, формулы, проверочные действия. Рекомендуется сначала изобразить схему в упрощенном виде, с комплексным объединением отдельных участков. Далее вычисляют эквивалентные сопротивления соответствующих групп. При необходимости можно определить токи в цепях, находить значения напряжений в контрольных точках.
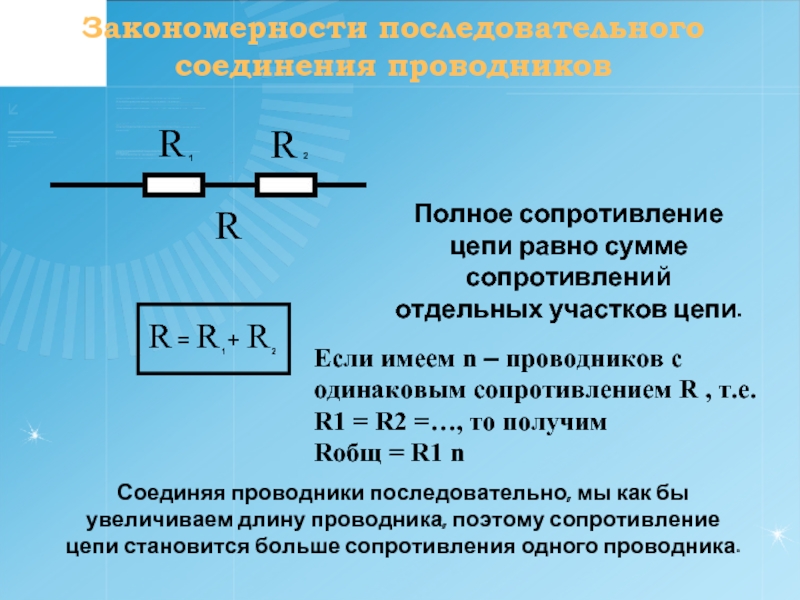
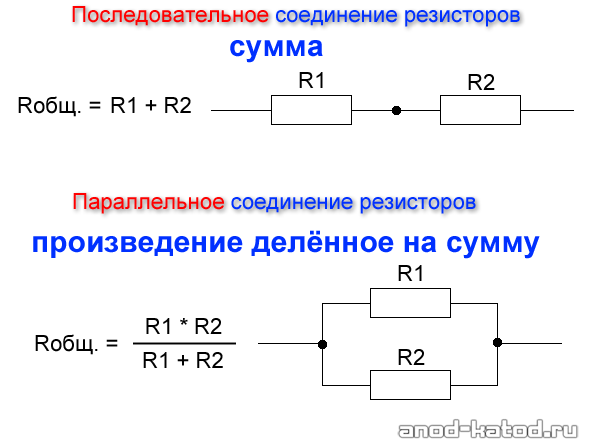
Метод 1 Последовательное соединение
Для таких соединений применяют представленное выше простое суммирование:
Rобщ = R1 + R2 + … + Rn.
Ток в замкнутой цепи не изменяется. Проверка при подключении мультиметра в любой разрыв покажет одно и то же значение. Вместе с тем на каждом резисторе при разных номиналах элементов будет различное падение напряжения. В соответствии со вторым постулатом Кирхгофа результат вычислений проверяют сложением:
Uакб = U1 + U2 + Un.
К сведению. С помощью приведенной схемы нетрудно рассчитать делитель напряжения на определенный уровень при известных рабочих параметрах источника питания постоянного тока.
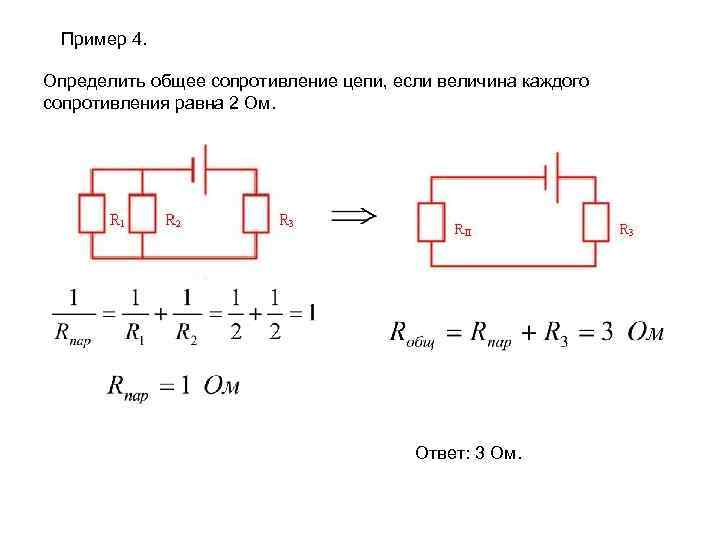
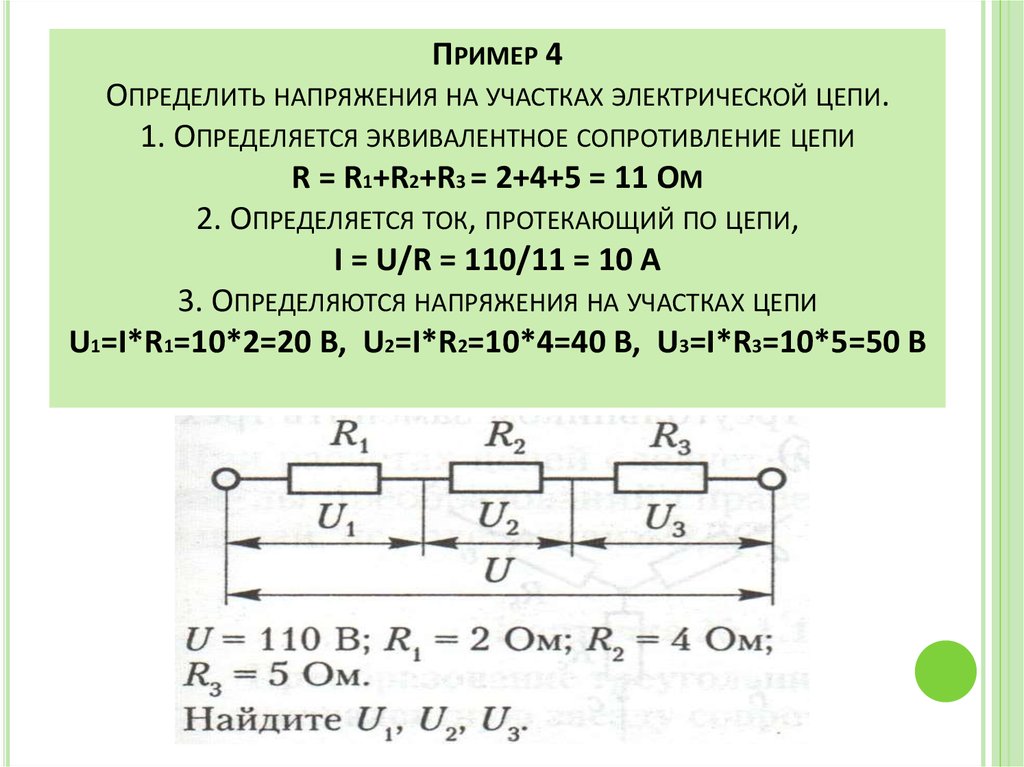
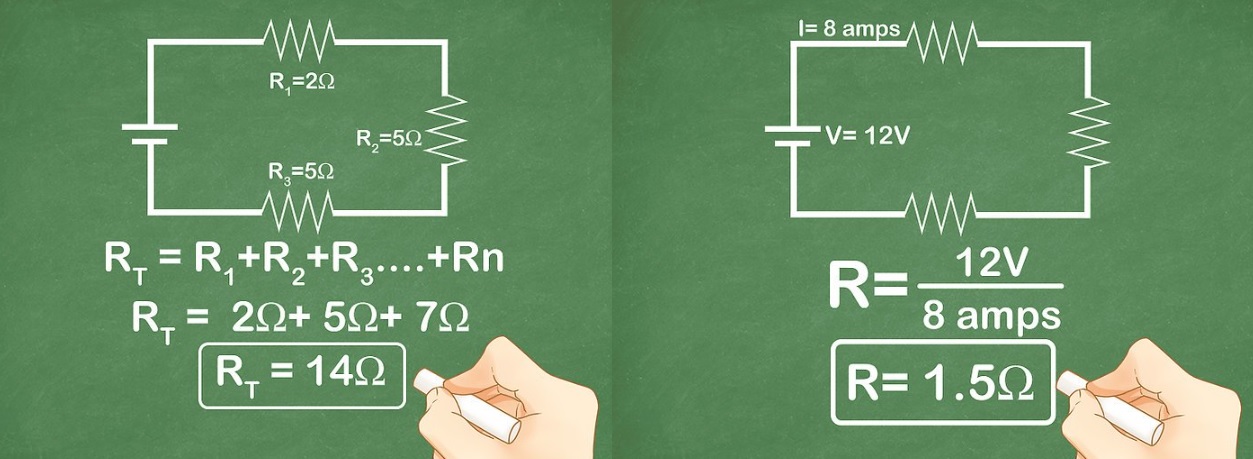 Пример вычислений для последовательного соединения
Пример вычислений для последовательного соединения
Метод 2 Параллельное соединение
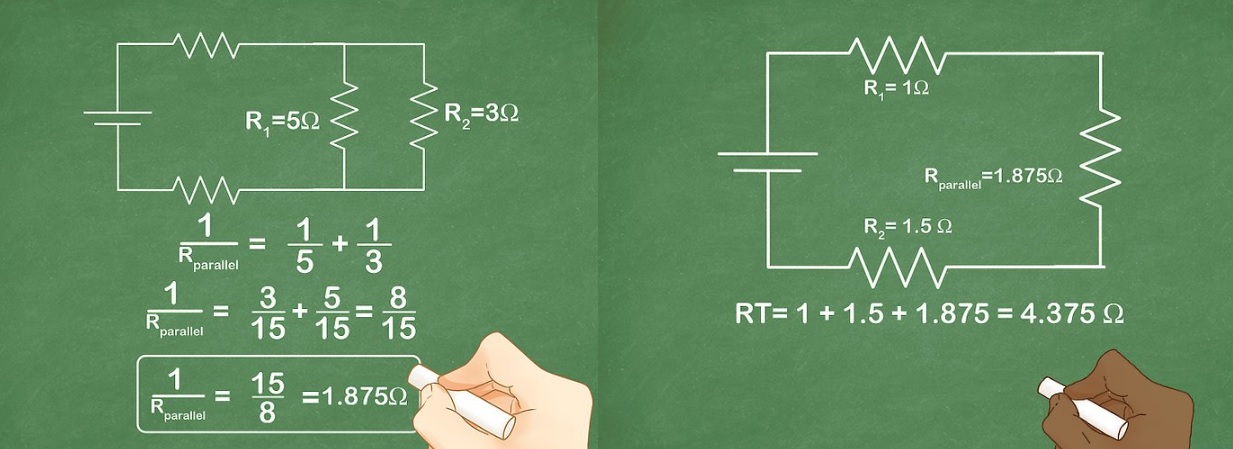
В этом варианте соединения удобно оперировать с обратным сопротивлению параметром – проводимостью. Впрочем, допустимо применение и такой исходной формулы:
1/Rобщ = 1/R1 + 1/R2 = 1/(1/R1 + 1/R2) = R1*R2/R1 + R2.
В узле на входе ток распределяется по разным цепям пропорционально номиналам соответствующих резисторов. На выходе происходит обратное преобразование. Проверку вычислений выполняют по принципам первого постулата Кирхгофа.
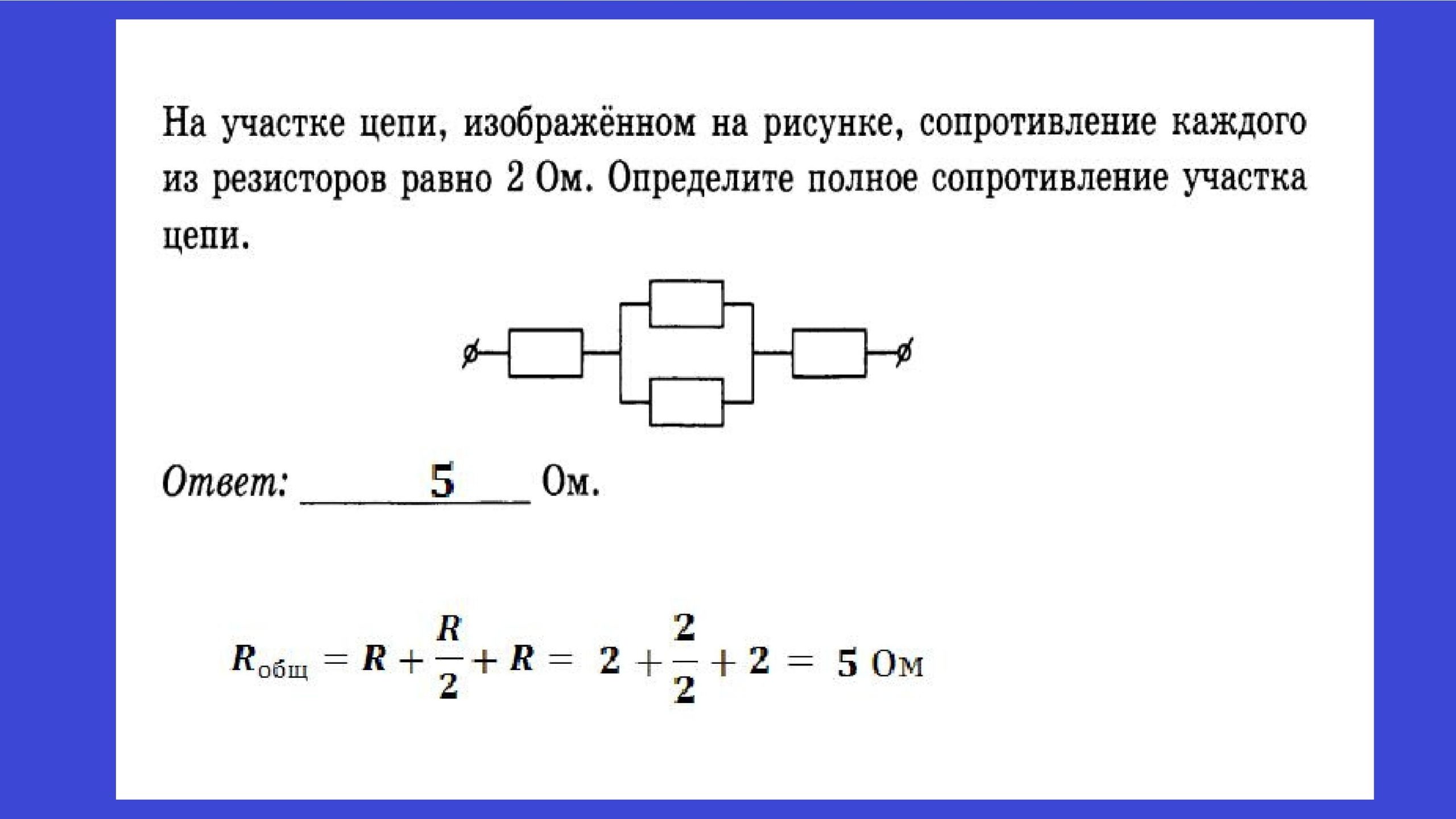
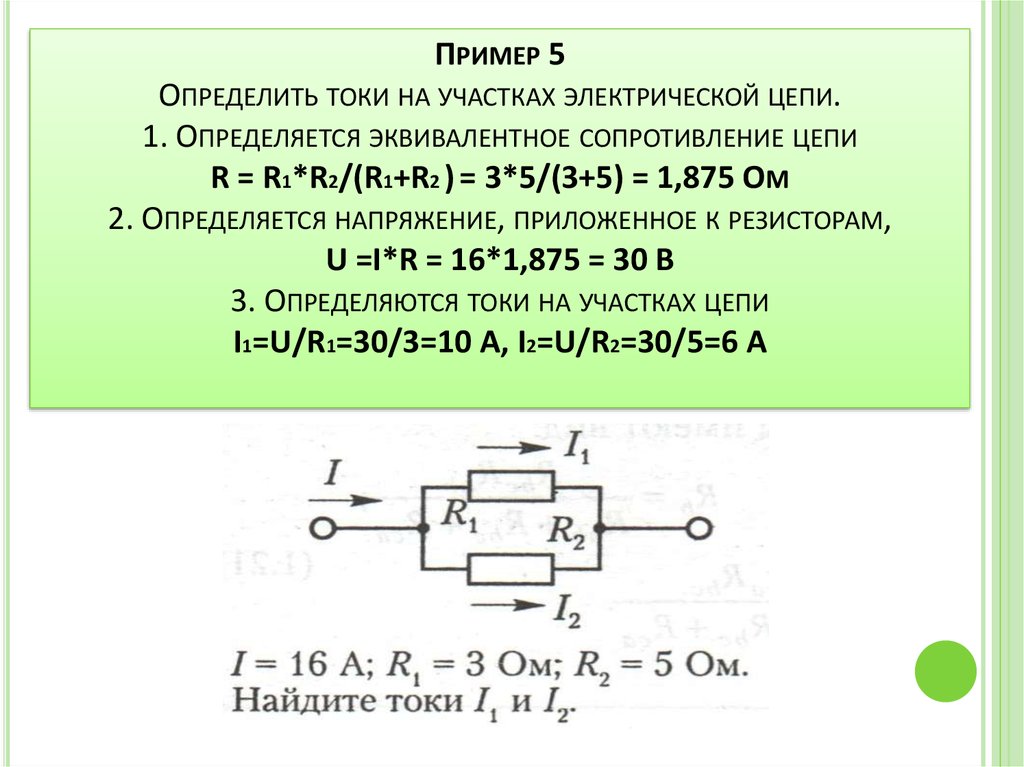
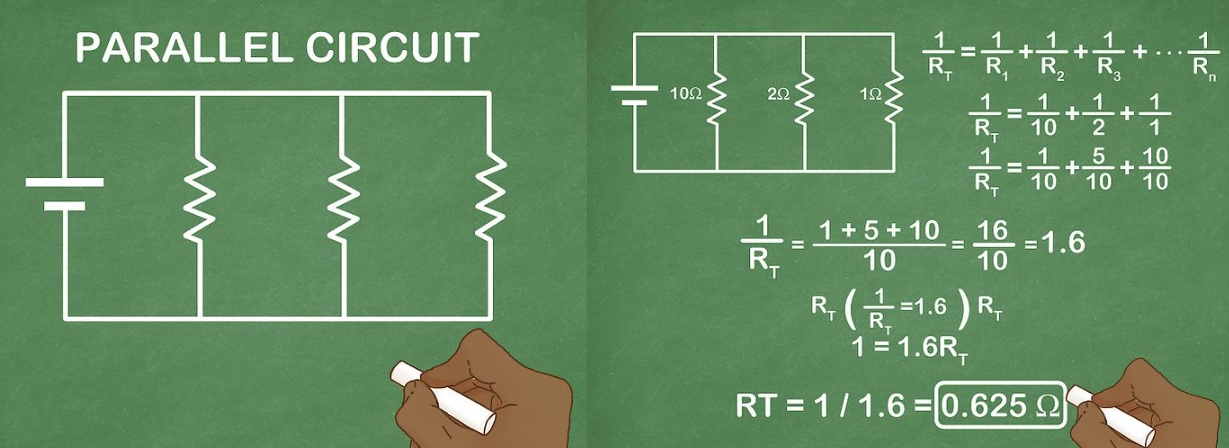 Формулы и пример для параллельного соединения
Формулы и пример для параллельного соединения
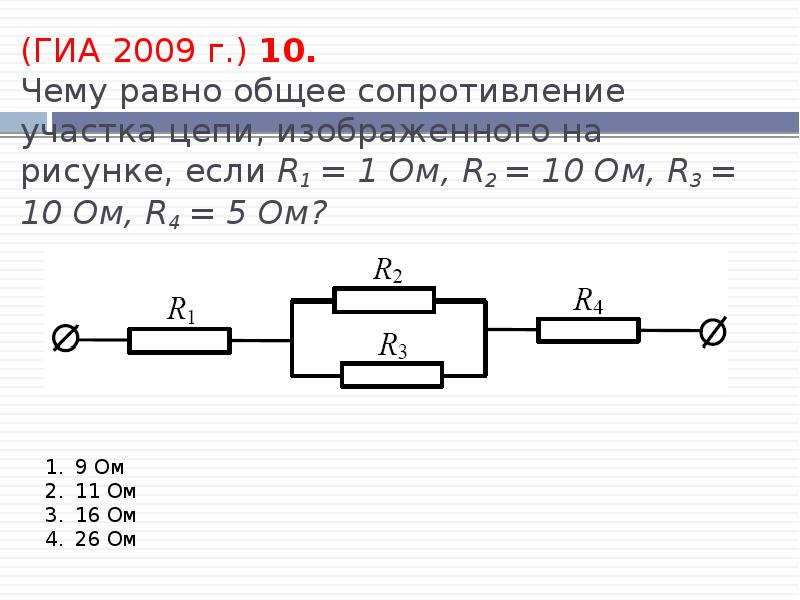
Метод 3 Комбинированное соединение
Сложные схемы упрощают. Отдельно рассчитывают параллельный участок. Далее создают неразветвленный контур из последовательных элементов.
 Сложный расчет
Сложный расчет
При необходимости можно трансформировать схему из соединения резисторов «треугольником» в «звезду» или обратно. Ниже приведены формулы для расчета эквивалентных сопротивлений в цепях после преобразования.
 Перевод «звезды» в «треугольник»
Перевод «звезды» в «треугольник»
Метод 4 Формулы, включающие мощность
Каков будет результат, узнать несложно с помощью любой из подходящих формул:
P = I2 *R = U2/ R.
Исходные параметры берут из предварительных расчетов либо определяют измерением. Можно использовать схемы вычислений с токами в цепях или напряжением на отдельных резисторах (группах последовательно соединенных элементов).
Что такое резистор и для чего он нужен
Резистор — это радиоэлемент, который увеличивает сопротивление цепи. Ставят его обычно для того, чтобы понизить/ограничить напряжение или ток. Есть сопротивления постоянные и переменные.
Например, светодиоды требуют небольшого тока, иначе перегревается и быстро выходит из строя. Чтобы ограничить ток, перед светодиодом поставьте сопротивление. Ток в цепи станет меньше.
Для чего нужны резисторы: для подстройки параметров питания
Постоянные сопротивления — это те, которые не меняют своего номинала в процессе работы. Если это и происходит, то считается выходом из строя.

Так выглядят переменные и постоянные резисторы
Переменные резисторы, наоборот, отличаются тем, что их сопротивление можно изменять. Они имеют бегунок или поворотную ручку, при помощи которых и изменяется номинал. На основе таких устройств делают регуляторы. Например, регулятор громкости, накала греющего элемента и т.д.
Параллельное соединение резисторов
Параллельное соединение — это когда входы нескольких деталей соединяются в одной точке. Точно так же — в одну точку — соединяют их выходы.
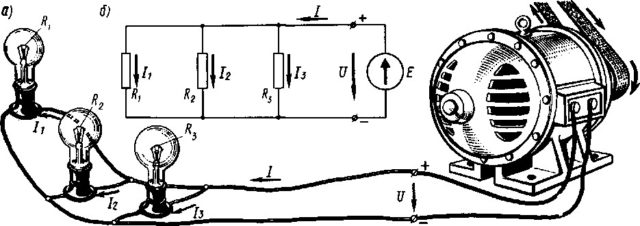
Так выглядит параллельное соединение на схеме и в реальности
Теория и законы параллельного соединения
Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение. То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение.
Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
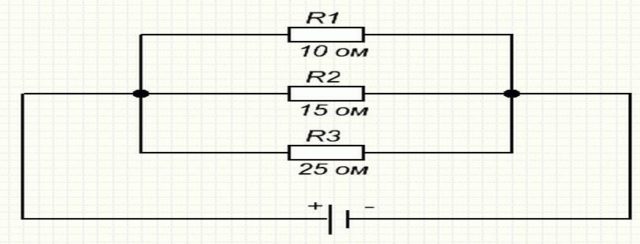
Так выглядит параллельное соединение резисторов на схеме
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле:
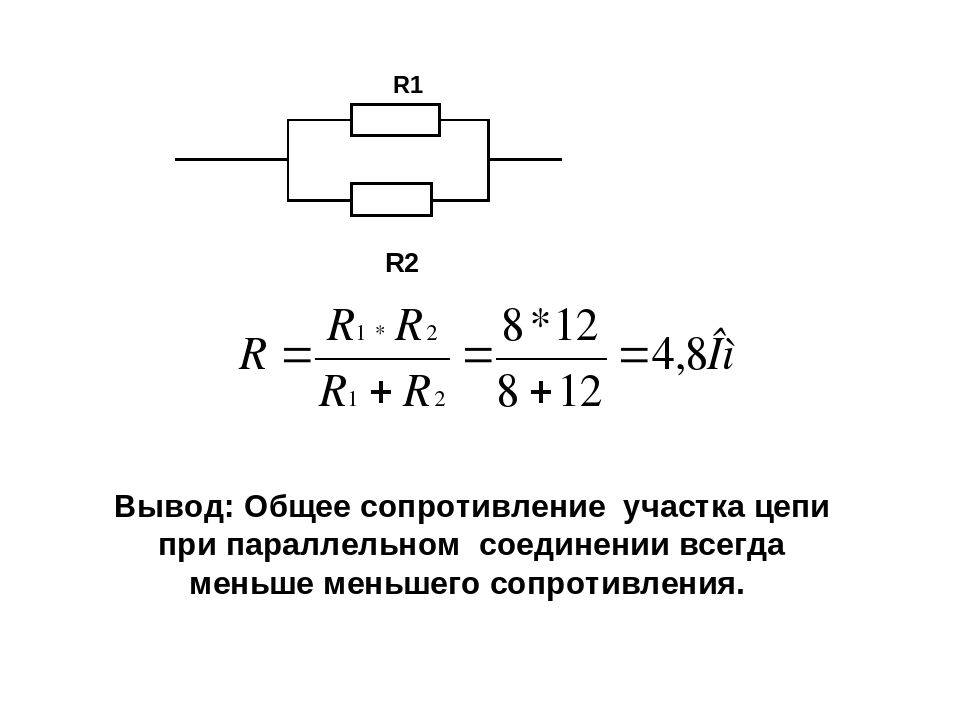
Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
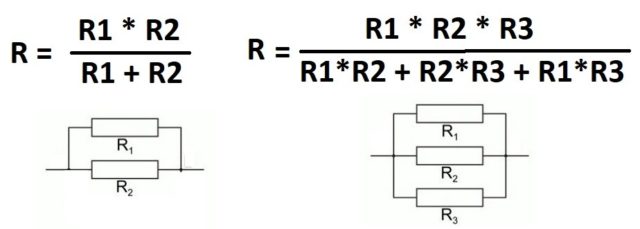
Формулы расчета сопротивления при параллельном подключении двух и трех резисторов
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала.
Примеры расчета параллельного соединения сопротивлений
Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
- Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
- Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.
Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.
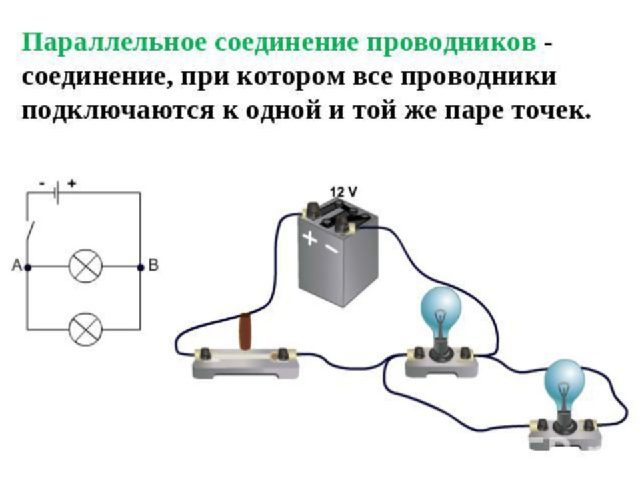
Еще один пример с лампочками
При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее. Но картина не отличается:
- Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом.
- Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом.
Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
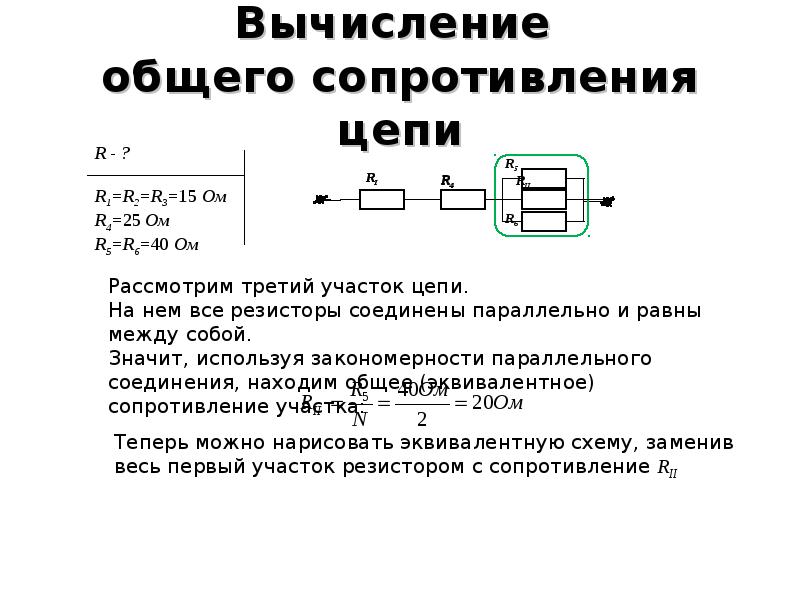
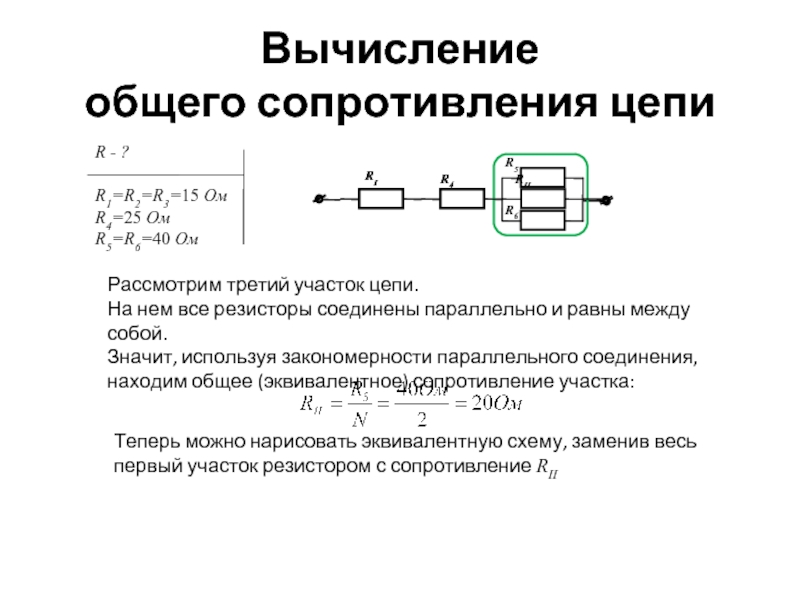
Смешанное соединение
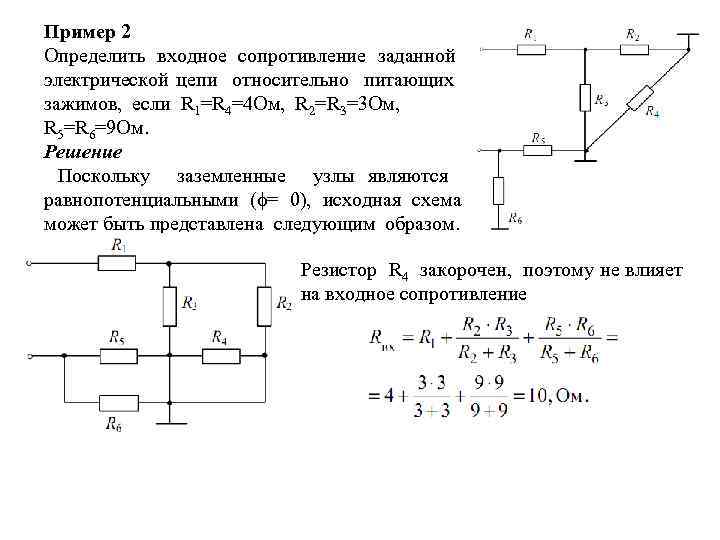
Как быть, если в схеме есть и параллельное, и последовательное соединение резисторов? В таком случае считают общее сопротивление по участкам. Можно при этом перерисовывать схему, заменяя составные сопротивления на один «прямоугольник», но проставляя над ним высчитанный результат.
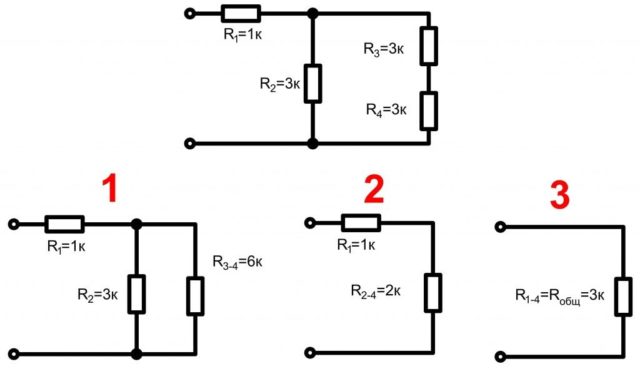
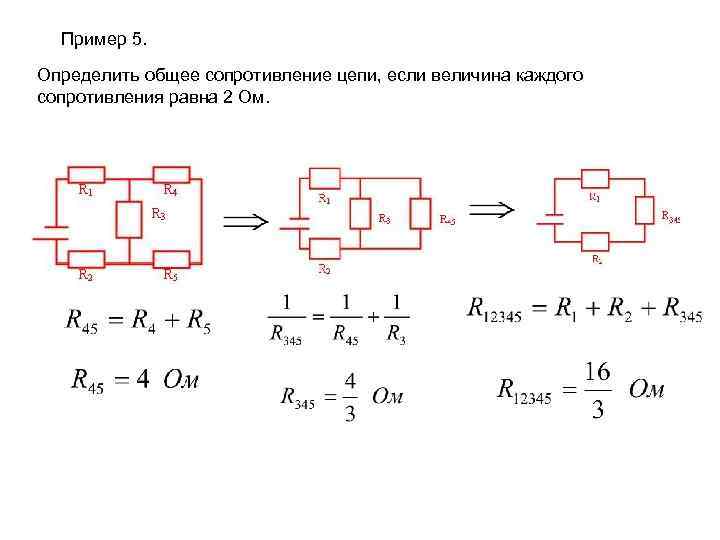
Пример расчета сопротивления при смешанном соединении резисторов. Рассматриваем исходную схему как совокупность параллельных и последовательных соединений
Шаг 1. Нашли общее сопротивление последовательно соединенных резисторов R3 и R4:
R3-4 = 3 кОм + 3 кОм = 6 кОм;
Шаг 2. Рассчитали сопротивление параллельно соединенных резисторов R2 и R3-4:
R2-4 = 3 кОм * 6 кОм / (3 кОм + 6 кОм) = 18 кОм/9 кОм = 2 кОм;
Шаг 3. Рассчитали общее сопротивление последовательно соединенных резисторов R1 и R2-4:
R1-4 = R1 + R2-4 = 1 кОм + 2 кОм = 3 кОм.
Как определить формулой общее сопротивление цепи
Из закона Ома исходит то, что общее сопротивление равно общему напряжению, деленному на общую силу тока в цепи. При параллельном подключении напряжение, как уже было сказано, равно везде, поэтому необходимо узнать его значение на любом участке цепи. С током все сложнее, так как на каждой ветке его значение свое и зависит от конкретного R.
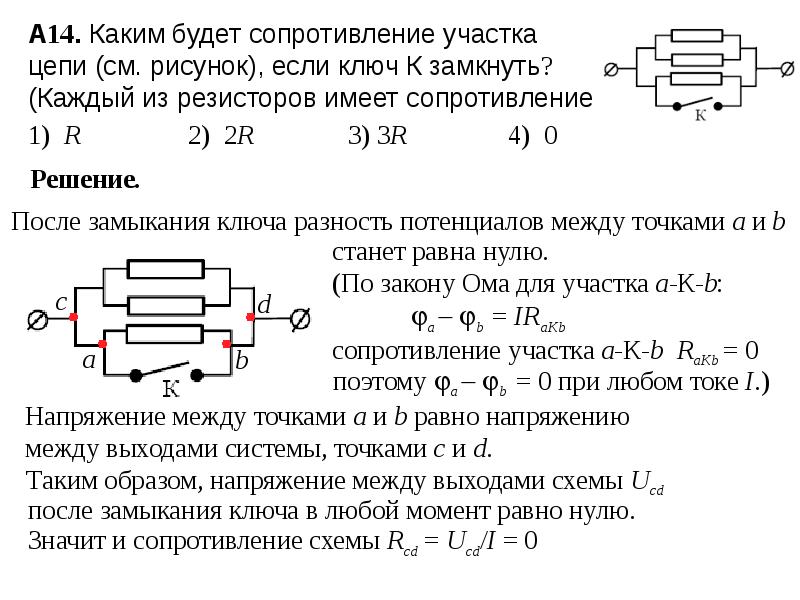
Также необходимо помнить, что могут быть параллельные подключения с нулевым значением R. Если в какой-либо ветке нет резистора или другого подобного элемента, но весь ток будет течь через нее и все общее значение для цепи станет нулевым. На практике это случается при выходе резистора из строя или при замыкании. Такая ситуация может навредить другим элементам из-за большой силы тока.
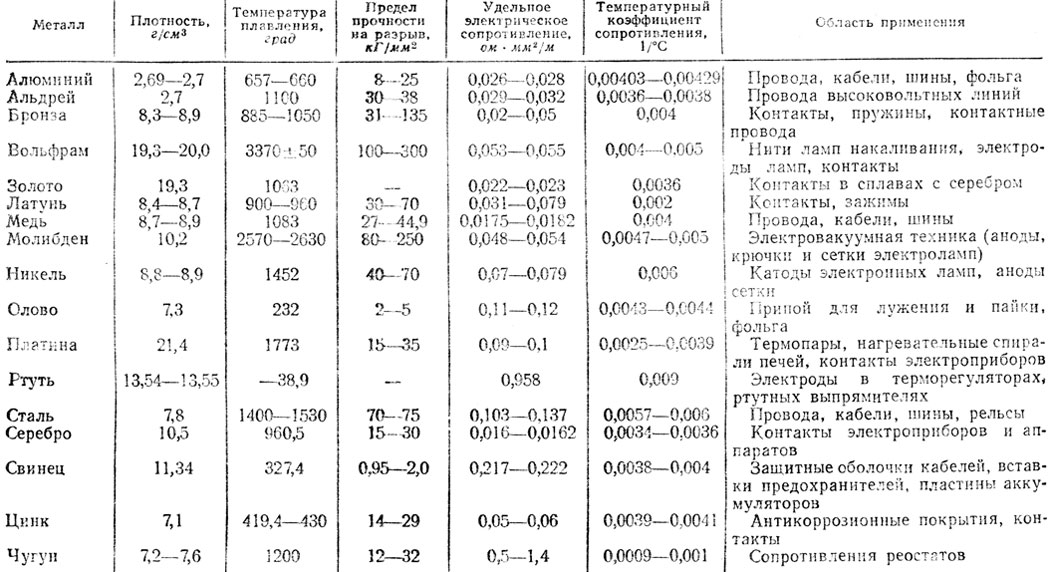 Таблица удельной величины для различных проводников
Таблица удельной величины для различных проводников
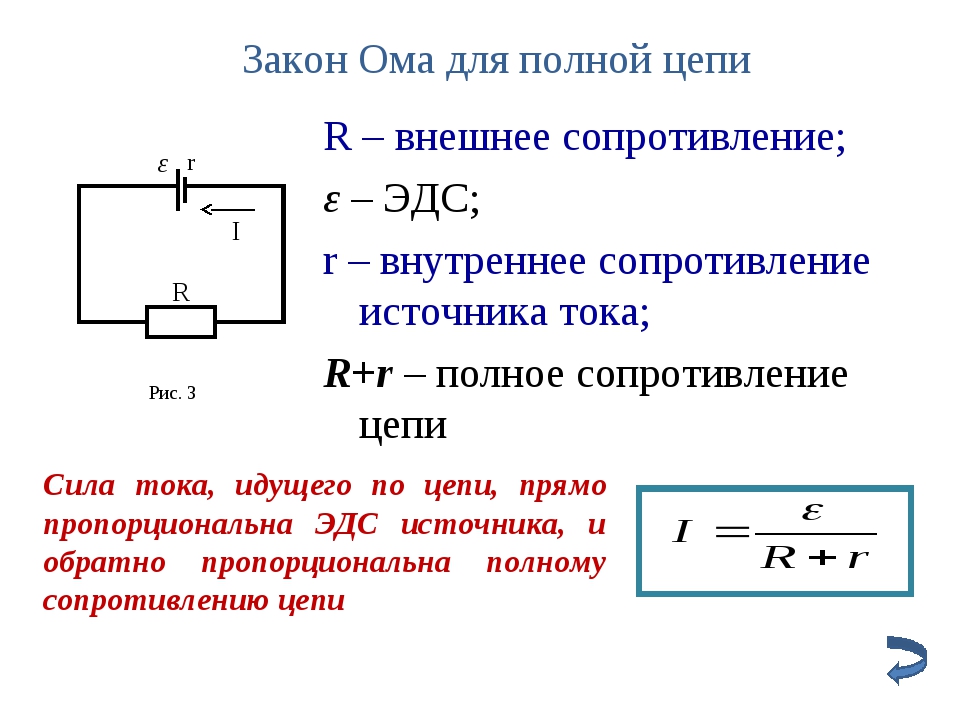
Реактивное внутреннее сопротивление
Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.
Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.
На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.
Расчёт
До изучения технологий вычислений необходимо уточнить основные определения:
- ветвями называют цепи с одним током;
- узлы – это места их соединения;
- контуры – замкнутые пути прохождения токов по нескольким ветвям.
Следует отдельно отметить два постулата. Они получили специфическое название «правила (законы) Кирхгофа» по фамилии ученого, сформулировавшего базовые принципы.
Первый закон (I1 + I2 + … + In = 0) определяет равным нулю суммарное значение всех токов, которые входят и выходят из одной точки в месте соединения нескольких ветвей.
Надо подчеркнуть! Данное выражение является точным для любых комбинаций компонентов, включенных в соответствующие цепи (резисторов, источников тока и других). Для удобства и наглядности расчетов учитывают входящие в узел токи с положительным знаком, выходящие – с отрицательным.
Второе правило упомянуто в качестве промежуточного вывода при рассмотрении последовательно включенных резисторов (Uип = U1 + U2 + U3). В классической формулировке закон утверждает равенство суммарных ЭДС источников питания и потенциалов на пассивных элементах, объединенных в одном расчетном контуре.
Последовательное соединение резисторов
С учетом сделанных определений можно составить формулу для любого количества резисторов, установленных в единой цепи без разветвлений:
Rобщ = R1 + R2 + … + Rn.
Вне зависимости от иных внешних компонентов, токи на входе и выходе в соответствии с первым правилом Кирхгофа будут одинаковыми.
Пример:
- Uип = 6,5B;
- R1= 8 Ом;
- R2 = 12 Ом;
- R3 = 4 Ом;
- Rобщ = 8 + 12 + 4 = 24 Ом;
- I = 6,5/24 = 0,27 А;
- U1 = I * R1 = 0,27 * 8 = 2,16 В;
- U2 = 0,27 * 12 = 3,24 В;
- U3 = 0,27 * 4 = 1,08 В.
Чтобы проверить последовательное соединение, формула на основе второго правила Кирхгофа пригодится:
Uип = 2,16 + 3,24 +1,08 ≈ 6,5 В.
Расчет подтвердил отсутствие ошибок.
Параллельное соединение резисторов
В этом варианте токи разделяются на входе и соединяются на выходе (первый закон Кирхгофа). Направление движения устанавливают от положительной клеммы с отрицательной подключенного источника питания. В соответствии с рассмотренными выше правилами при равенстве напряжений на отдельных резисторах токи в соответствующих цепях будут разными.
Для примера можно использовать предыдущие исходные данные:
общее сопротивление при параллельном соединении формула для трех компонентов:
Rобщ = R1*R2*R3/(R1*R2 + R2*R3 + R1*R3
- вставив номиналы, делают расчет Rобщ = 8 * 12 * 4 / (8*12 + 12*4 +8*4) = 2,182 Ом;
- I = 6,5/ 2,182 ≈ 2,98 А;
- I1 = 6,5/ 8 = 0,8125 А;
- I2 = 6,5/12 ≈ 0,5417 А;
- I3 = 6,5/4 = 1,625.
Как и в предыдущем случае, расчет проверяют. Если применяют параллельное сопротивление, формула вычислений должна подтвердить равенство токов:
I = 0,8125 + 0,5417 + 1,6225 = 2,9767 ≈ 2,98 А.
Соблюдено суммарное равенство входных и выходных значений для отдельного узла, поэтому ошибки отсутствуют.
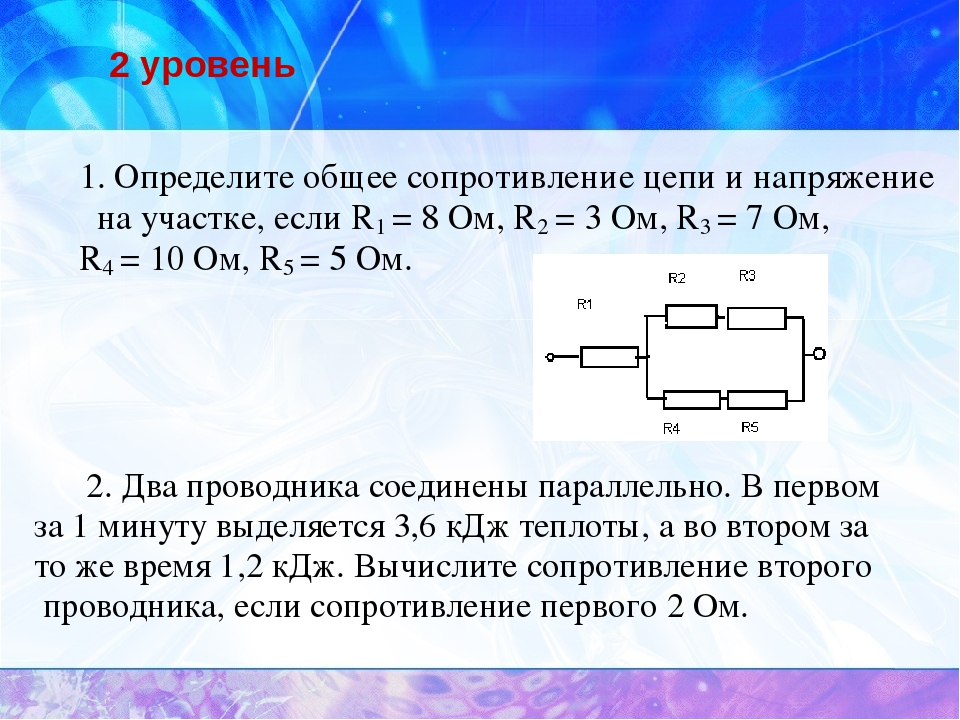
Смешанное соединение резисторов
Если в схеме присутствует комбинация последовательных и параллельных соединений, выполняют последовательно упрощение, пользуясь представленными методиками расчетов.
 Последовательное преобразование схемы для упрощения вычислений
Последовательное преобразование схемы для упрощения вычислений
На следующем рисунке показана последовательность преобразований:
- по значениям установленных R3 и R4 определяют общее значение для участка цепи Rэ;
- далее вычисляют сопротивление последовательных компонентов Rэ и R6;
- на следующем этапе делают расчет для группы R2, Rэк и R5;
- завершающее действие – суммирование R1, Rэ и R7 (рис. ниже).
Итоговый результат (Rэк) будет определять общее (эквивалентное) электрическое сопротивление группы резисторов. При необходимости вычисляют значения токов и напряжений в отдельных ветвях.
Последовательное соединение сопротивлений
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.
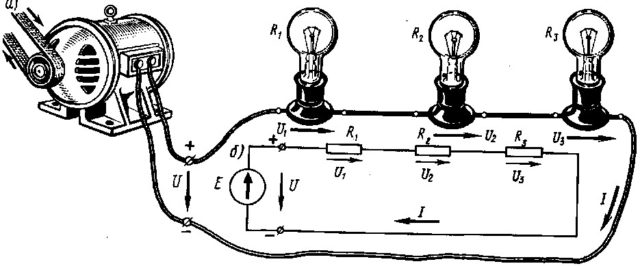
Лампы накаливания соединенные последовательно, можно рассматривать как сопротивления
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2).
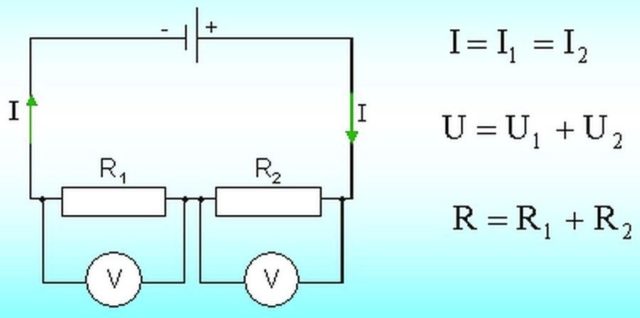
Последовательно соединенные сопротивления. I1 — ток протекающий через резистор R1, I2 — ток протекающий через резистор R2
Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают.
Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В.

Так понятнее, что такое последовательное соединение
Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом. Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В.
От чего зависит сопротивление резистора
Температура и последовательность включения – два главных фактора, которые определяют сопротивление в цепи. Но помимо этих показателей есть и допуски. Как же измерять? В большинстве электрических или электронных цепей большой 20% -ный допуск на один и тот же резистор, как правило, не является проблемой, но если для высокоточных цепей, таких как фильтры, генераторы или усилители и т. д., требуются резисторы с малым допуском, то необходимо использовать резистор с правильным допуском. Так как резистор с допуском 20% обычно не может использоваться для замены типа допуска 2% или даже 1%.
Цветовой код пяти- и шестиполосного резистора чаще всего ассоциируется с высокопрецизионными типами пленок 1% и 2%, в то время как универсальные садовые разновидности 5% и 10% общего назначения обычно используют четырехполосный цветовой код резистора. Резисторы имеют различные допуски, но наиболее распространенными являются E12 и E24 .
Е12 серия поставляется в двенадцати значений сопротивления за десятилетие (А десятилетие , представляющее кратные 10, то есть 10, 100, 1000 и т.д.), в то время как Е24 серия приходит в двадцать четыре значений за десятилетие и E96 серии девяносто шесть значений за десятилетие. Серия E192 с очень высокой точностью теперь доступна с допусками до ± 0,1%, что дает массивные 192 значения отдельных резисторов за десятилетие.

Как зависит от температуры
Чем выше температура, тем выше сопротивление. Это связано с быстрой скоростью движения атомов внутри твердого тела. Обратное явление – сверхпроводимость при низких температурах. Опять же, не забываем про погрешность.
От других параметров
Если резистор подключен в сложную цепь с множеством преобразующих, защитных, трансформирующих, компрессирующих устройств, то он будет иметь другое, отличное от стандартного, сопротивление, так как часть напряжения все равно будет проходить через него в нескомпрессированном виде, что не позволит ему отработать как следует. Чтобы более точно узнать удельный ток и сопротивление, показатель, полученный в расчетах, нужно уменьшить или увеличить на заданную величину.
Метод — эквивалентное сопротивление
Метод эквивалентных сопротивлений применяется для расчета таких электрических цепей, в которых имеются пассивные элементы, включенные между собой последовательно, параллельно или по смешанной схеме.
Для каких сетей применяется метод эквивалентного сопротивления.
Например, для использования метода эквивалентных сопротивлений при большом числе эквивалентируемых линий их можно находить не по результатам расчетов потокораспределения в каждой конкретной сети, как это было показано в параграфе 9.7, а на основании регрессионных зависимостей.
Как определяются потери электроэнергии методом эквивалентного сопротивления.
|
К расчету электрической цепи методом наложения. |
Каждая частная схема рассчитывается отдельно, например, методом эквивалентных сопротивлений. Ток в данной ветви исходной схемы определяется алгебраической суммой частных токов этой ветви.
Ориентировочные величины Н наносим на схему над стояками. С помощью метода эквивалентных сопротивлений этот расчет может быть произведен несколько быстрее.
|
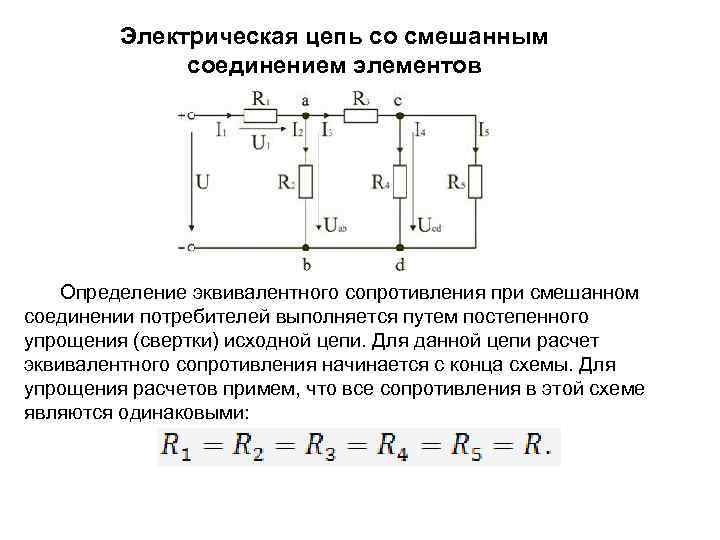
Схема цепи со смешанным соединением сопротивлений. |
Пусть все сопротивления и напряжение на входе этой схемы заданы и требуется определить токи ее отдельных участков. Для расчета воспользуемся методом эквивалентных сопротивлений, по которому отдельные участки схемы упрощают и постепенным преобразованием их приводят схему к одному общему ( входному) сопротивлению. Для упрощения схемы отдельные группы последовательно или параллельно соединенных сопротивлений заменяют одним эквивалентным сопротивлением.
|
К методу эквивалентных сопротивлений. |
В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает расчет.
|
Схема линий тока при фильтрации газа к горизонтальному. |
Во втором способе истинная область фильтрации заменяется областью с гиперболическим характером изменения толщины пласта h ( R) в интервале Rc h ( R) RK. В работе для определения производительности горизонтальных скважин использован метод эквивалентных сопротивлений, который заменяет пространственную задачу фильтрации газа плоской. Ниже приведены конечные расчетные формулы, полученные с использованием метода эквивалентных сопротивлений для определения производительности горизонтальных газовых скважин.
|
Замена сопро — 2 — 3. Замена.| Разветвленная цепь с одним источником питания. |
На схеме рис. 2 — 1 приведен пример электрической цепи с одним источником питания и смешанным соединением сопротивлений. Распределение токов в ней при заданных напряжении и сопротивлениях участков можно определить методом эквивалентных сопротивлений. Для этого отдельные участки схемы упрощают и постепенным преобразованием их приводят к одному общему эквивалентному сопротивлению.
Практические задания:
-
Ход работы:
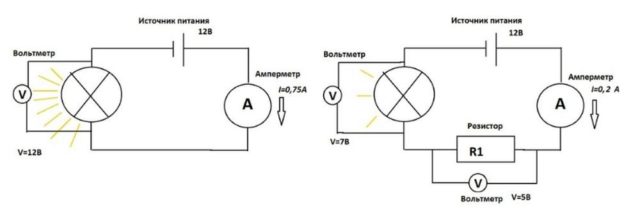
1) Подключите лабораторный блок питания (далее, БП) к вольтметру (рисунок ниже). С помошью ручки регулятора (располагается на блоке питания) изменяйте напряжение на вольтметре пока он не покажет значение 9 Вольт. Поскольку, внутреннее сопротивление блока питаия мало (
2) Собрите электрическую цепь, состоящую из источника ЭДС (лабораторный блок питания), переменного резистра, постоянного резистра R, вольтметра(мультиметр в режиме измерения напряжения) и ключа К (разомкнутого) по следующей схеме:
3) С помошью переменного резистра установите внутреннее сопротивление источника ЭДС. Для этого возьмите еще один мультиметр и установите его в режим измерения сопротивления. Подсоедините его щупы к переменному резистру r. Теперь, установите сопротивление резистра:
А) 0 Ом — внутреннее сопротивление равно сопротивлению БП
Б) 30 Ом — внутреннее сопротивление примерно равно сопротивлению батарейки типа «крона».
В) 100 Ом — внутреннее сопротивление достаточно плохого источника. После установки сопротивления для каждого из вариантов А), Б), В), необходимо отключать мультиметр, используемый для измерения сопротивления.
4)Далее, необходимо:
Замкнуть ключ K. С помощью вольтметра измерить падение напряжения на резистре R для случаев A, Б и B. Проанализировать полученные результаты, на основании замеров сделать вывод о внутреннем сопротивлении источников питания.
5)Сфотографируйте и разместите этапы сборки.
6)Заполните таблицу падений напряжения для случаев А,Б,В.
-
Ход работы:
1)Соберите электрическую цепь, состоящую из источника ЭДС, двух последовательно соединенных резисторов R1, R2 и вольтметра (мультиметр в ежиме измерения напряжения) согласно схеме:
В качестве источника ЭДС возьмите лабораторный БП (установите на 15 вольт).
Используйте резистры R1 и R2 сопротивлениями:
А) 1КОм, 1КОм.
Б) 1КОм, 2КОм.
В) 1КОм, 5КОм.
Г) 1КОм, 10КОм.
2)Для всех вариантов А-Г с помощью мультиметра измерьте падение напряжения на участке С-B. Проанализируйте полученные результаты. В каких отношениях резистры делят напряжение?
Лабораторные работы Технологии+Бизнес
Основные понятия
Электрический ток течёт, когда замкнутый контур позволяет электронам перемещаться от высокого потенциала к более низкому в цепи. Иначе говоря, ток требует источника электронов, обладающего энергией для приведения их в движение, а также точки их возвращения отрицательных зарядов, для которой характерен их дефицит. Как физическое явление ток в цепи характеризуется тремя фундаментальными величинами:
- напряжение;
- сила тока;
- сопротивление проводника, по которому движутся электроны.
Сила и напряжение
Сила тока (I, измеряется в Амперах) есть объём электронов (заряд), перемещающихся через место в цепи за единицу времени. Иными словами, измерение I — это определение количества электронов, находящихся в движении
Важно понимать, что термин относится только к движению: статические заряды, например, на клеммах неподсоединённой батареи, не имеют измеряемого значения I. Ток, который протекает в одном направлении, называется постоянным (DC), а периодически изменяющий направление — переменным (AC)
Напряжение можно проиллюстрировать таким явлением, как давление, или как разность потенциальной энергии предметов под воздействием гравитации. Для того чтобы создать этот дисбаланс, нужно затратить предварительно энергию, которая и будет реализована в движении при соответствующих обстоятельствах. Например, в падении груза с высоты реализуется работа по его подъёму, в гальванических батареях разность потенциалов на клеммах образуется за счёт преобразования химической энергии, в генераторах — в результате воздействия электромагнитного поля.
Сопротивление проводников
Независимо от того, насколько хорош обычный проводник, он никогда не будет пропускать сквозь себя электроны без какого-либо сопротивления их движению. Можно рассматривать сопротивление как аналог механического трения, хотя это сравнение не будет совершенным. Когда ток протекает через проводник, некоторая разность потенциалов преобразуется в тепло, поэтому всегда будет падение напряжения на резисторе. Электрические обогреватели, фены и другие подобные устройства предназначены исключительно для рассеивания электрической энергии в виде тепла.
Упрощённо сопротивление (обозначается как R) является мерой того, насколько поток электронов тормозится в цепи. Оно измеряется в Омах. Проводимость резистора или другого элемента определяется двумя свойствами:
- геометрией;
- материалом.
Форма имеет важнейшее значение, это очевидно на гидравлической аналогии: протолкнуть воду через длинную и узкую трубу гораздо тяжелее, чем через короткую и широкую. Материалы играют определяющую роль. Например, электроны могут свободно перемещаться в медном проводе, но не способны протекать вообще через такие изоляторы, как каучук, независимо от их формы. Кроме геометрии и материала, существуют и другие факторы, влияющие на проводимость.
Параллельное соединение резисторов.
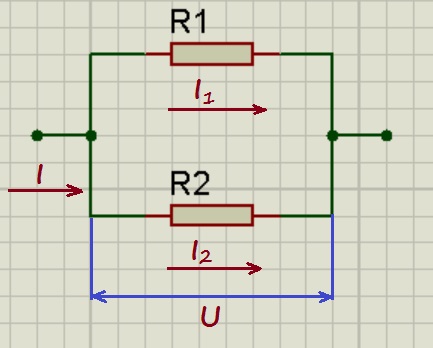
При параллельном соединении напряжения на проводниках равны:
U_1 = U_2 = U
А для токов справедливо следующее выражение:
I = I_1 + I_2
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
I_1 = \frac{U_1}{R_1} = \frac{U}{R_1}
I_2 = \frac{U_2}{R_2} = \frac{U}{R_2}
Подставим эти выражения в формулу общего тока:
I = \frac{U}{R_1} + \frac{U}{R_2} = U\medspace (\frac{1}{R1} + \frac{1}{R2})
А по закону Ома ток:
I = \frac{U}{R_0}
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2}
Данную формулу можно записать и несколько иначе:
R_0 = \frac{R_1R_2}{R_1 + R_2}
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
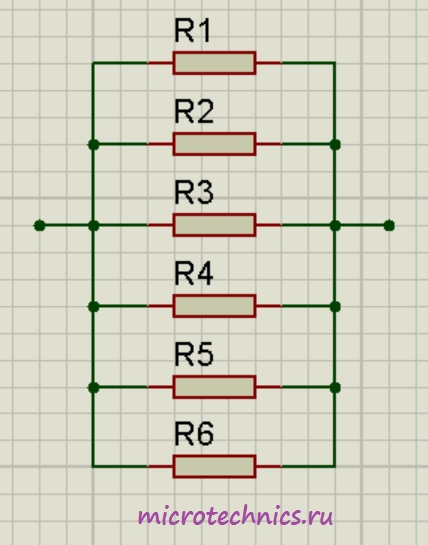
\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_5} + \frac{1}{R_6}
Как найти сопротивление резистора в цепи
Система цветового кода резистора хороша, но нам нужно понять, как ее применять, чтобы получить правильное значение резистора. «Левая» или наиболее значимая цветная полоса – это полоса, ближайшая к соединительному выводу, полосы с цветовой кодировкой читаются слева направо следующим образом:
Цифра, цифра, множитель = цвет, цвет х 10 цветов в омах (Ω)
Например, резистор имеет следующие схемы маркировки;
Желтый Фиолетовый Красный = 4 7 2 = 4 7 x 10 2 = 4700 Ом или 4 кОм Ом.
Типичные допуски на резисторы для пленочных резисторов варьируются от 1% до 10%, в то время как для углеродных резисторов допуски составляют до 20%. Резисторы с допусками ниже 2% называются прецизионными, а резисторы с более низким допуском более дорогими. Само напряжение играет малую роль.
Большинство пятиполосных резисторов являются прецизионными резисторами с допусками 1% или 2%, в то время как большинство четырехполосных резисторов имеют допуски 5%, 10% и 20%. Цветовой код, используемый для обозначения номинального допуска резистора, имеет вид:
Коричневый = 1%, красный = 2%, золото = 5%, серебро = 10%
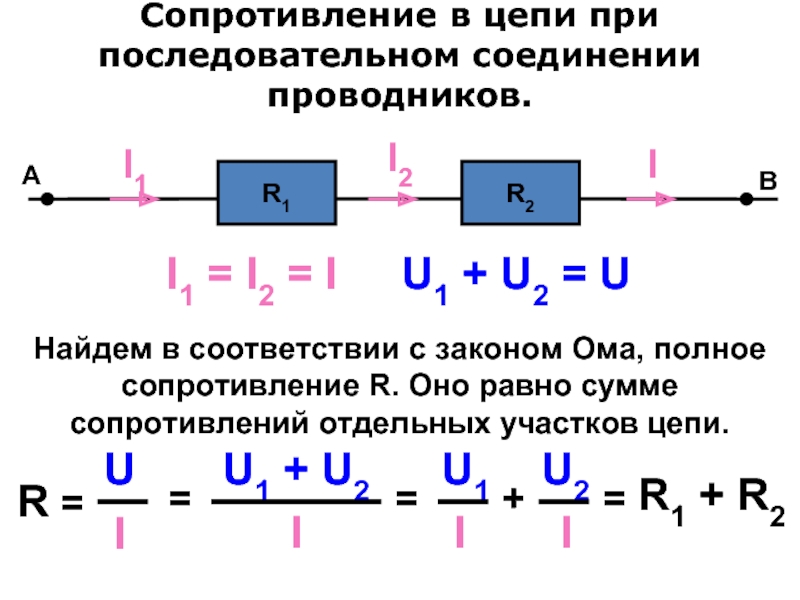
При последовательном соединении
Общее сопротивление цепи при последовательном соединении в электрической цепи равно сумме сопротивлений отдельных проводников (или отдельных участков цепи): R = R 1 + R 2.
Могут ли быть погрешности и какие
Если резистор не имеет четвертой полосы допусков, тогда допуск по умолчанию будет обозначаться 20% . Остальной ток будет рассеиваться.
Полученная мнемоника сопоставляет первую букву каждого слова каждому цвету, который составляет цветовой код резисторов в порядке возрастания величины, и есть много разных мнемонических фраз, которые можно использовать. Однако эти высказывания часто бывают очень грубыми, но тем не менее эффективными для запоминания цветов резисторов, но все же помогают определить сопротивление.
Таблица погрешнойстей для более точного определения сопротивления
| Коды допусков для резисторов (±) |
| B = 0,1% |
| С = 0,25% |
| D = 0,5% |
| F = 1% |
| G = 2% |
| J = 5% |
| К = 10% |
| М = 20% |
Кроме того, при чтении этих письменных кодов соблюдайте осторожность, чтобы не перепутать букву сопротивления k для килограммов с буквой допуска K для допуска 10% или буквой сопротивления M для мегаом с буквой допуска M для допуска 20%
Последовательное подключение
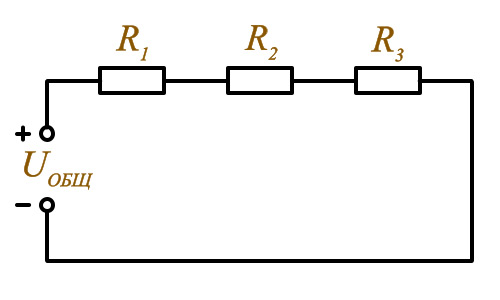 Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше. Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.
Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше. Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.
Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях — складываем, в параллельных — это обратно пропорциональная величина.
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2). Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых. Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
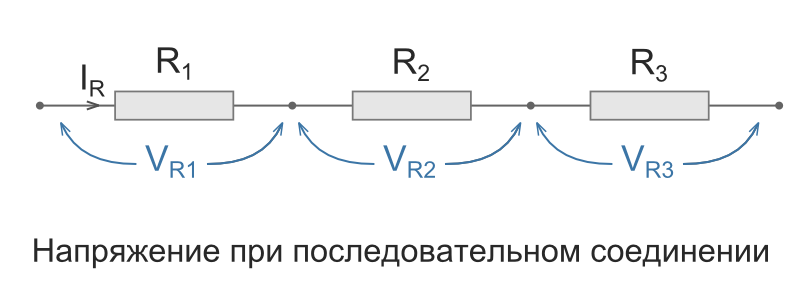 Последовательное подключение.
Последовательное подключение.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
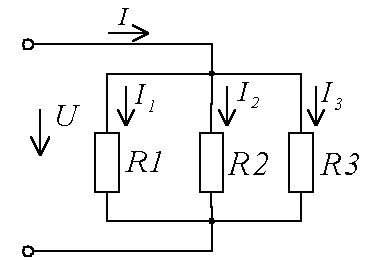 Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.
Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Заказать решение ТОЭ
- Метрология Электрические измерения
- Пигарев А.Ю. РГЗ по электротехнике и электронике в Multisim
-
Теория линейных электрических цепей ТЛЭЦ
-
—
Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: задание на контрольные работы № 1 и 2 с методическими указаниями для студентов IV курса специальности Автоматика, телемеханика и связь на железнодорожном транспорте-
—
Контрольная работа №1 -
—
Контрольная работа №2
-
—
-
—
-
Электротехника и основы электроники
-
—
Электротехника и основы электроники: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений / Соколов Б.П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил-
—
Контрольная работа № 1 Электрические цепи -
—
Контрольная работа № 2 Трансформаторы и электрические машины -
—
Контрольная работа № 3 Основы электроники
-
—
-
—
-
Теоретические основы электротехники ТОЭ
-
—
Артеменко Ю.П., Сапожникова Н.М. Теоретические основы электротехники: Пособие по выполнению курсовой работы МГТУ ГА 2009 -
—
Переходные процессы Переходные процессы в электрических цепях -
—
Теоретические основы электротехники Методические указания и контрольные задания для студентов технических специальностей вузов-
—
Задание 1 Линейные электрические цепи постоянного и синусоидального тока-
—
Задача 1.1 Линейные электрические цепи постоянного тока -
—
Задача 1.2 Линейные электрические цепи синусоидального тока
-
—
-
—
Задание 2 Четырехполюсники, трехфазные цепи, периодические несинусоидальные токи, электрические фильтры, цепи с управляемыми источниками
-
—
-
—
Теоретические основы электротехники сб. заданий Р.Я. Сулейманов Т.А. Никитина Екатеринбург УрГУПС 2010 -
—
Трехфазные цепи. Расчет трехфазных цепей -
—
УГТУ-УПИ Решение ТОЭ Билеты по ТОЭ -
—
Электромагнитное поле Электростатическое поле Электростатическое поле постоянного тока в проводящей среде Магнитное поле постоянного тока
-
—