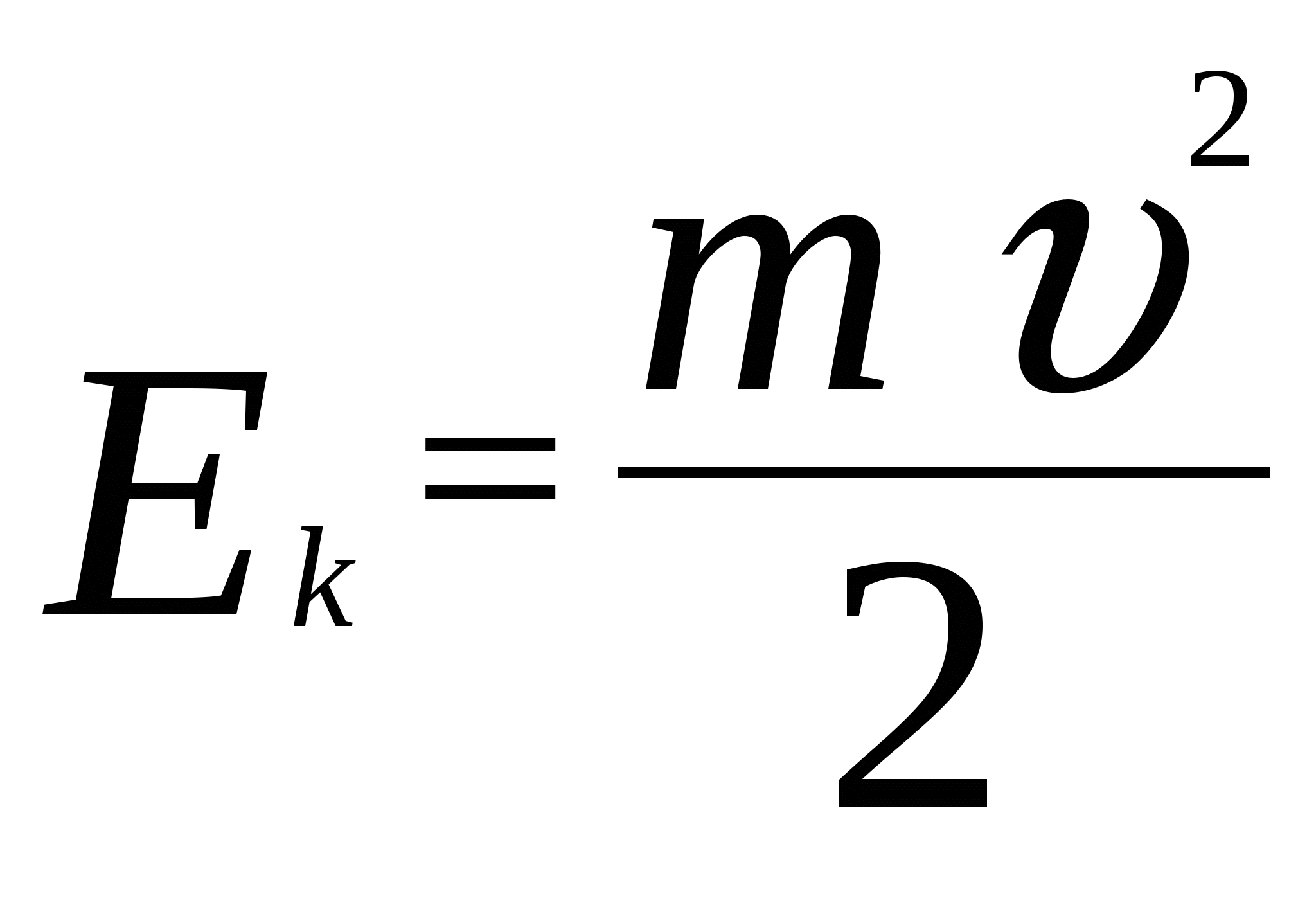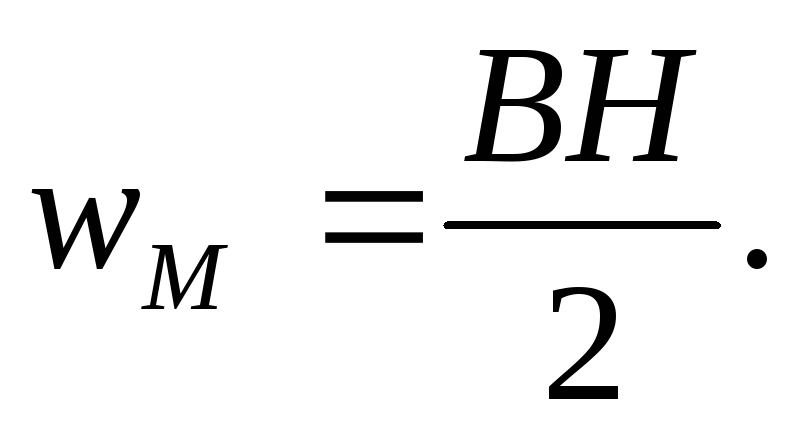- Объемная плотность магнитной энергии
- Мощность электрического тока в цепи
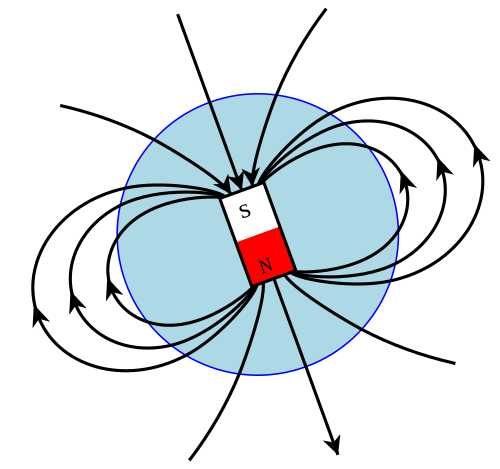
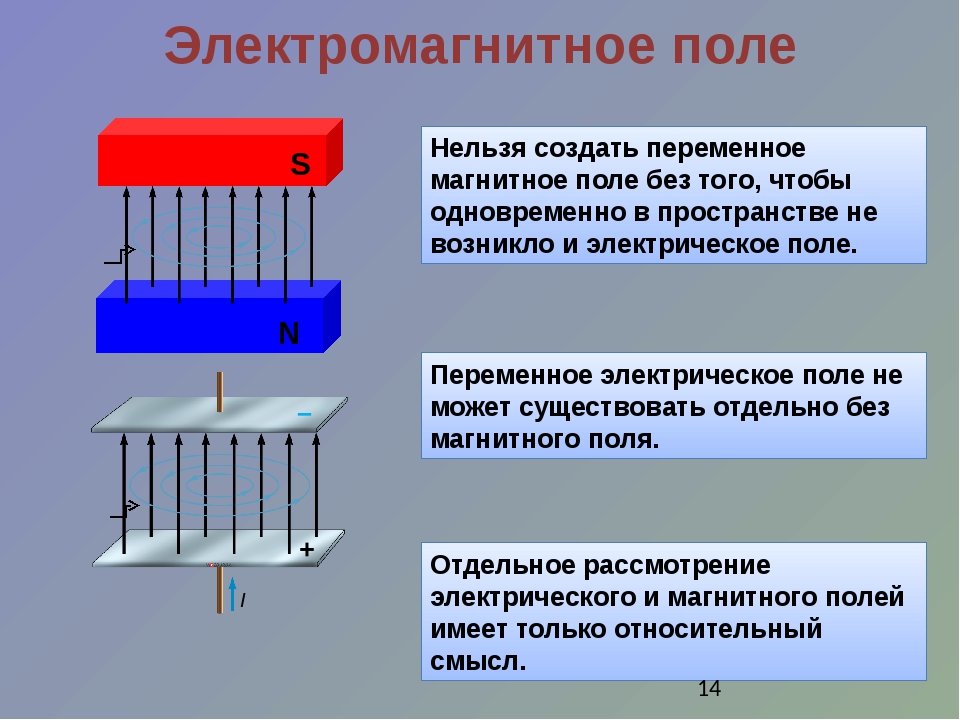
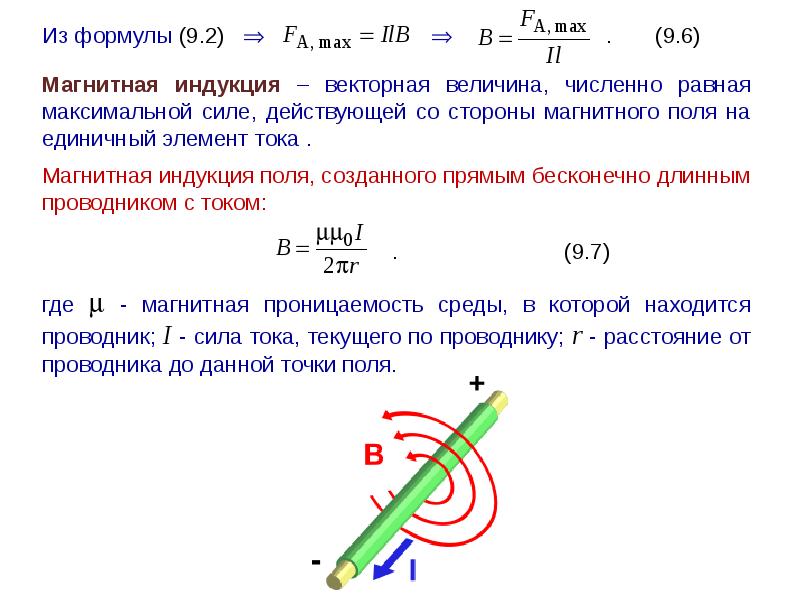
- Наличие магнитного поля вокруг проводника или катушки с током
- Работа электрического поля по перемещению заряда
- «Действие магнитного поля на проводник с током»
- Электрический двигатель
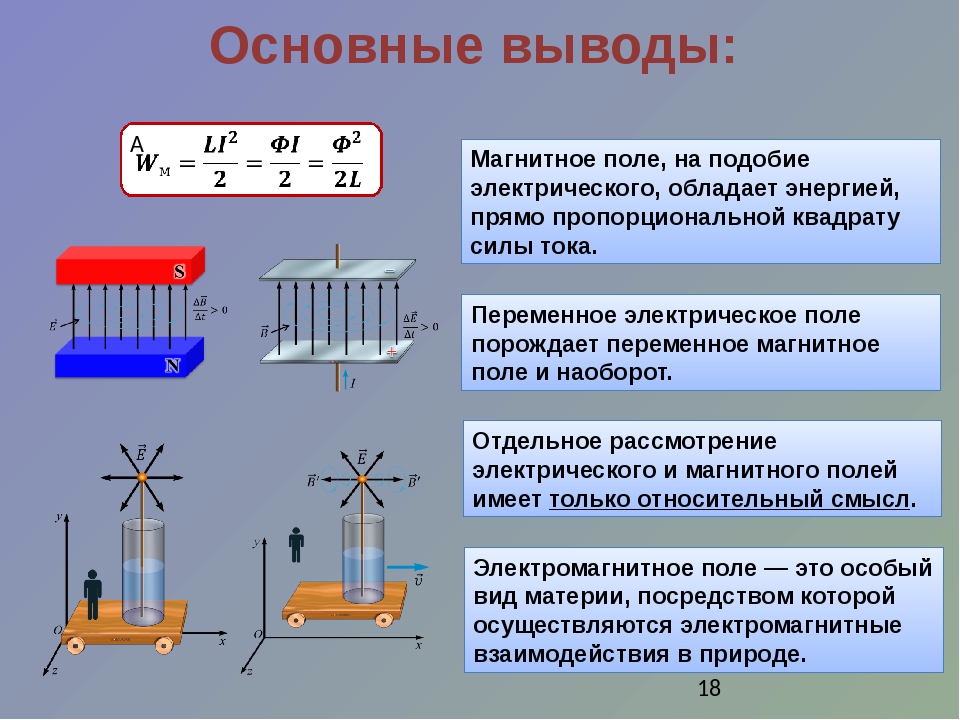
- Энергия электрического и магнитного полей
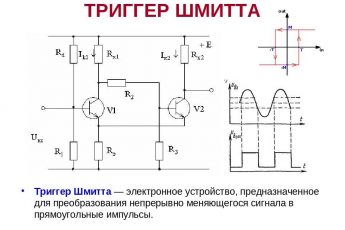
- Формула индуктивного сопротивления катушки
- Плотность энергии различных систем
- Измерение плотности энергии магнитных полей
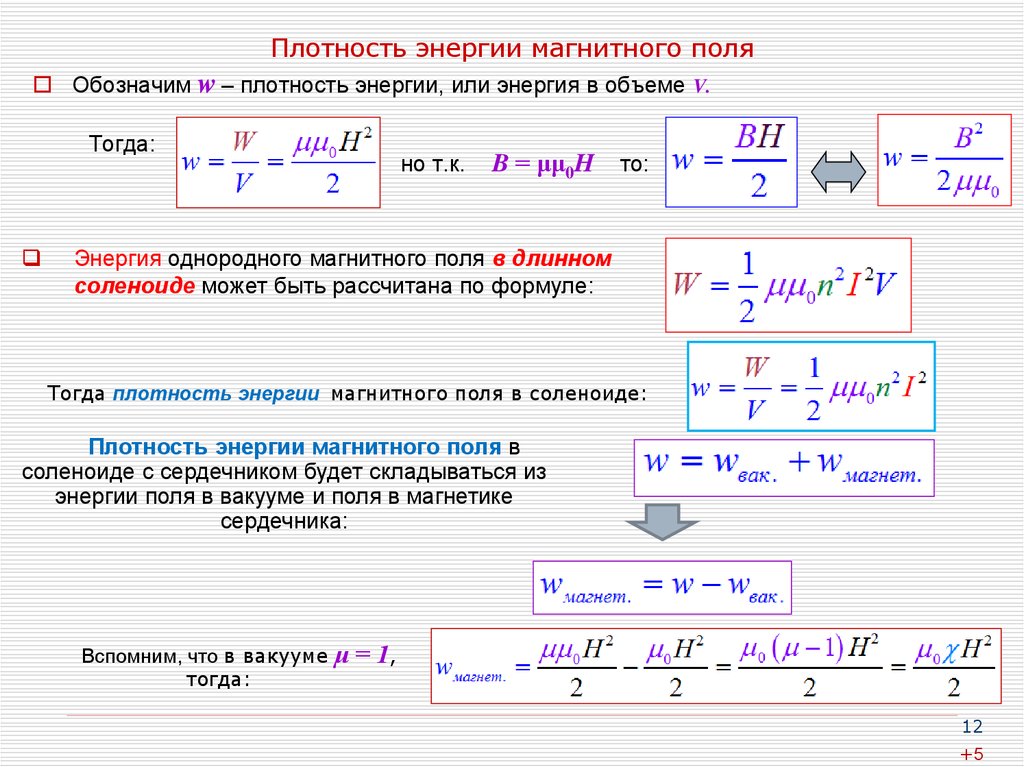
Объемная плотность магнитной энергии
Формула нахождения объемной плотности энергии имеет такой вид:
ω=W/V.
Под ω здесь подразумевается собственно искомая плотность, под W – энергия имеющегося поля, под V – объем пространства, в котором поле проявляет активность. Если выразить значение W через магнитную проницаемость µ и индукцию В и подставить в формулу, она приобретет следующий вид:
ω=В2/2* µ0* µ (здесь µ0 – это магнитная постоянная).
Преобразование с использованием вектора индукции применяется, чтобы исключить привязку активного магнитного поля к особенностям дросселя. Формула для вычисления индукционной характеристики выглядит так:
B= µ0* µ*I*n.
I здесь – токовая сила в катушечной цепочке, через n выражается такая величина, как плотность обмотки. Она равна частному количества витков в соленоидной обмотке и длины фрагмента, на котором размещены витки. Тогда формула для W
W= В2*V/2* µ0* µ.
Подставив выражение в основную формулу плотности, можно привести его к ранее обозначенному виду.
Мощность электрического тока в цепи
Мощность P{\displaystyle P} электрического тока для участка цепи определяется обычным образом, как производная от работы A{\displaystyle A} по времени, то есть выражением:
- P(t)=dAdt=U(t)⋅I(t),{\displaystyle P(t)={\frac {dA}{dt}}=U(t)\cdot I(t),}
Это наиболее общее выражение для мощности в электрической цепи.
С учётом закона Ома
- U=I⋅R{\displaystyle U=I\cdot R}
электрическую мощность, выделяемую на сопротивлении R{\displaystyle R}, можно выразить как через ток
- P=I(t)2⋅R,{\displaystyle P=I(t)^{2}\cdot R,}
так и через напряжение:
- P=U(t)2R.{\displaystyle P={{U(t)^{2}} \over R}.}
Соответственно, работа (выделившаяся теплота) является интегралом мощности по времени:
- A=∫P(t)dt=∫I(t)2⋅Rdt=∫U(t)2Rdt.{\displaystyle A=\int P(t)\,dt=\int I(t)^{2}\cdot R\,dt=\int {{U(t)^{2}} \over R}\,dt.}
Наличие магнитного поля вокруг проводника или катушки с током
При подключении соленоида (катушки) в электрическую цепь вокруг нее формируется поле. Характеристики поля зависят от ряда параметров: от средовых особенностей окружения, токовой силы (она измеряется в амперах) и материала, из которого изготовлен проводник или обмотка катушки. В полевом пространстве могут образовываться электромагнитные волны. Так как на полевой энергетический потенциал, прежде всего, оказывает влияние сила текущего в системе электротока, можно сделать вывод, что работа тока по генерированию магнитного пространства будет эквивалентной энергии последнего. Если в систему подключена катушка с магнитным сердечником, то на энергетическую плотность будет влиять полевая энергия в вакууме и в материале, из которого сделан сердечниковый элемент.
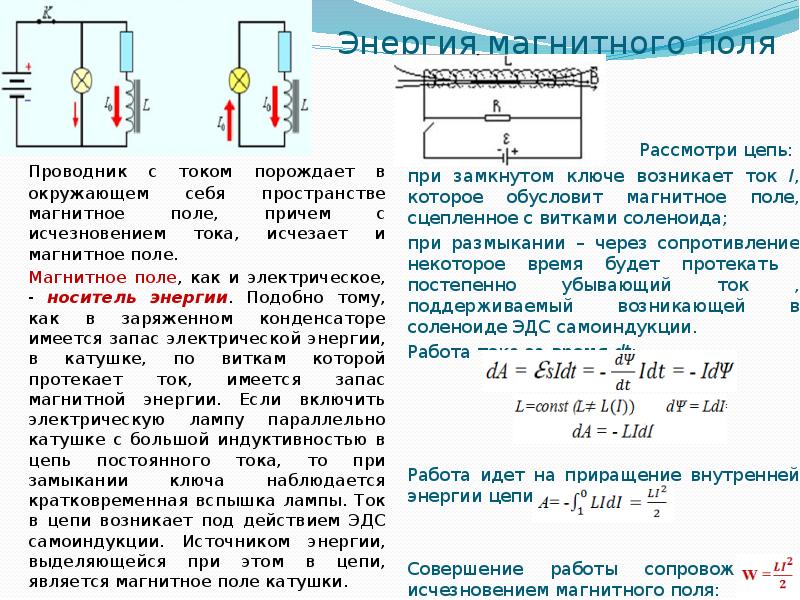
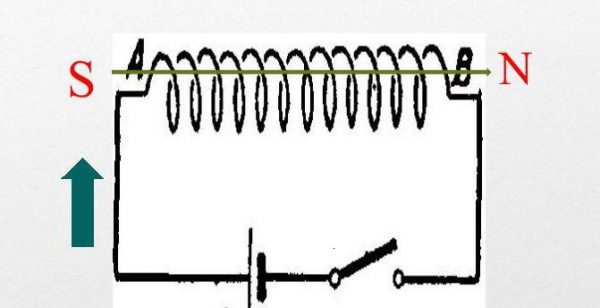 Подключение индуктивной катушки к источнику тока
Подключение индуктивной катушки к источнику тока
Для изучения динамики явления можно рассмотреть электроцепь, включающую в себя дроссель, лампу, замыкающий ключ и источник постоянного электротока. Когда ключик замыкается, токовый путь будет идти от «положительного» зажима источника через лампу и индуктивную катушку. Поначалу лампа накаливания загорится ярче, что связано со значительной величиной сопротивления дроссели. По мере того, как сопротивление будет падать, а проходящий через обмотку ток увеличиваться, интенсивность горения лампочки будет понижаться. Связано это с тем, что первое время подаваемый на дроссель ток имеет значение, пропорциональное току высокой частоты.
Чтобы практически построить цепь, подходящую для расчета, нужно, чтобы энергетический ресурс источника питания затрачивался на генерирование магнитного поля. Поэтому параметрами внутреннего сопротивления дроссели и питательного источника допустимо пренебрегать.
Важно! Согласно второму закону Кирхгофа, сумма подсоединенных к электрической цепи напряжений равняется сумме снижений напряжения для всех компонентов цепочки. Второй закон Кирхгофа
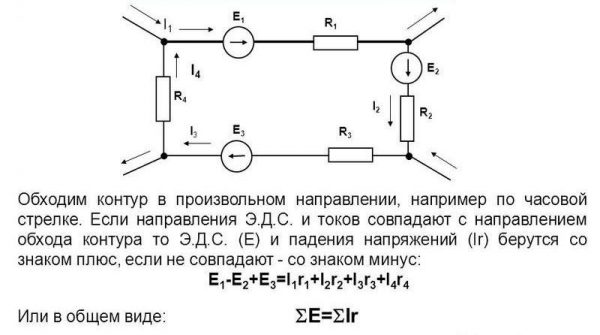 Второй закон Кирхгофа
Второй закон Кирхгофа
Работа электрического поля по перемещению заряда
Понятие работы A{\displaystyle A} электрического поля E{\displaystyle E} по перемещению заряда Q{\displaystyle Q} вводится в полном соответствии с определением механической работы:
- A=∫F(x)dx=∫Q⋅E(x)dx=Q⋅U,{\displaystyle A=\int F(x)\,dx=\int Q\cdot E(x)\,dx=Q\cdot U,}
где U=∫Edx{\displaystyle U=\int E\,dx} — разность потенциалов (также употребляется термин напряжение).
Во многих задачах рассматривается непрерывный перенос заряда в течение некоторого времени между точками с заданной разностью потенциалов U(t){\displaystyle U(t)}, в таком случае формулу для работы следует переписать следующим образом:
- A=∫U(t)dQ=∫U(t)I(t)dt,{\displaystyle A=\int U(t)\,dQ=\int U(t)I(t)\,dt,}
где I(t)=dQdt{\displaystyle I(t)={dQ \over dt}} — сила тока.
«Действие магнитного поля на проводник с током»
Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.
Сила Ампера зависит от длины проводника с током, силы тока в проводнике, модуля магнитной индукции и расположения проводника относительно линий магнитной индукции: FA = BIlsinа.
Для определения направления силы Ампера применяют правило левой руки. Если левую руку расположить в магнитном поле так, чтобы силовые линии входили в ладонь, а четыре пальца были направлены по току, то отогнутый большой палец укажет направление силы, действующей на проводник.
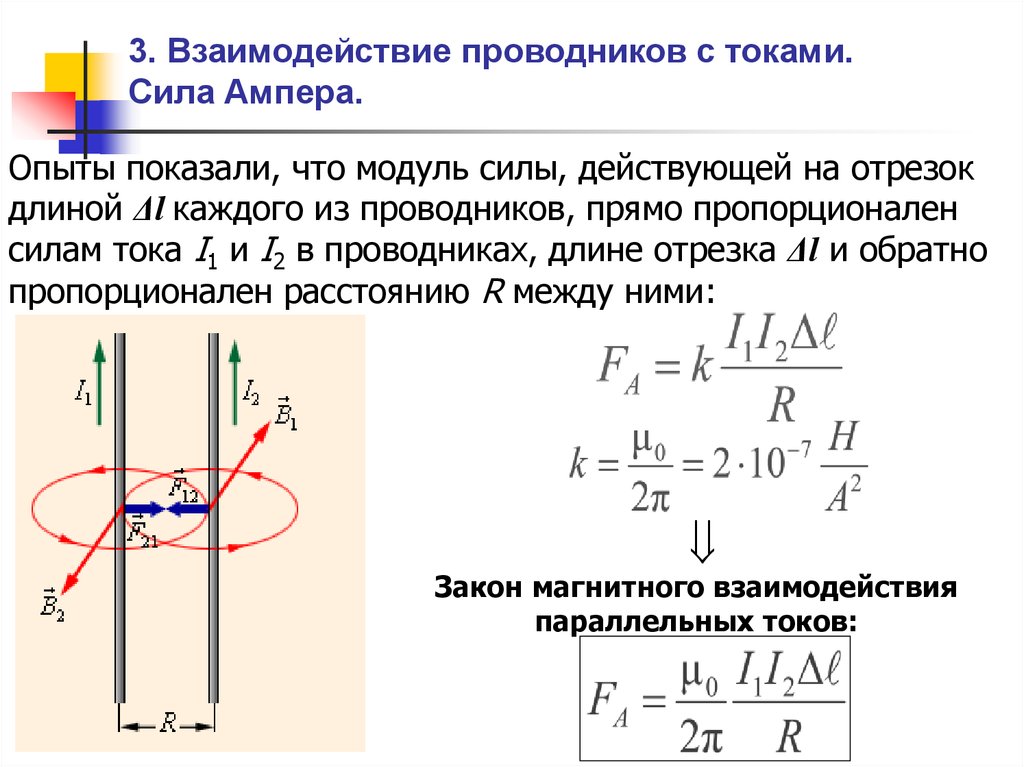
Магнитное взаимодействие можно наблюдать между двумя параллельными токами (опыт Ампера): два параллельных проводника с током отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают.
Экспериментальное исследование показывает, что сила Ампера прямо пропорциональна длине проводника l и силе тока I в проводнике. Коэффициентом пропорциональности в этом равенстве является модуль вектора магнитной индукции В. Соответственно, F = BIl. В таком виде зависимость силы, действующей на проводник с током в магнитном поле, записывается в том случае, если линии магнитной индукции перпендикулярны проводнику с током. Из приведённой формулы понятно, что магнитная индукция является силовой характеристикой магнитного поля.
Единица магнитной индукции = 1Н / 1А • 1м = 1 Тл. За единицу магнитной индукции принимают магнитную индукцию такого поля, в котором на проводник длиной 1 м действует сила 1Н при силе тока в проводнике 1 А.
Магнитное поле действует также на движущиеся заряженные частицы. При этом сила (сила Лоренца) зависит от модуля магнитной индукции, заряда частицы, а также от модуля и направления её скорости.
Электрический двигатель
Движение проводника с током в магнитном поле лежит в основе работы электрического двигателя. Если поместить прямоугольную рамку в магнитное поле и пропустить по ней электрический ток, то рамка повернётся, потому, что на стороны рамки действует сила Ампера. При этом сила, действующая на сторону рамки ab, противоположна силе, действующей на сторону cd.
Для того чтобы рамка не остановилась в тот момент, когда её плоскость перпендикулярна линиям магнитной индукции, и продолжала вращаться, изменяют направление тока в проводнике. Для этого к концам рамки припаяны полукольца, по которым скользят контакты, соединённые с источником тока. При повороте рамки на 180° меняются контактные пластины, которых касаются полукольца и, соответственно, направление тока в рамке.
В электрическом двигателе энергия электрического и магнитного полей превращается в механическую энергию.
Действие магнитного поля на проводник с током
Конспект урока по физике в 8 классе «Действие магнитного поля на проводник с током».
Следующая тема: «Электромагнитная индукция. Опыты Фарадея».
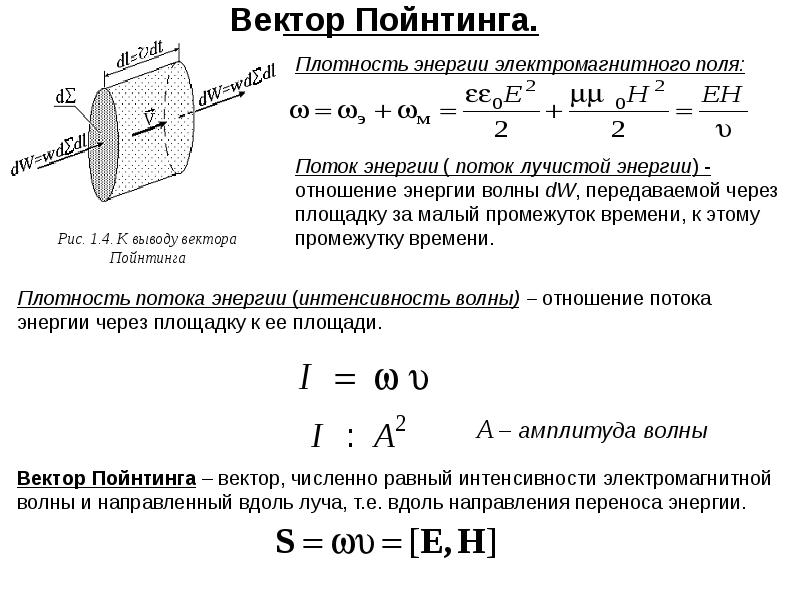
Энергия электрического и магнитного полей
Для электрического и магнитного полей их энергия пропорциональна квадрату напряжённости поля. Строго говоря, термин «энергия электромагнитного поля» является не вполне корректным. Вместо него в физике обычно используют понятие плотности энергии электромагнитного поля (в определённой точке пространства). Общая энергия поля равняется интегралу плотности энергии по всему пространству.
Плотность энергии электромагнитного поля является суммой плотностей энергий электрического и магнитного полей.
В системе СИ:
- u=E⋅D2+B⋅H2.{\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} }{2}}+{\frac {\mathbf {B} \cdot \mathbf {H} }{2}}.}
В вакууме (а также в веществе при рассмотрении микрополей):
- u=εE22+B22μ=εE2+c2B22=E2c2+B22μ,{\displaystyle u={\varepsilon _{0}E^{2} \over 2}+{B^{2} \over {2\mu _{0}}}=\varepsilon _{0}{\frac {E^{2}+c^{2}B^{2}}{2}}={\frac {E^{2}/c^{2}+B^{2}}{2\mu _{0}}},}
где E — напряжённость электрического поля, B — магнитная индукция, D — электрическая индукция, H — напряжённость магнитного поля, с — скорость света, ε{\displaystyle \varepsilon _{0}} — электрическая постоянная и μ{\displaystyle \mu _{0}} — магнитная постоянная. Иногда для констант ε{\displaystyle \varepsilon _{0}} и μ{\displaystyle \mu _{0}} — используют термины диэлектрическая проницаемость и магнитная проницаемость вакуума, — которые являются крайне неудачными, и сейчас почти не употребляются.
В системе СГС:
- u=E⋅D+B⋅H8π.{\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} +\mathbf {B} \cdot \mathbf {H} }{8\pi }}.}
Формула индуктивного сопротивления катушки
Формула магнитного потока
Вычислить величину сопротивления дросселя XL можно, воспользовавшись следующей формулой:
XL=2πfL.
Здесь буква L обозначает параметр индуктивности дроссели, а f – токовую частоту. Исходя из этого выражения, поначалу попадающий на обмотку ток будет пропорциональным электротоку большой чистоты. В это время дроссель проявляет поведение, аналогичное ситуации цепного разрыва, с сильным повышением индуктивного сопротивления. С течением времени последнее падает до нулевого значения.
Вмонтированная в лампу нитка отличается высоким показателем сопротивления, тогда как активный показатель обмотки, напротив, стремится к нулю. Из-за этого возникает ситуация, когда почти весь цепной ток проходит через дроссель. Когда цепь размыкают при помощи ключа, лампа не затухает постепенно. Напротив, она сначала резко начинает гореть интенсивно, потом – медленно угасать. Чтобы лампа горела, требуется энергетический ресурс. Он поступает из магнитного поля, генерируемого индуктивной катушкой. Таким образом, дроссель проявляет себя источником самоиндукции.
В рассмотренном примере катушка с обмотками, подключенная в цепь, выступает как источник магнитного поля. Поскольку в такой ситуации это поле не является однородным, для выполнения расчетов необходимо использование показателя, характеризующего концентрацию и распределение энергии в поле. Можно заключить, что смысл введения параметра плотности поля состоит именно в этом.
Плотность энергии различных систем
В таблице приведена плотность энергии замкнутых систем, включая дополнительные внешние компоненты, такие как окислители или источники тепла, но исключая энергию покоя системы в конечном состоянии. 1 МДж ≈ 278 Вт·ч.
| Название | Плотность энергии на единицу массы (МДж/кг) | Плотность энергии на единицу массы (Вт⋅ч/кг) | Плотность энергии на единицу объёма (МДж/л) | Практическая эффективность использования % |
|---|---|---|---|---|
| Аннигиляция материя + антиматерия | до 89 875 517 873,681 764 (точно) ≈ 9⋅1010 | 24 965 421 631 578,26(7) ≈ 25⋅1012 | Зависит от вступающих в реакцию частиц, электроны и позитроны аннигилируют полностью, при аннигиляции барионов часть энергии в конечном счёте уносят нейтрино | |
| Слияние ядер водорода | 645 000 000 | 179 310 000 000 | ~1–10⋅1012(в ядре Солнца) | |
| Реакция дейтерий-тритий | 337 000 000 | 93 686 000 000 | ||
| Уран-235, используемый в ядерном оружии | 88 250 000 | 24 533 500 000 | 1 681 000 000 | |
| Природный уран (99,3 % U-238, 0,7 % U-235) в реакторе на быстрых нейтронах | 86 000 000 | 23 908 000 000 | ||
| Тепловая энергия от α-распада плутония-238 | 2 200 000 | 611 600 000 | 43 648 000 | |
| Кинетическая энергия спутника Земли на низкой орбите | 33 | 9 167 | ||
| Дизельное топливо в мощной дизельной электростанции (без учёта массы генератора) | 20,1 | 5 583 | 47 % | |
| Бензин (без учёта массы генератора) | 8,1—10,5 | 2250—2917 | 19—24 % | |
| Супермаховик | 1,8 | 500 | 98% | |
| Генератор на водородном топливном элементе, без учёта массы конструкции | 12 | 3000 | ||
| Серебряно-цинковый аккумулятор | 0,47 | 130,6 | 1,8 | |
| Литий-ионный аккумулятор | 0,46—0,72 | 128—200 | 2 | |
| Ni-MH-аккумулятор формата AA ёмкостью 2000 мА·ч | 0,33 | 92 | 1,24 | |
| Тяговый свинцово-кислотный аккумулятор | 0,17 | 47 | ||
| Пусковой свинцово-кислотный аккумулятор | 0,1368 | 38 | 0,337 | |
| 0,1 | ||||
| Ионистор | 0,03 | 6,17 | 0,032 (MAXWELL K2) | |
| Керамический конденсатор | 0,003 | |||
| Электролитический конденсатор | 0,000 639 | 0,1775 | 0,00083 | |
| Плёночный конденсатор | 0,000 180 | 0,05 | 0,0025 (maxwell CM-3) | |
| Гравитационный аккумулятор (груз 1 кг на высоте 1 м) | 0,000 009 8 | 0,0027 | 0,0001 для свинца | |
| Взведенная | 0,0003 | 0,083 | 0,0006 |
Измерение плотности энергии магнитных полей
Свободная энергия эфира: генераторы свободной энергии
Данная величина показывает энергию, содержащуюся в единице объема окружающей среды, подпадающей под влияние поля. Обозначается она греческой буквой ω. Для вычисления применяется формула:
ω=W/V, в данном случае W – это полевая энергия в объеме пространства V.
Единица измерения плотности поля в международной системе СИ тоже выглядит как частное единиц, в которых измеряются эти величины: джоулей и кубических метров (Дж/м3). Показатель для аккумуляторов (ионных, свинцово-кислотных и других) указывают в прилагающейся документации.
Для соленоида, подсоединенного в электрическую цепь, оба составляющих этого частного можно выразить через следующие единицы:
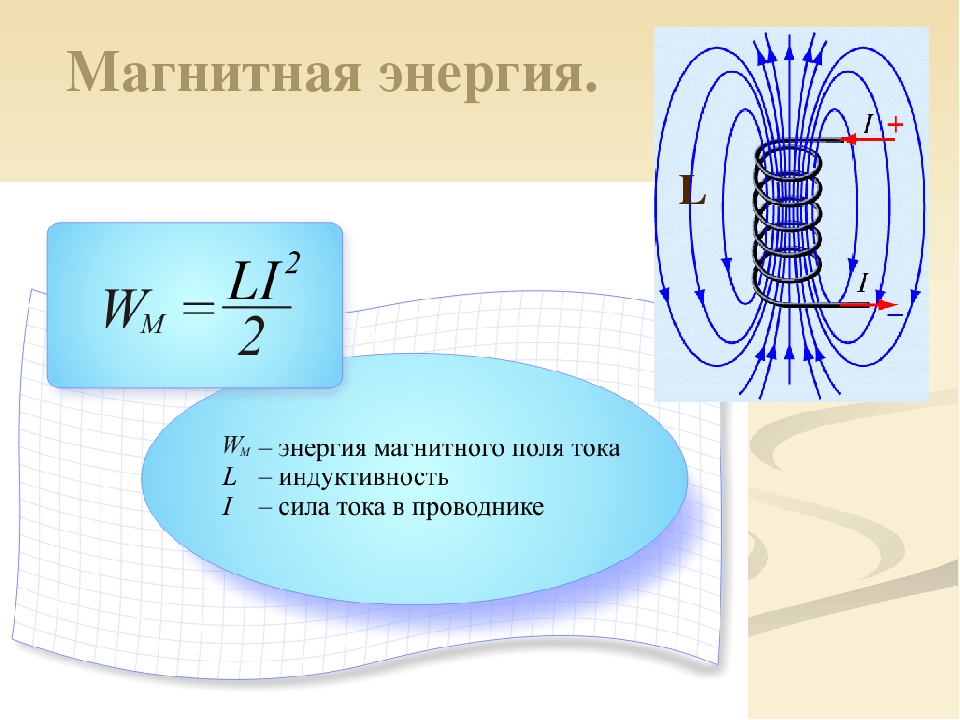
- Значение энергетического ресурса поля будет равным уполовиненному произведению индуктивности соленоида на квадрат токовой силы в его обмотке:
W=L*I2/2.
- В качестве «пространства» рассматривается сама катушка, тогда V=S*l, где S – площадь сечения катушечного элемента в поперечнике, а l – его длина.
Тогда конечная формула принимает следующий облик:
ω=L*I2/2*S*l.