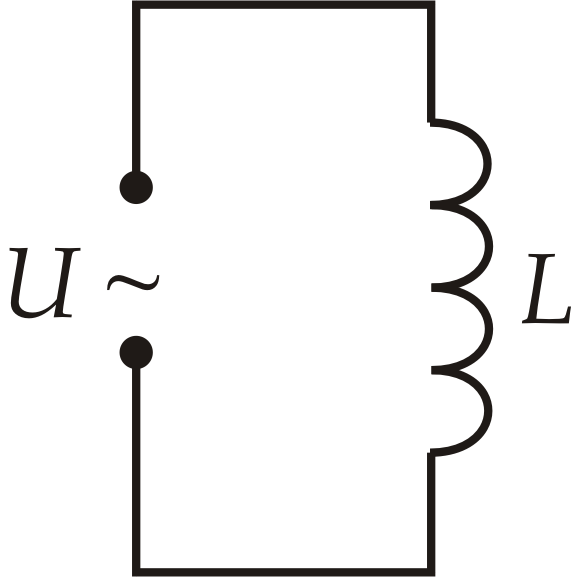Индуктивность проводника

Индуктивность одновиткового контура и индуктивность катушки

Величина магнитного потока, пронизывающего одновитковый контур, связана с величиной тока следующим образом:

Φ=LI{\displaystyle \displaystyle \Phi =LI}

где L{\displaystyle L} — индуктивность витка. В случае катушки, состоящей из N витков предыдущее выражение модифицируется к виду:

Ψ=LI{\displaystyle \displaystyle \Psi =LI}

где Ψ=∑i=1NΦi{\displaystyle \Psi =\sum \limits _{i=1}^{N}{\Phi _{i}}} — сумма магнитных потоков через все витки (это так называемый полный поток, называемый в электротехнике потокосцеплением, именно он фигурирует в качестве магнитного потока вообще в случае для катушки в общем определении индуктивности и в теоретическом рассмотрении выше; однако для упрощения и удобства для многовитковых катушек в электротехнике пользуются отдельным понятием и отдельным обозначением), а L{\displaystyle L} — уже индуктивность многовитковой катушки. Ψ{\displaystyle \Psi } называют потокосцеплением или полным магнитным потоком. Коэффициент пропорциональности L{\displaystyle L} иначе называется коэффициентом самоиндукции контура или просто индуктивностью.

Если поток, пронизывающий каждый из витков одинаков (что довольно часто можно считать верным для катушки в более или менее хорошем приближении), то Ψ=NΦ{\displaystyle \Psi =N\Phi }. Соответственно, LN=L1N2{\displaystyle L_{N}=L_{1}N^{2}} (суммарный магнитный поток через каждый виток увеличивается в N раз — поскольку его создают теперь N единичных витков, и потокосцепление ещё в N раз, так как это поток через N единичных витков). Но в реальных катушках магнитные поля в центре и на краях отличаются, поэтому используются более сложные формулы.

Индуктивность

По своей сути индуктивность является электрической инерцией и ее основное свойство состоит в том, чтобы оказывать сопротивление всякому изменению протекающего тока. Если через катушку пропускать определенный ток, то ее индуктивность будет противодействовать как уменьшению, так и увеличению протекающего тока.

В отличие от конденсатора, который пропускает переменный и не пропускает постоянный ток, катушка индуктивности свободно пропускает постоянный ток и оказывает сопротивление переменному току, потому что он изменяется быстрее, чем может изменяться магнитное поле.

И чем больше индуктивность катушки и чем выше частота тока, тем оказываемое сопротивление сильнее. Это свойство катушки применяют, например, в приемной аппаратуре, когда требуется в электрической цепи преградить путь переменному току.

Индуктивность измеряется в генри (Гн), миллигенри (1мГн = 10ˉ3 Гн), микрогенри (1мкГн = 10ˉ6 Гн), наногенри (1нГн = 10ˉ9 Гн) и обозначается латинской буквой L.

Соединение катушек при наличии взаимного влияния их магнитных полей.

Если катушки, включенные в цепь последовательно, распо­ложены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше фор­мула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:

1. Магнитные потоки обеих катушек имеют одинаковые на­правления
2. Магнитные потоки обеих катушек направлены навстречу друг другу

Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений то­ков в них.

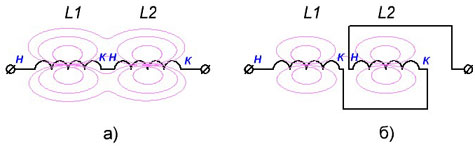
Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.

Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответство­вать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.

Разберем первый случай, когда магнитные потоки направ­лены в одну сторону. Очевидно, при этих условиях витки каж­дой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в дру­гой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых состав­лена цепь.

Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.

Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по фор­муле:

В первом случае ставится знак + (плюс), а во втором слу­чае знак — (минус).

Величина М, называемая коэффициентом взаим­ной индукции, представляет собой добавочную индук­тивность, обусловленную частью магнитного потока, общей для обеих катушек.

На явлении взаимоиндукции основано устройство варио­метров. Вариометр состоит из двух катушек, общая индуктив­ность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передат­чиков.

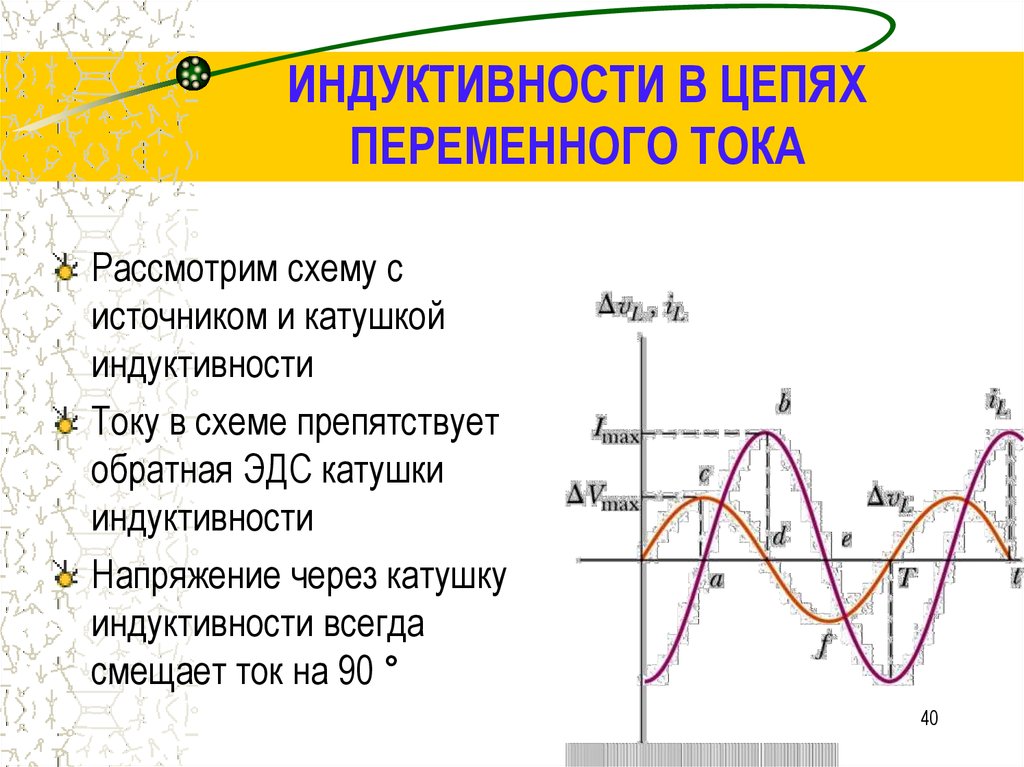
График зависимости тока и ЭДС самоиндукции от времени

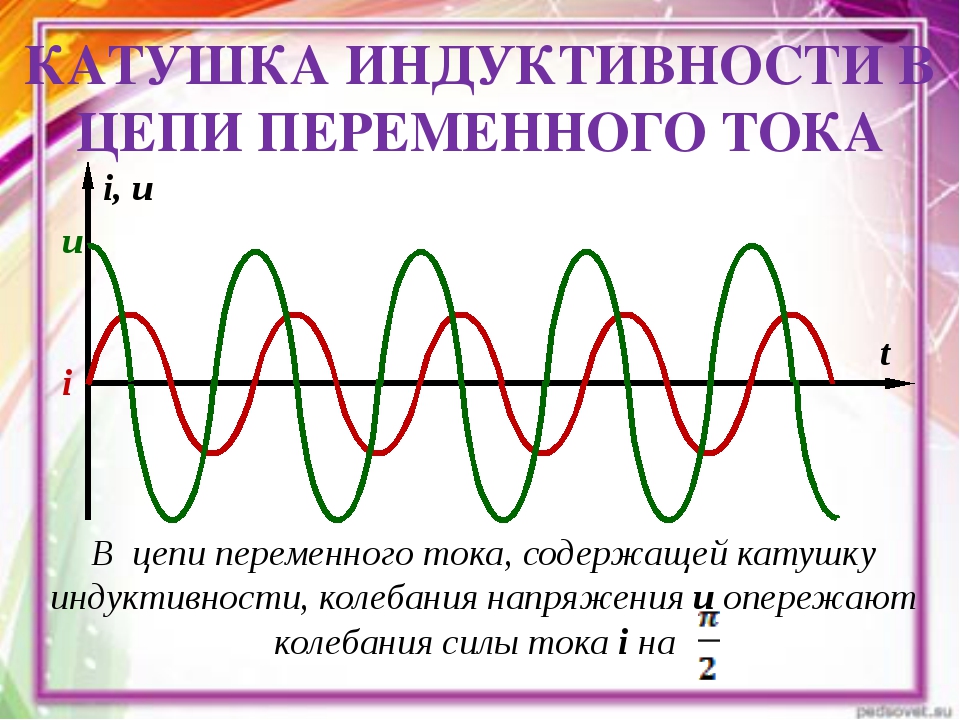
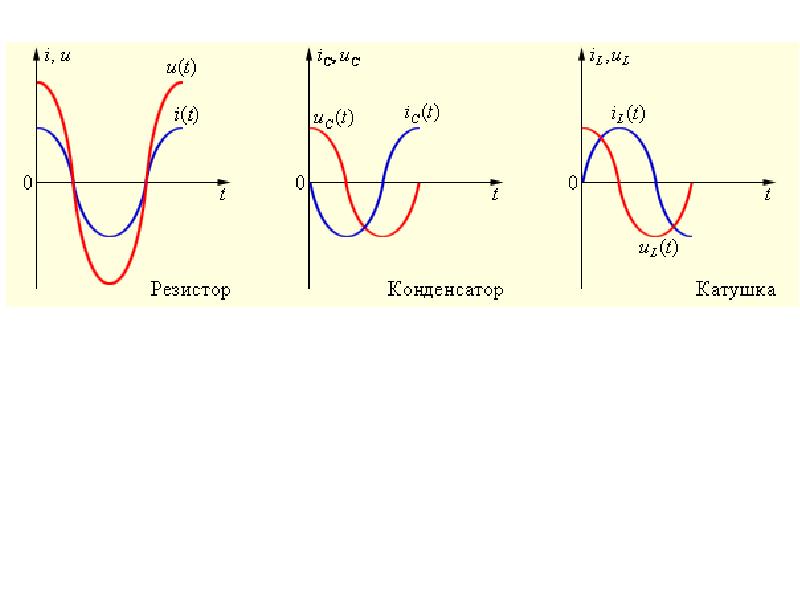
Графически характер изменения тока в цепи и ЭДС самоиндукции с течением времени выглядит так:

Зависимость тока и ЭДС самоиндукции в катушке в цепи переменного тока

Из графика видно, что ЭДС самоиндукции тем больше, чем выше скорость изменения силы тока. В начале периода (участок вблизи т.1 на графике) сила тока возрастает быстро, потому и ЭДС самоиндукции здесь максимальна. К концу первой четверти периода (т. 2) скорость изменения снижается почти до нуля (синусоида принимает горизонтальное положение), после чего сила тока все стремительнее уменьшается (участок между т. 2 и т. 3).

Соответственно, ЭДС самоиндукции снижается в т. 2 до нуля, а затем снова возрастает, но при этом меняет знак на противоположный: теперь она противодействует падению силы тока, то есть ток и ЭДС по знаку совпадают. В следующем полупериоде картина повторяется.

Что такое индуктивность

Что такое индуктивность — это физическая величина, которая рассказывает нам о магнитных свойствах электрической цепи. Индуктивность измеряют в Гн (Генри).

Если вы вообще не понимаете о чём речь, то советую ознакомиться сначала с вот с этой статьей.

В электрических схемах например, нам встречаются какие-то непонятные катушки, дроссели и многие даже не знают их функциональную роль. В этой статье я постараюсь доступным языком рассказать, что такое индуктивность и как это явление применить на своей любимой работе.

Давайте посмотрим на рисунок

Давайте начнём движение проводника в магнитном поле таким образом, чтобы он пересек силовые линии постоянного магнита. Если это условие выполняется, то тогда в нашем проводнике появляется электродвижущая сила (ЭДС).  Или наоборот проводник остаётся на месте, а магнит передвигают таким образом, чтобы силовые линии магнита пересекали проводник. Сейчас был пример электромагнитной индукции. Значение индуцированной электродвижущей силы в проводнике прямо пропорциональна магнитной индукции поля, скорости перемещения и длине проводника

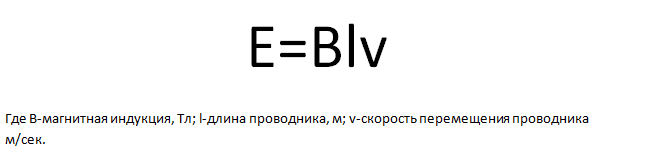
Направление возникшей электродвижущей силы в проводнике
определяют через правило правой руки.

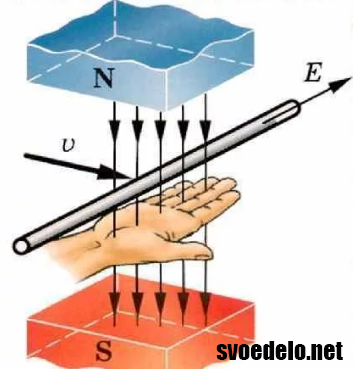
Правая рука находится в таком положении чтобы силовые линии
магнита заходили в ладонь. Следовательно, большой палец показывает нам направление
перемещения проводника, а остальные пальцы покажут нам направление возникшей
электродвижущей силы.

Для усиления электродвижущей силы индукции применяют электрические
катушки

А если подать напряжение на катушку, то по её виткам потечёт ток, который создаёт своё магнитное поле.

Устройство и принцип работы катушки индуктивности.

Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку То есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:

Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название Индуктивность – это способность преобразовывать энергию электрического поля в энергию магнитного поля. Это свойство катушки связано с тем, что при протекании по проводнику тока вокруг него возникает магнитное поле:

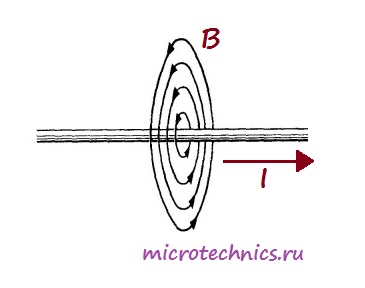
А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:

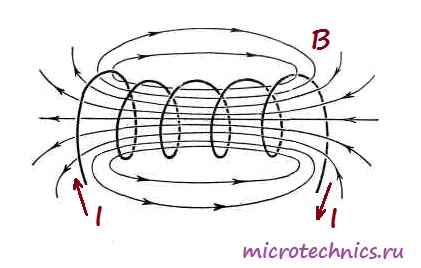
В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри – это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину индуктивности катушки можно рассчитать по следующей формуле:

L = \frac{\mu_0\thinspace \mu S N^2}{l}

Давайте разберемся, что за величину входят в это выражение:

• \mu_0 – магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению: \mu_0 = 4 \pi \cdot 10^{-7}\medspace\frac{Гн}{м}
• \mu – магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз
• S – площадь поперечного сечения катушки
• N – количество витков
• l – длина катушки

Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.

С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный!

Индуктивность в электрических цепях

В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.

В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:

Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:

где ω является угловой частотой резонансной частоты F:

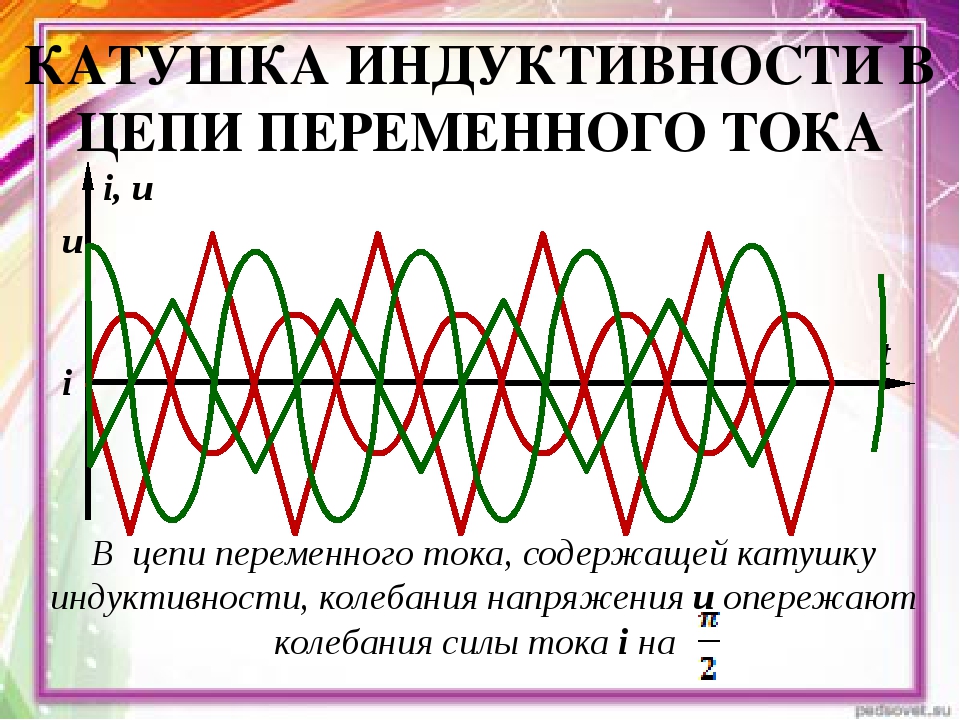
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.

 Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.

Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:

Методы расчёта индуктивностей

Индуктивностью (обозначается L) или коэффициентом самоиндукции называется коэффициент пропорциональности между потокосцеплением (обозначается Ψ­_L) и электрическим током, который возбуждает данное потокосцепление.

В простых случаях индуктивность можно рассчитать, применяя формулы для вычисления магнитной индукции B (закон Био-Савара-Лапласа), магнитного потока Φ и потокосцепления Ψ­_L

где S – площадь поверхности ограниченная контуром, который создает магнитную индукцию;

n – количество контуров с током, которые пронизывает магнитный поток.

Однако это в идеальном случае, в реальности говоря о токе I, который протекает по проводнику, необходимо отметить, что его распределение по сечению проводника не всегда равномерно, вследствие возникновения скин-эффекта при переменном токе. В результате этого эффекта плотность электрического тока распределяется неравномерно, происходит её уменьшение от внешнего слоя проводника к его центру. Уменьшение плотности тока также происходит неравномерно и зависит от частоты переменного тока. Для оценки скин-эффекта ввели понятие толщины скин-слоя ∆, которая показывает, на каком расстоянии от поверхности проводника плотность тока падает в е = 2,718 раз. Толщину скин-слоя можно вычислить по выражению

где δ – глубина проникновения переменного тока или толщина скин-слоя;

μ – магнитная проницаемость вещества;

γ – удельная электрическая проводимость материала проводника;

ω – круговая частота переменного тока, ω = 2πf.

Поэтому непосредственный способ вычисления индуктивности практически не применяется.

На практике применяется выражения для индуктивности, выведенные с некоторыми допущениями, погрешности вычисления индуктивности по этим выражениями составляет порядка нескольких процентов.

Так как индуктивные элементы довольно разнообразны, их можно разделить на три группы:

индуктивные элементы без сердечников;

индуктивные элементы с замкнутыми сердечниками;

индуктивные элементы с сердечниками, имеющие воздушный зазор.

Самые простые по конструкции являются индуктивные элементы без сердечников, поэтому рассмотрим их в первую очередь. Простейшим из таких элементов является прямой провод.

ОБЩАЯ ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Свойства катушек индуктивности

Метод определения собственной ем­кости катушек

Катушка индуктивности
—
является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.

Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.

Индуктивность — проводник

Индуктивность проводников Ь зависит от их формы и размеров.
 

Индуктивность проводника в данной среде определяется исключительно его размерами и формой. Индуктивность прямолинейного провода невелика. Индуктивность того же провода в форме витка значительно больше. При одинаковых размерах катушек ( длин и диаметров) их индуктивность пропорциональна квадрату числа витков. Индуктивность катушки прямо пропорциональна магнитной проницаемости ia сердечника.
 

Индуктивность проводника зависит от его формы, размеров, а также от свойств окружающей среды. Если сила тока изменяется со временем, то изменяется и магнитный поток, сцепленный с контуром. Изменение магнитного потока, в свою очередь, вызывает появление в проводнике индукционного тока. Так как индукционный ток вызван изменением силы тока в самом проводнике, то данное явление возникновения индукционного тока называется самоиндукцией, а возникающая эдс — эдс самоиндукции. Самоиндукция является частным случаем явления электромагнитной индукции.
 

Индуктивность проводника в данной среде определяется исключительно его размерами и формой. Индуктивность прямолинейного провода невелика. Индуктивность того же провода в форме витка значительно больше. При одинаковых размерах катушек ( длин и диаметров) их индуктивность пропорциональна квадрату числа витков. Индуктивность катушки прямо пропорциональна магнитной проницаемости ia сердечника.
 

Индуктивность проводника численно равна магнитному потоку, создаваемому током в 1 ампер, протекающему по данному проводнику.
 

Индуктивность проводника характеризует его размеры и форму, а также магнитную проницаемость среды, окружающей проводник. Индуктивность проводника остается постоянной, если не изменяется его форма, размеры и магнитная проницаемость окружающей его среды.
 

Индуктивность проводников проявляется только при прохождении через них изменяющегося со временем тока. В этой работе индуктивность определяется методом мостика, питаемого переменным током.
 

Индуктивность проводника L называется еще коэффи циентом самоиндукции.
 

Индуктивность проводников I, зависит от их формы и размеров.
 

Индуктивность L проводника определяется его формой, размерами, взаимным расположением отдельных его частей, средой, в которой происходит замыкание магнитного потока.
 

Индуктивность проводников L зависит от их формы и размеров.
 

Эффект близости.

Индуктивность проводника конечного сечения складывается из внешней и н д у к-тивности.
 

Параметры проводника длиной 100 мм.

Если индуктивность проводника, соединяющего экран с шасси ( корпусом), велика, то экран может не уменьшить, а увеличить емкостную паразитную связь.
 

Маркировка

Для обозначения номинала катушки индуктивности используют буквенную или цветовую маркировку. Есть два вида буквенной маркировки.

1. Обозначение в микрогенри.

2. Обозначение набором букв и цифр. Буква r – используется вместо десятичной запятой, буква в конце обозначения обозначает допуск: D = ±0.3 нГн; J = ±5%; К = ±10%; М = ±20%.

Цветовую маркировку можно распознать аналогично таковой на резисторах. Воспользуйтесь таблицей, чтобы расшифровать цветные полосы или кольца на элементе. Первое кольце иногда делают шире остальных.

На это мы и заканчиваем рассматривать, что собой представляет катушка индуктивности, из чего она состоит и зачем нужна. Напоследок рекомендуем посмотреть полезное видео по теме статьи:

Материалы по теме:

• Как сделать индукционный котел своими руками
• Что такое самоиндукция
• Калькулятор для расчета катушки индуктивности

Теоретическое обоснование

Если в проводящем контуре течёт ток, то ток создаёт магнитное поле.

Будем вести рассмотрение в квазистатическом приближении, подразумевая, что переменные электрические поля достаточно слабы либо меняются достаточно медленно, чтобы можно было пренебречь порождаемыми ими магнитными полями.

Ток считаем одинаковым по всей длине контура (пренебрегая ёмкостью проводника, которая позволяет накапливать заряды в разных его участках, что вызвало бы неодинаковость тока вдоль проводника и заметно усложнило бы картину).

По закону Био — Савара — Лапласа, величина вектора магнитной индукции, создаваемой некоторым элементарным (в смысле геометрической малости участка проводника, рассматриваемого как элементарный источник магнитного поля) током в каждой точке пространства, пропорциональна этому току. Суммируя поля, создаваемые каждым элементарным участком, приходим к тому, что и магнитное поле (вектор магнитной индукции), создаваемое всем проводником, также пропорционально порождающему току.

Рассуждение выше верно для вакуума. В случае присутствия магнитной среды (магнетика) с заметной (или даже большой) магнитной восприимчивостью, вектор магнитной индукции (который и входит в выражение для магнитного потока) будет заметно (или даже во много раз) отличаться от того, каким бы он был в отсутствие магнетика (в вакууме). Мы ограничимся здесь линейным приближением, тогда вектор магнитной индукции, хотя, возможно, возросший (или уменьшившийся) в заметное количество раз по сравнению с отсутствием магнетика при том же контуре с током, тем не менее остаётся пропорциональным порождающему его току.

Тогда магнитный поток, то есть поток поля вектора магнитной индукции:

Φ=∫SB⋅dS{\displaystyle \Phi =\int \limits _{S}\mathbf {B} \cdot \mathbf {dS} }

через любую конкретную фиксированную поверхность S (в частности и через интересующую нас поверхность, краем которой является наш контур с током) будет пропорционален току, так как пропорционально току B всюду под интегралом.

Заметим, что поверхность, краем которой является контур, может быть достаточно сложна, если сложен сам контур. Уже для контура в виде просто многовитковой катушки такая поверхность оказывается достаточно сложной. На практике это приводит к использованию некоторых упрощающих представлений, позволяющих легче представить такую поверхность и приближённо рассчитать поток через неё (а также в связи с этим вводятся некоторые дополнительные специальные понятия, подробно описанные в отдельном параграфе ниже). Однако здесь, при чисто теоретическом рассмотрении нет необходимости во введении каких-то дополнительных упрощающих представлений, достаточно просто заметить, что как бы ни был сложен контур, в данном параграфе мы имеем в виду «полный поток» — то есть поток через всю сложную (как бы многолистковую) поверхность, натянутую на все витки катушки (если речь идет о катушке), то есть о том, что называется потокосцеплением. Но поскольку нам здесь не надо конкретно рассчитывать его, а нужно только знать, что он пропорционален току, нам не слишком интересен конкретный вид поверхности, поток через которую нас интересует (ведь свойство пропорциональности току сохраняется для любой).

Итак, мы обосновали:

Φ {\displaystyle \Phi \ }~ I,{\displaystyle \ I,}

этого достаточно, чтобы утверждать, введя обозначение L для коэффициента пропорциональности, что

Φ=LI.{\displaystyle \Phi =LI.}

В заключение теоретического обоснования покажем, что рассуждение корректно в том смысле, что магнитный поток не зависит от конкретной формы поверхности, натянутой на контур. (Действительно, даже на самый простой контур может быть натянута — в том смысле, что контур должен быть её краем — не единственная поверхность, а разные, например, начав с двух совпадающих поверхностей, затем одну поверхность можно немного прогнуть, и она перестанет совпадать со второй). Поэтому надо показать, что магнитный поток одинаков для любых поверхностей, натянутых на один и тот же контур.

Но это действительно так: возьмём две такие поверхности. Вместе они будут составлять одну замкнутую поверхность. А мы знаем (из закона Гаусса для магнитного поля), что магнитный поток через любую замкнутую поверхность равен нулю. Это (с учетом знаков) означает, что поток через одну поверхность и другую поверхность — равны. Что доказывает корректность определения.

Влияние числа витков и способа намотки

Катушка индуктивности – это спираль, созданная из проводящего материала. Рабочие параметры изделий будут зависеть от особенностей конструкции. Индуктивность увеличивают:

• большим количеством витков на единицу длины;
• укрупнением поперечного сечения;
• установкой в центральной части сердечника с ферромагнитными характеристиками.

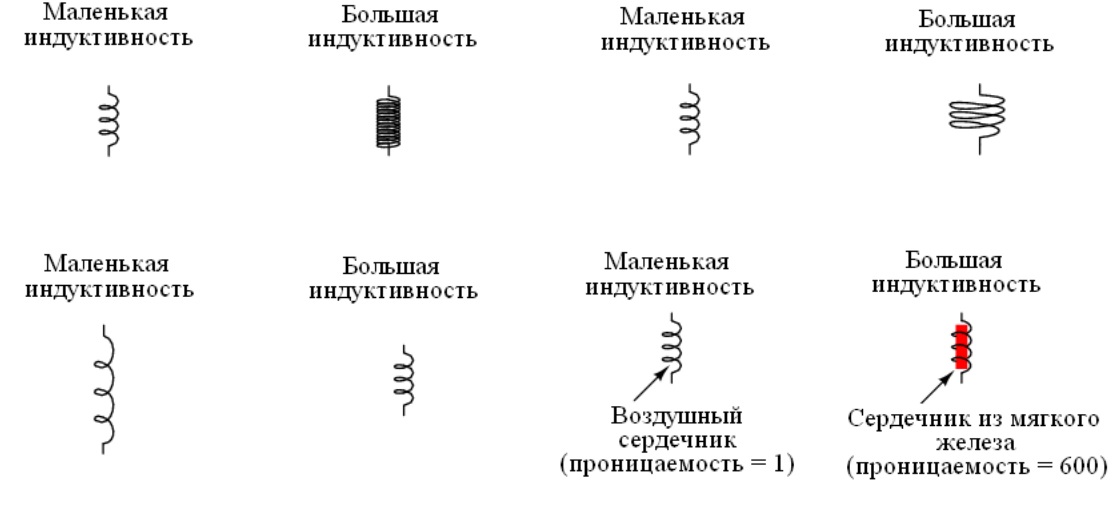От чего зависит индуктивность катушки, примеры типовых решений

Индуктивность одновиткового контура и индуктивность катушки

Для расчета элементарной конструкции подойдет преобразованная первая формула:

Ф = L * I.

Если рассматривается катушка, это выражение трансформируют в суммарное выражение магнитных потоков (Ψ), образованных отдельными витками:

Ψ = n * Ф.

Аналогичным образом:

Ln = L1 * n.

В действительности для точных расчетов учитывают различия силовых линий в центральной части и на краях конструкции. Для коррекции применяют более сложные выражения.

Индуктивность соленоида

Достаточно длинная электрическая катушка формирует внутри параллельные силовые линии. Для создания равномерного распределения энергии необходимо применять проводник с толщиной намного меньше, по сравнению с диаметром поперечного сечения. Разумеется, необходимо установить одинаковое расстояние между отдельными витками.

Такую конструкцию называют соленоидом. Плотность магнитного потока (B) в центральной рабочей части будет зависеть прямо пропорционально от длины (l) и следующих параметров:

• количества витков (N);
• тока (i);
• плотности намотки (n – число контуров на единицу длины);
• площади поперечного сечения (S);
• объема (V = S * l).

Ниже приведены основные формулы для вычислений при отсутствии сердечника с учетом магнитной постоянной (m ≈ 1,257 *10-6 Гн/ м):

• В = m0 * N * (i/l) = m0 * n * I;
• Ψ = m0 * N2 * (I * S/l) = m0 * n2 * i *V;
• L = m0 * N2 * (S/l) = m0 * n2 * V.

Индуктивность тороидальной катушки (катушки с кольцевым сердечником)

Для вычисления индукции катушки с сердечником в представленные выше формулы добавляют корректирующий множитель «m». С учетом особой формы изделия необходимо сделать следующие изменения:

L = N2 * ((m0 * m * S)/2π * rL), либо L = N2 * ((m0 * m * h)/2π) * ln(R/r),

где:

• 2π * rL – длина рабочего элемента со средним радиусом rL;
• R (r) и h – наружный (внутренний) радиус и высота тора, соответственно.

Коэффициентом «m» учитывают относительный показатель магнитной проницаемости определенного материала к значению для нейтральной среды (вакуума). Если m намного больше единицы, допускается не учитывать искажения поля, которые создает толстый проводник.

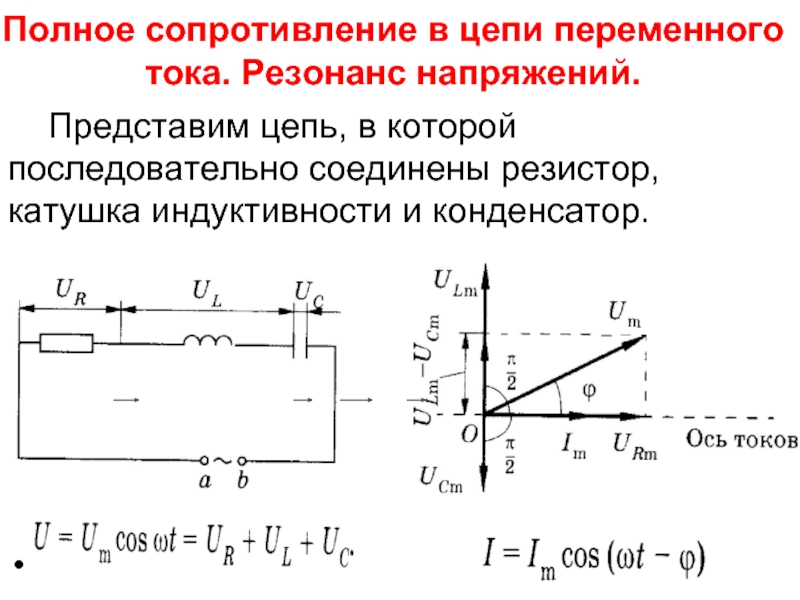
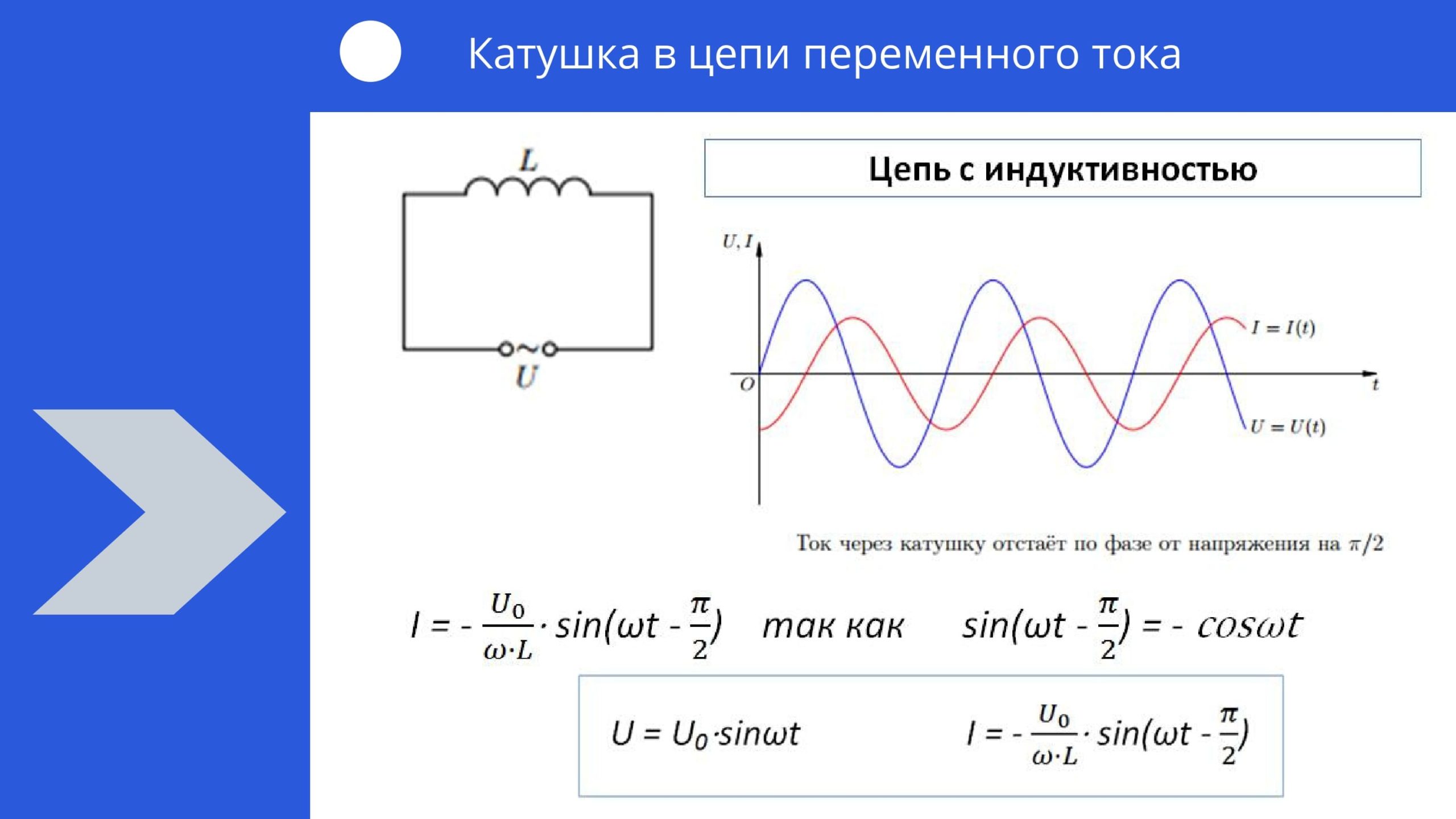
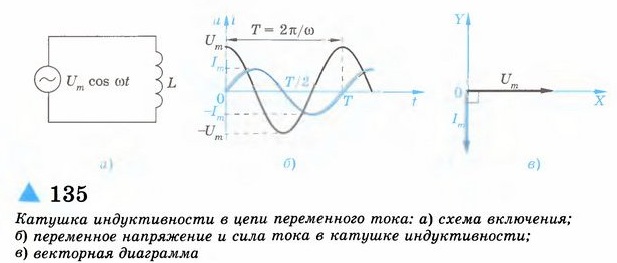
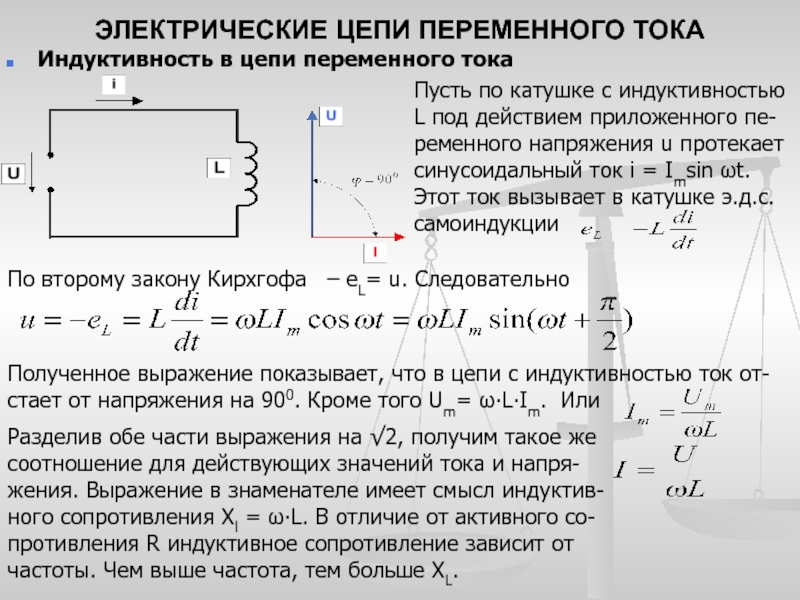
Индуктивность и емкость в цепи переменного тока

Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальные фазы напряжения и э. д. с. соответственно будут иметь некоторые значения ϕ и ψ. При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:

i = Iм sin ωt

u = Uм sin (ϕ + ωt),

e = Ɛm sin (ψ + ωt).

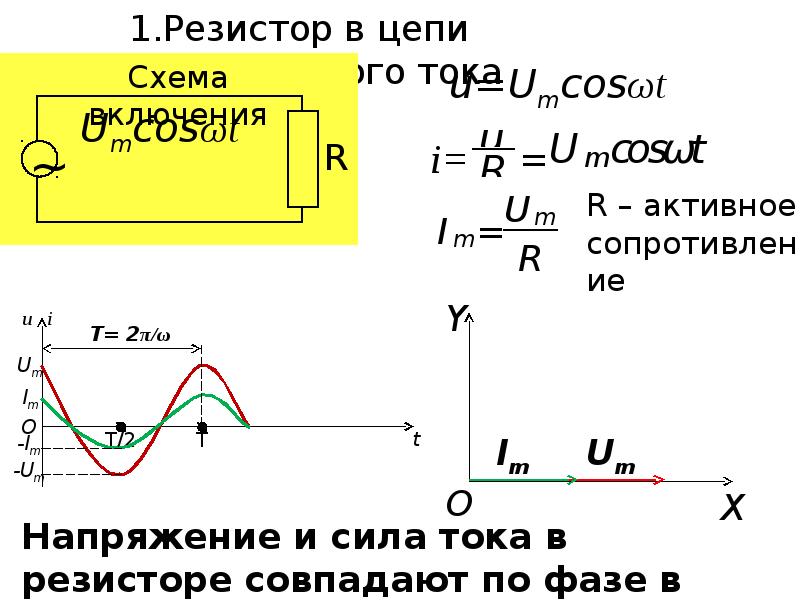
Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным. Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току и находить по формуле:

R=(pl/S)(1 + at).

В цепи переменного тока, имеющей только активное сопротивление, например в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. ϕ=0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.

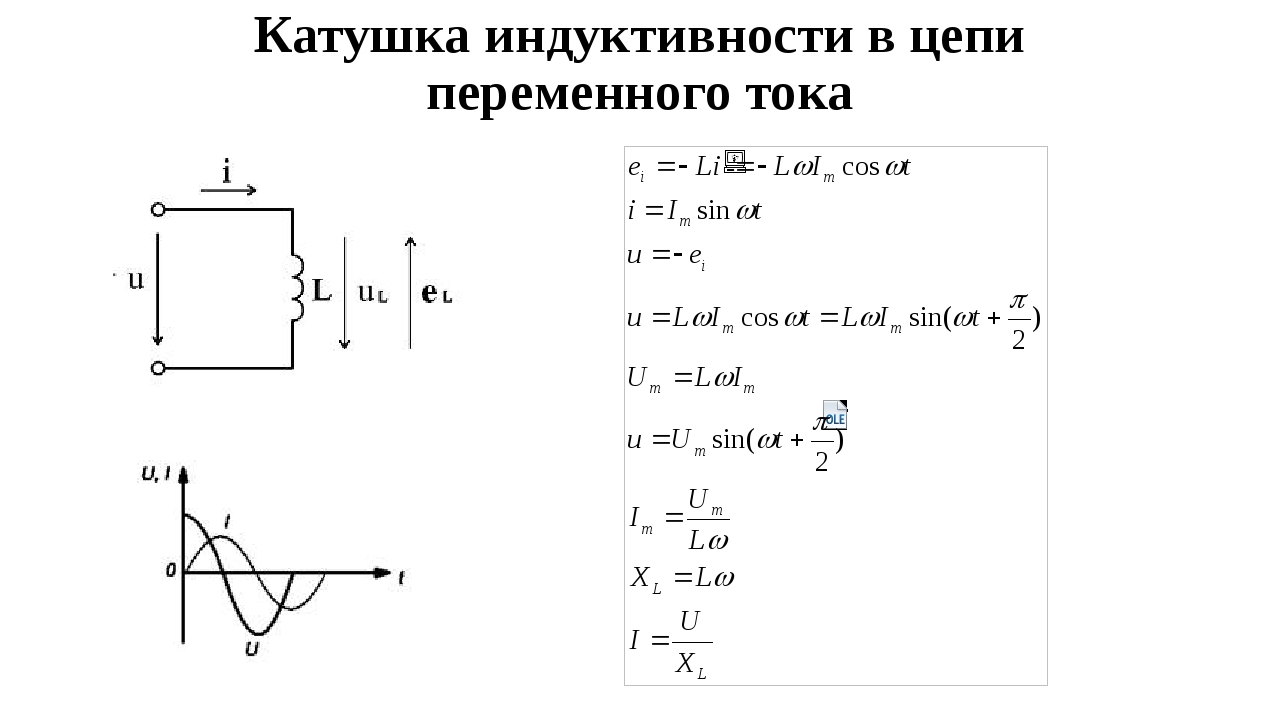
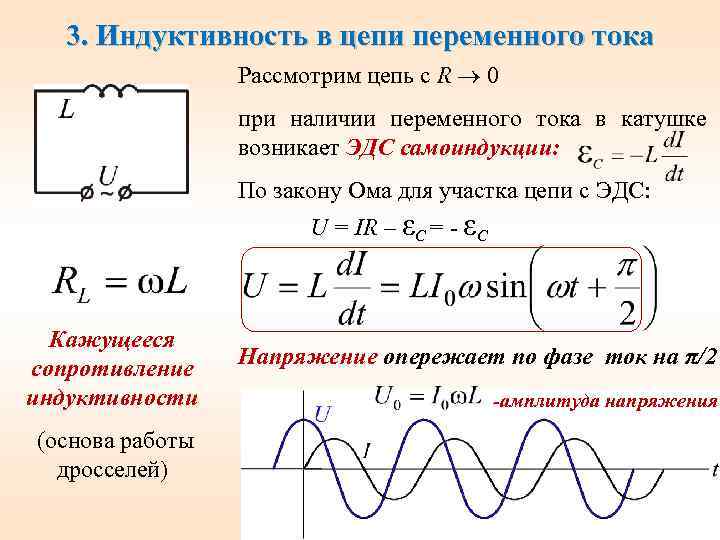
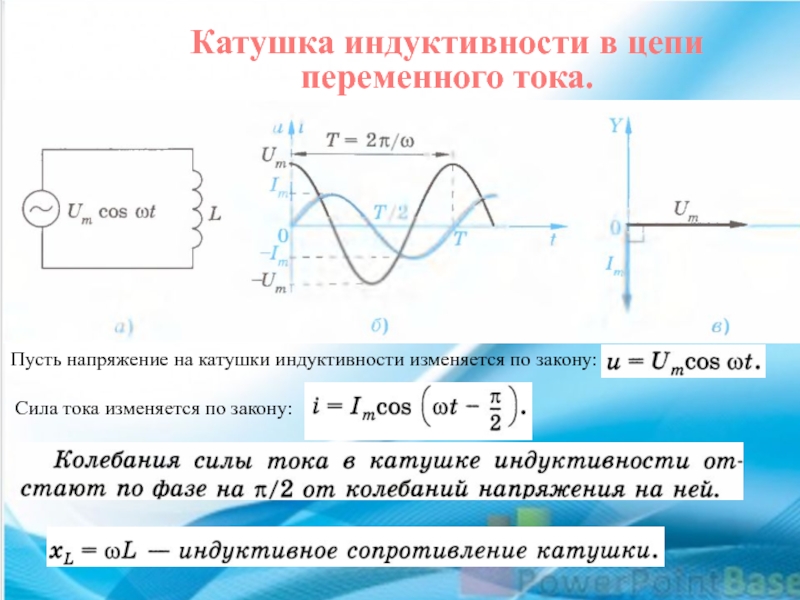
График и схема подключения

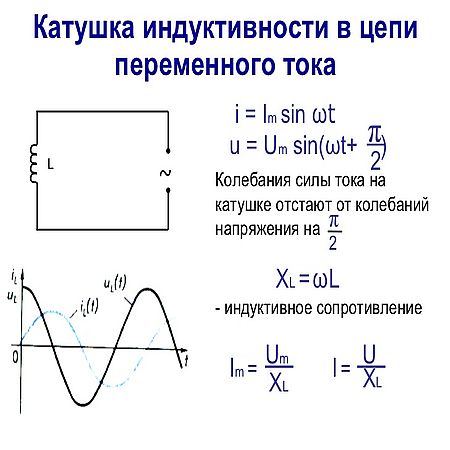
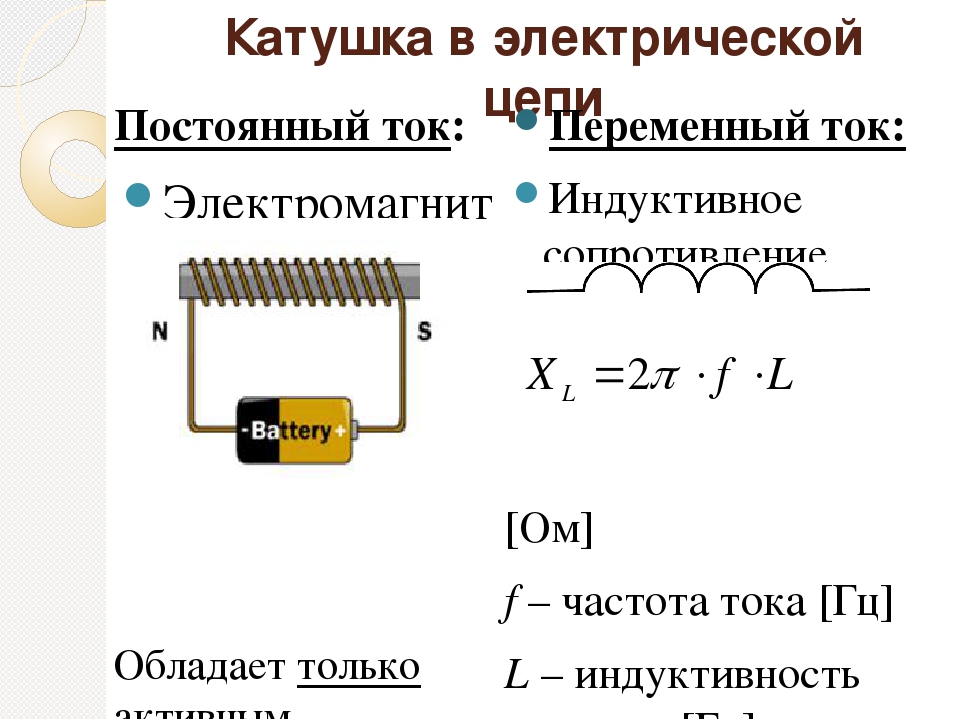
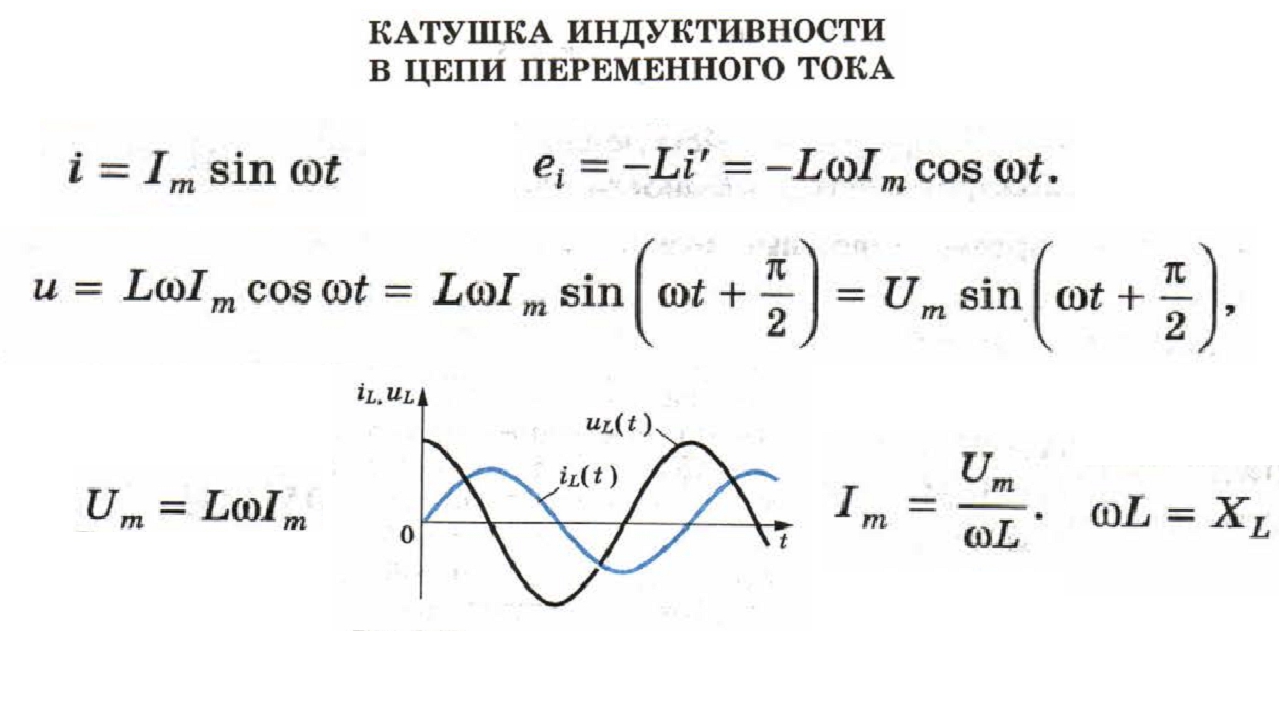
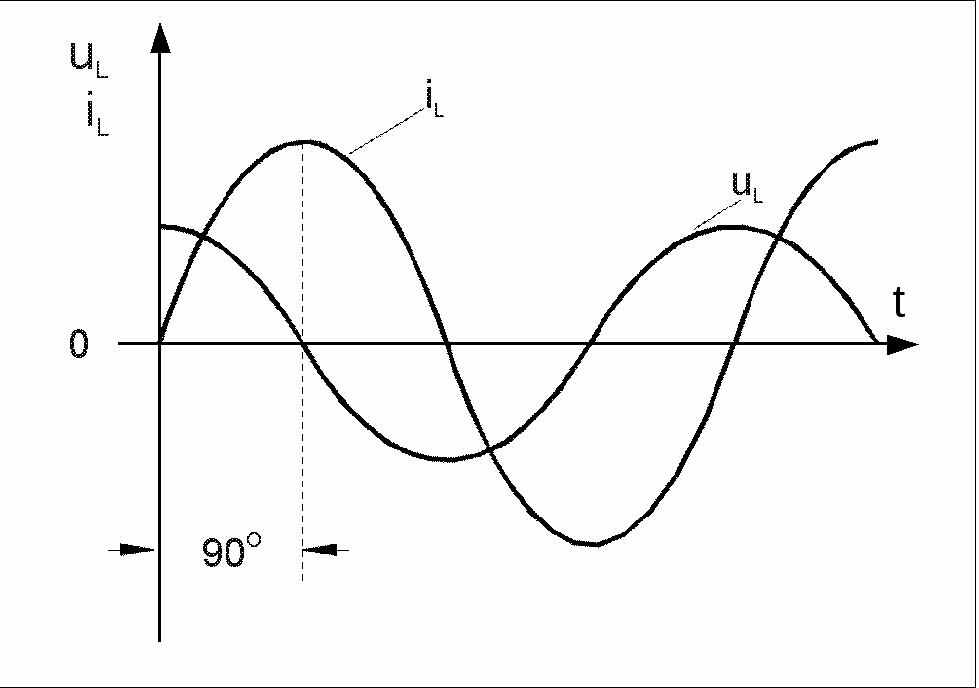
Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление X_L, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:

Х_L = ωL.

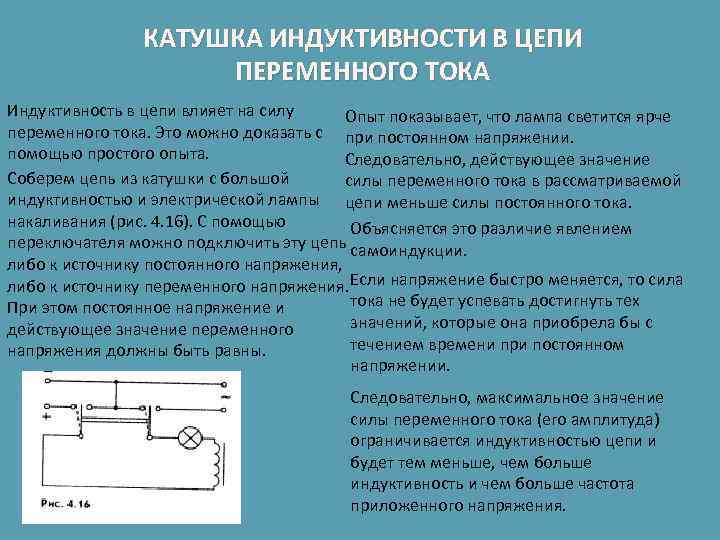
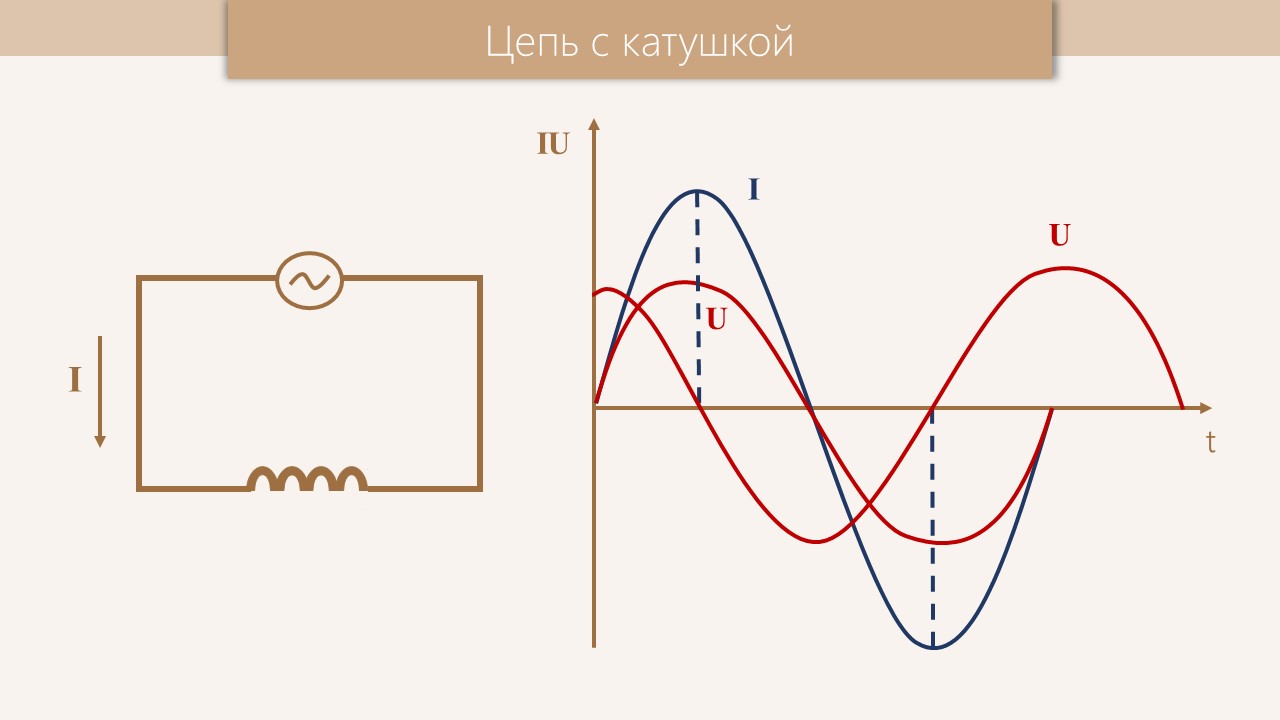
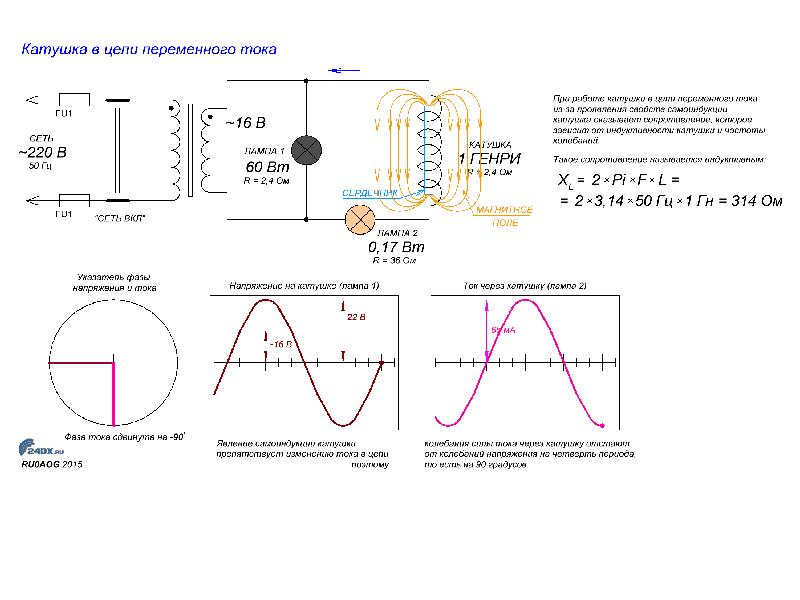
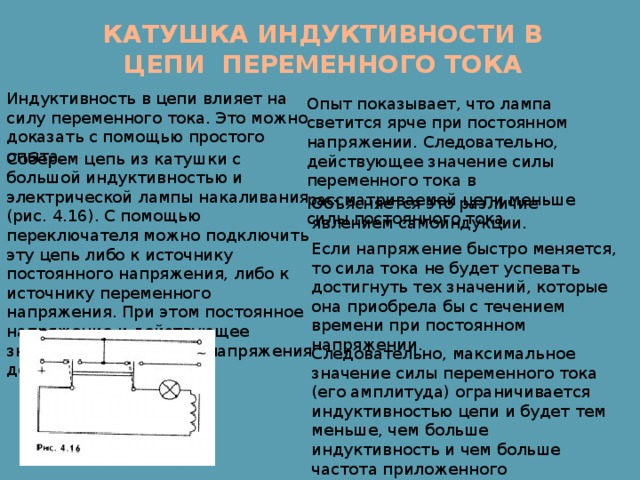
Влияние индуктивного сопротивления на силу тока в цепи наглядно иллюстрируется опытом, изображенным на рис. 26.6. При опускании ферромагнитного сердечника в катушку лампа гаснет, а при его удалении вновь загорается. Это объясняется тем, что индуктивность катушки сильно возрастает при введении в нее сердечника. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток.

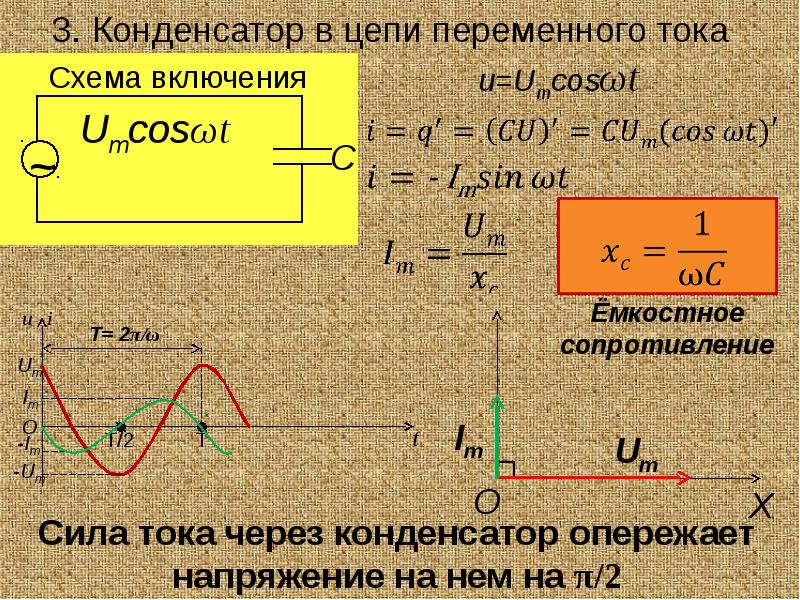
Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.

Катушки индуктивности

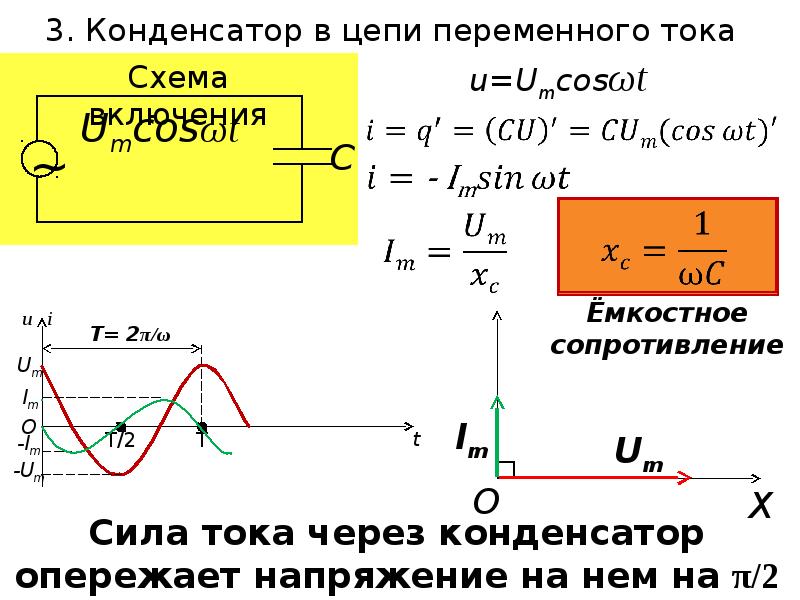
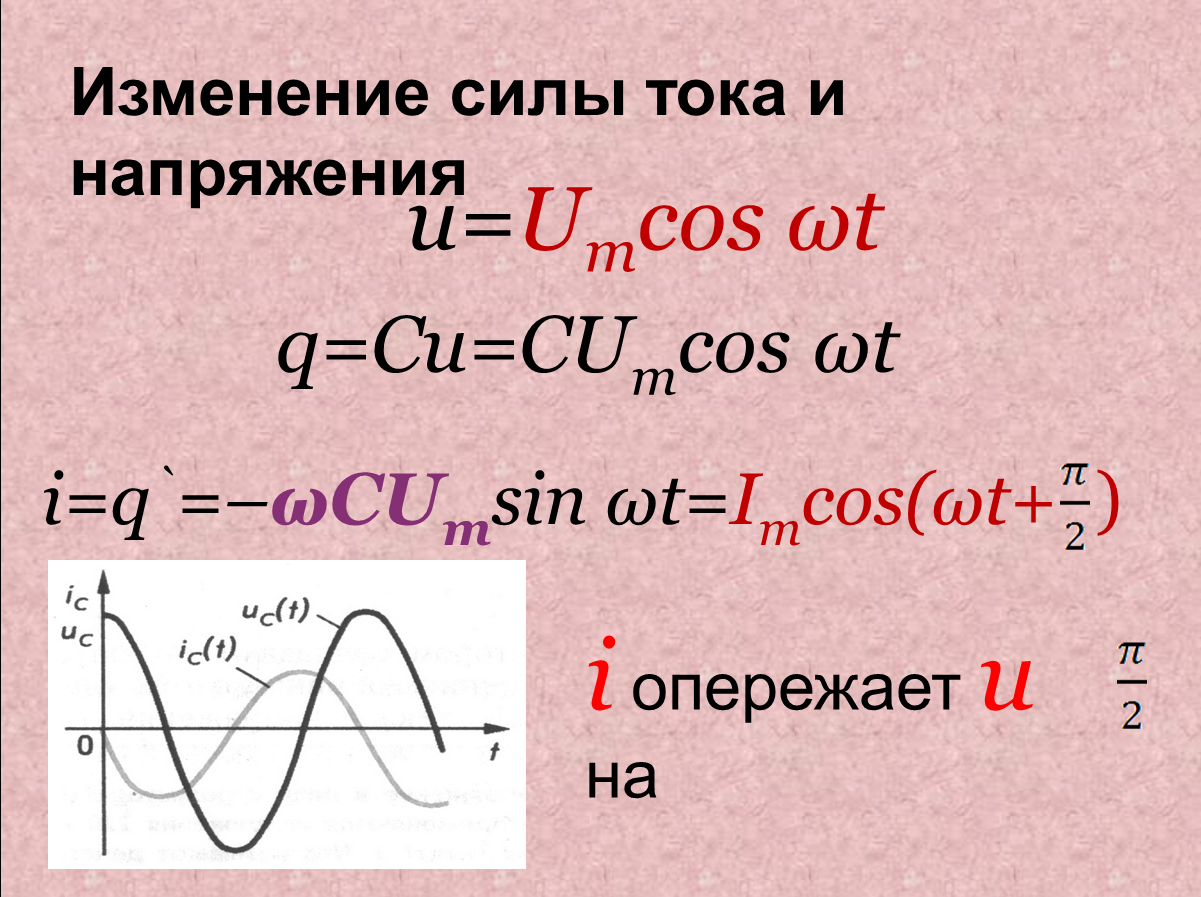
Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока. Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс. Оно обратно пропорционально емкости С и круговой частоте ω;

Хс = 1/ωС

Из сравнения формул (26.11) и (26.12) видно, что катушки индуктивности представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Напряжение на емкостном сопротивлении Ха отстает по фазе от тока. Индуктивное X_L и емкостное Хс сопротивления называют реактивными. В теории переменного тока доказывается, что при последовательном включении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:

X = X_L—X_C

и имеет индуктивный характер при X_L > Хс и емкостный характер при X_L 

В заключение заметим, что средняя активная мощность переменного тока, показывающая, сколько энергии за единицу времени передается электрическим током данному участку цепи, определяется формулой:

P = IU cos ϕ.

Мощность, затрачиваемая только на тепловое действие тока, выражается формулой:

Р = I2R

Для увеличения активной мощности переменного тока нужно повышать cos ϕ. (Объясните, почему наибольшее значение cos ϕ имеет при X_L=X_C.)

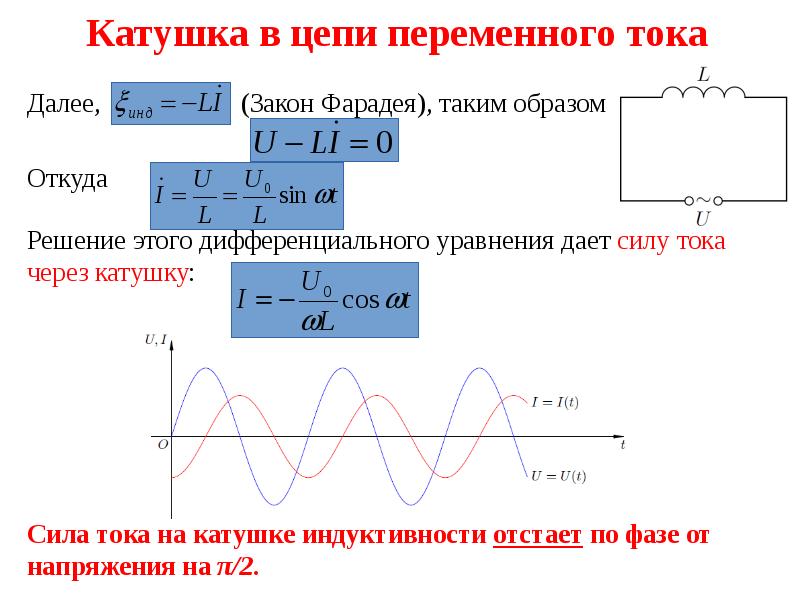
Индуктивность

Самоиндукция

Если через замкнутый контур пропускать переменный ток, можно зарегистрировать с помощью простых экспериментов магнитное поле в окружающей среде. Изменение силовых параметров сопровождается появлением в цепи наведенной электродвижущей силы. Данное явление называют самоиндукцией.

Величину ЭДС можно вычислить по формуле:

Е = -L * (Δi/Δt).

Это выражение показывает зависимость напряжения от изменения тока за единицу времени. Поправочный коэффициент (L) обозначает особенности проводника (индукционной катушки). Знак «-» характеризует инерционные свойства явления.

При пропускании синусоидального сигнала следует учитывать отставание напряжения (векторное выражение) от тока на 90 градусов. Амплитуда будет прямо пропорциональна частоте (w):

E = L * I * w.

Виды и типы катушек

В зависимости от сферы применения и частоты цепи может отличаться конструкция катушки.

По частоте можно условно разделить на:

• Низкочастотные. Пример — дроссель люминесцентной лампы, трансформатор (каждая обмотка представляет собой катушку индуктивности), реактор, фильтры электромагнитных помех. Сердечники чаще всего выполняются из электротехнической стали, для цепей переменного тока из листов (шихтованный сердечник).

• Высокочастотные. Например, контурные катушки радиоприемников, катушки связи усилителей сигнала, накопительные и сглаживающие дроссели импульсных блоков питания. Их сердечник изготавливают обычно из феррита.

Конструкция отличается в зависимости от характеристик катушки, например, намотка может быть однослойной и многослойной, намотанной виток к витку или с шагом. Шаг между витками может быть постоянным или прогрессивным (изменяющимся по длине катушки). Способ намотки и конструкция влияют на конечные размеры изделия.

Отдельно стоит рассказать о том, как устроена катушка с переменной индуктивностью, их еще называют вариометры. На практике можно встретить разные решения:

• Сердечник может двигаться относительно обмотки.
• Две обмотки расположены на одном сердечнике и соединены последовательно, при их перемещении изменяется взаимоиндукция и индуктивная связь.
• Сами витки для настройки контура могут раздвигаться или сужаться приближаясь друг к другу (чем плотнее намотка — тем больше индуктивность).

И так далее. При этом подвижная часть называется ротором, а неподвижная — статором.

По способу намотки бывают также различными, например, фильтры со встречной намоткой подавляют помехи из сети, а намотанные в одну сторону (согласованная намотка) подавляют дифференциальные помехи.