- Зависимость от температуры
- Что такое электрическое сопротивление?
- Связь с удельной проводимостью
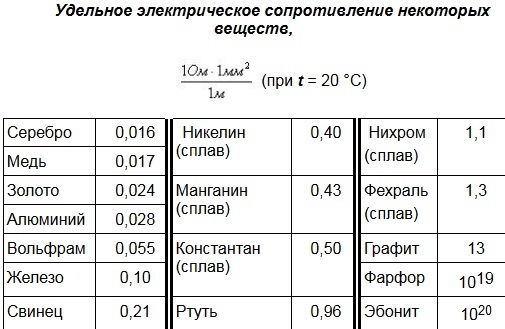
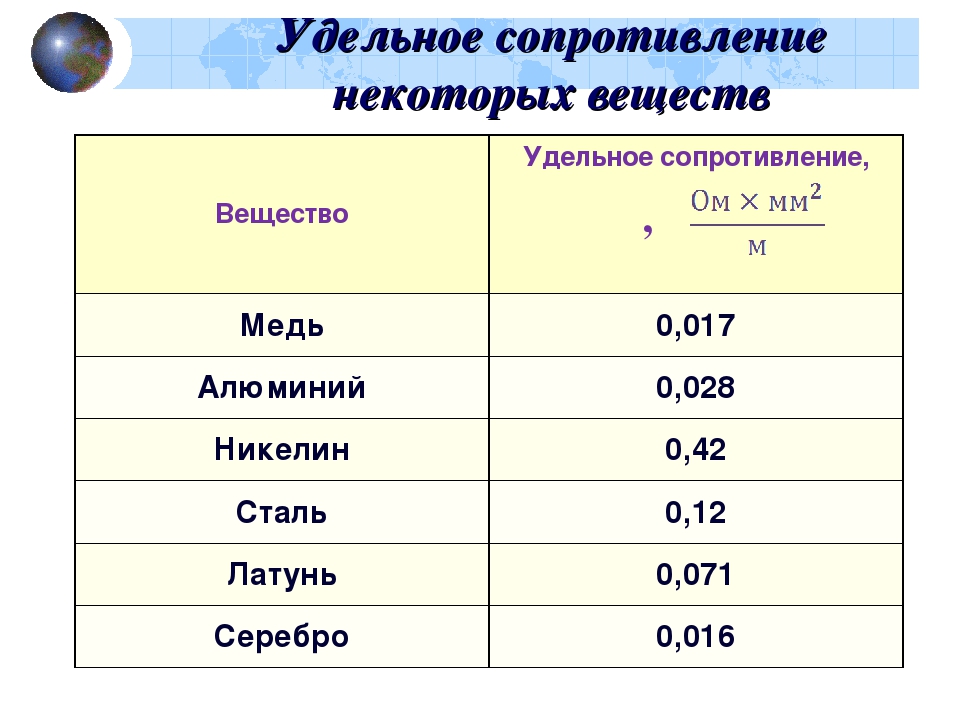
- Таблица удельного электрического сопротивления некоторых металлов
- Понятие электрического сопротивления проводника
- От чего и как зависит сопротивление?
- Что такое сопротивление медного провода
- Температурная зависимость ρ(Т)
- Что мы узнали?
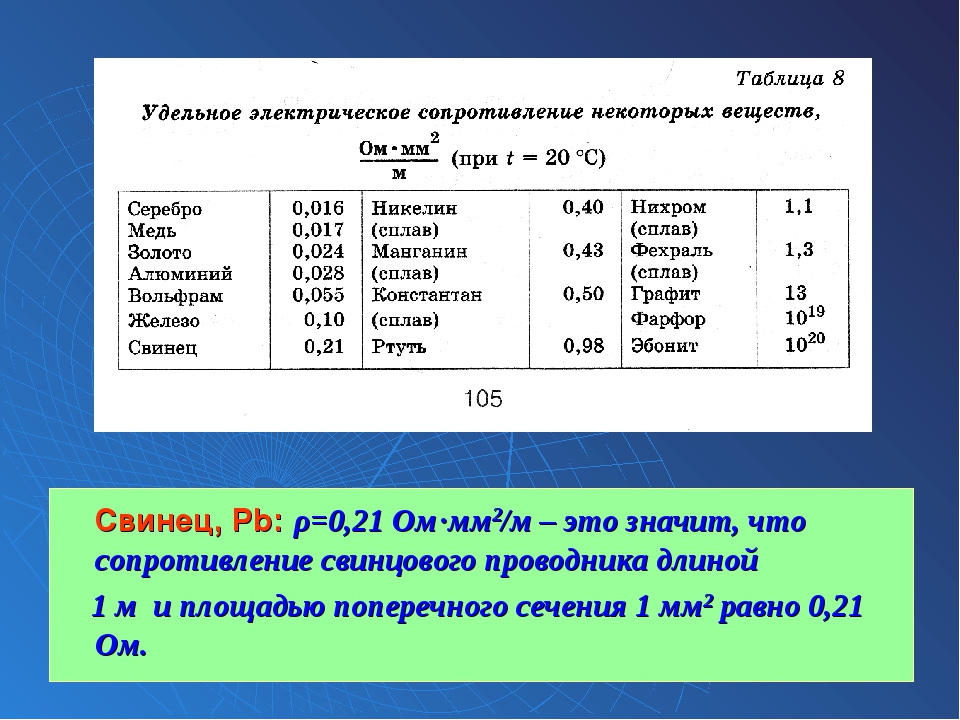
- Удельное электрическое сопротивление
- Что мы узнали?
- Таблица сопротивления металлов
- Тонкие плёнки
Зависимость от температуры
Удельное электрическое сопротивление зависит от температуры. Но все группы веществ проявляют себя по-разному при ее изменении. Это необходимо учитывать при расчете проводов, которые будут работать в определенных условиях. К примеру, на улице, где значения температуры зависят от времени года, необходимые материалы с меньшей подверженностью изменениям в диапазоне от -30 до +30 градусов Цельсия. Если же планируется применение в технике, которая будет работать в одних и тех же условиях, то здесь также нужно оптимизировать проводку под конкретные параметры. Материал всегда подбирается с учетом эксплуатации.
В номинальной таблице удельное электрическое сопротивление берется при температуре 0 градусов Цельсия. Повышение показателей данного параметра при нагреве материала обусловлено тем, что интенсивность передвижения атомов в веществе начинает возрастать. Носители электрических зарядов хаотично рассеиваются во всех направлениях, что приводит к созданию препятствий при передвижении частиц. Величина электрического потока снижается.
При уменьшении температуры условия прохождения тока становятся лучше. При достижении определенной температуры, которая для каждого металла будет отличаться, появляется сверхпроводимость, при которой рассматриваемая характеристика почти достигает нуля.
Отличия в параметрах порой достигают очень больших значений. Те материалы, которые обладают высокими показателями, могут использовать в качестве изоляторов. Они помогают защищать проводку от замыкания и ненамеренного контакта с человеком. Некоторые вещества вообще не применимы для электротехники, если у них высокое значение этого параметра. Этому могут мешать другие свойства. Например, удельная электрическая проводимость воды не будет иметь большого значения для данный сферы. Здесь приведены значения некоторых веществ с высокими показателями.
| Материалы с высоким удельным сопротивлением | ρ (Ом·м) |
| Бакелит | 1016 |
| Бензол | 1015…1016 |
| Бумага | 1015 |
| Вода дистиллированная | 104 |
| Вода морская | 0.3 |
| Дерево сухое | 1012 |
| Земля влажная | 102 |
| Кварцевое стекло | 1016 |
| Керосин | 1011 |
| Мрамор | 108 |
| Парафин | 1015 |
| Парафиновое масло | 1014 |
| Плексиглас | 1013 |
| Полистирол | 1016 |
| Полихлорвинил | 1013 |
| Полиэтилен | 1012 |
| Силиконовое масло | 1013 |
| Слюда | 1014 |
| Стекло | 1011 |
| Трансформаторное масло | 1010 |
| Фарфор | 1014 |
| Шифер | 1014 |
| Эбонит | 1016 |
| Янтарь | 1018 |
Более активно в электротехнике применяются вещества с низкими показателями. Зачастую это металлы, которые служат проводниками. В них также наблюдается много различий. Чтобы узнать удельное электрическое сопротивление меди или других материалов, стоит посмотреть в справочную таблицу.
| Материалы с низким удельным сопротивлением | ρ (Ом·м) |
| Алюминий | 2.7·10-8 |
| Вольфрам | 5.5·10-8 |
| Графит | 8.0·10-6 |
| Железо | 1.0·10-7 |
| Золото | 2.2·10-8 |
| Иридий | 4.74·10-8 |
| Константан | 5.0·10-7 |
| Литая сталь | 1.3·10-7 |
| Магний | 4.4·10-8 |
| Манганин | 4.3·10-7 |
| Медь | 1.72·10-8 |
| Молибден | 5.4·10-8 |
| Нейзильбер | 3.3·10-7 |
| Никель | 8.7·10-8 |
| Нихром | 1.12·10-6 |
| Олово | 1.2·10-7 |
| Платина | 1.07·10-7 |
| Ртуть | 9.6·10-7 |
| Свинец | 2.08·10-7 |
| Серебро | 1.6·10-8 |
| Серый чугун | 1.0·10-6 |
| Угольные щетки | 4.0·10-5 |
| Цинк | 5.9·10-8 |
| Никелин | 0,4·10-6 |
Что такое электрическое сопротивление?
Ему можно дать определение исходя из двух позиций. Первая связана с формулой для закона Ома. И звучит оно так: электрическое сопротивление — это физическая величина, которая определяется как отношение напряжения в проводнике к силе тока, протекающего в нем. Математическая запись приведена немного ниже.
Вторая основывается на свойствах тела. Электрическое сопротивление проводника — это физическая величина, которая указывает на свойство тела преобразовывать энергию электричества в тепло. Оба этих утверждения верны. Только в школьном курсе чаще всего останавливаются на запоминании первого. Обозначается изучаемая величина буквой R. Единицы, в которых измеряется электрическое сопротивление, — Ом.
Связь с удельной проводимостью
В изотропных материалах связь между удельным сопротивлением ρ{\displaystyle \rho } и удельной проводимостью σ{\displaystyle \sigma } выражается равенством
- ρ=1σ.{\displaystyle \rho ={\frac {1}{\sigma }}.}
В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρij{\displaystyle \rho _{ij}} и тензора удельной проводимости σij{\displaystyle \sigma _{ij}} имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:
- Ji(r→)=∑j=13σij(r→)Ej(r→).{\displaystyle J_{i}({\vec {r}})=\sum _{j=1}^{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}
Из этого равенства и приведённого ранее соотношения для Ei(r→){\displaystyle E_{i}({\vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
- ρ11=1det(σ)σ22σ33−σ23σ32,{\displaystyle \rho _{11}={\frac {1}{\det(\sigma )}},}
- ρ12=1det(σ)σ33σ12−σ13σ32,{\displaystyle \rho _{12}={\frac {1}{\det(\sigma )}},}
где det(σ){\displaystyle \det(\sigma )} — определитель матрицы, составленной из компонент тензора σij{\displaystyle \sigma _{ij}}. Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1, 2 и 3.
Таблица удельного электрического сопротивления некоторых металлов
| Вид провода | ρ при 20℃, Ом-м |
| Серебряный | 1,59×10⁻⁸ |
| Медный | 1,67×10⁻⁸ |
| Золотой | 2,35×10⁻⁸ |
| Алюминиевый | 2,65×10⁻⁸ |
| Вольфрамовый | 5,65×10⁻⁸ |
| Никелевый | 6,84×10⁻⁸ |
| Железный | 9,7×10⁻⁸ |
| Платиновый | 1,06×10⁻⁷ |
| Стальной | 1,6×10⁻⁷ |
| Свинцовый | 2,06×10⁻⁷ |
| Дюралюминиевый | 4,0×10⁻⁷ |
| Нихромовый | 1,05×10⁻⁶ |
Удельное сопротивление абсолютно независимо от формы и размеров проводника, однако варьируется в широком диапазоне при отклонении температуры от принятого за стандартное значения, равного 20 градусам Цельсия. Практическим электротехническим путем доказано, что увеличение температуры повышает сопротивляемость металлов течению тока, с обратной стороны — вместе со снижением температуры она снижается. Примерно подсчитать, насколько существенным будет изменение, можно с учетом того, что всем металлам присущ почти одинаковый уровень прироста убыли данной величины, в среднем составляющий 0,4% на 1°С.
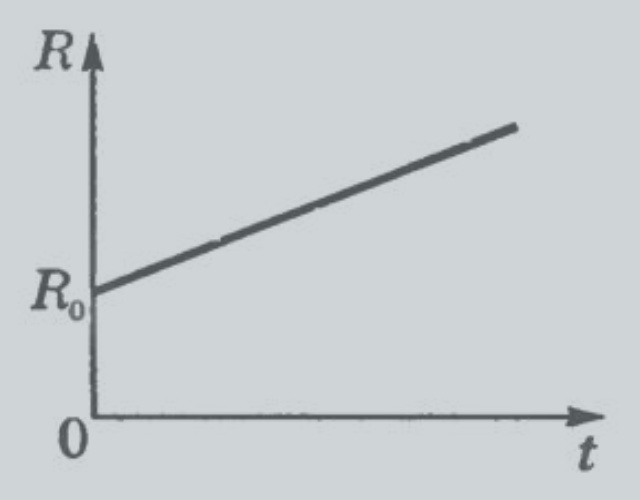 График сопротивления
График сопротивления
Если же данный показатель нужно определить точно, то можно воспользоваться этой формулой:
ρ = ρ0 x (1 + α x (t — t))
, где ρ и ρ0 — соответственно удельные сопротивления при температурах t и t (20°С, табличное значение), α — температурный коэффициент сопротивления.
| Вид провода | α |
| Никелевый | 0,005866 |
| Железный | 0,005671 |
| Молибденовый | 0,004579 |
| Вольфрамовый | 0,004403 |
| Алюминиевый | 0,004308 |
| Медный | 0,004041 |
| Серебряный | 0,003819 |
| Платиновый | 0,003729 |
| Золотой | 0,003715 |
| Цинковый | 0,003847 |
| Стальной | 0,003 |
| Нихромовый | 0,00017 |
Так, к примеру, найдя в таблицах удельное сопротивление меди при 20 градусах Цельсия и ее температурный коэффициент, можно вычислить, что при нагреве до 100℃ ее сопротивление вырастет на 32%. Практически то же самое будет происходить с удельным сопротивлением алюминиевого кабеля с тем же коэффициентом (0,004). А вот удельное сопротивление стали повысится менее значительно — на 24%.
 Нагрев
Нагрев
С увеличением температуры проводник насыщается тепловой энергией, передающейся всем атомам вещества. Этим обуславливается повышение интенсивности их теплового движения. Последний фактор и приводит к повышению сопротивляемости движению свободных электронов в определенном направлении, поскольку возрастает вероятность встречи свободных электронов с атомами. Когда температура снижается, меньшее количество атомов может препятствовать направленному движению электронов, следовательно, происходит обратное. В результате колоссального спада температуры возникает интереснейшее явление, называемое «сверхпроводимостью металлов»: сопротивляемость уменьшается до нуля в условиях, близких к абсолютному нулю (-273,15℃). В таких кондициях атомы металла замирают на своих позициях, и электроны движутся без каких-либо препятствий.
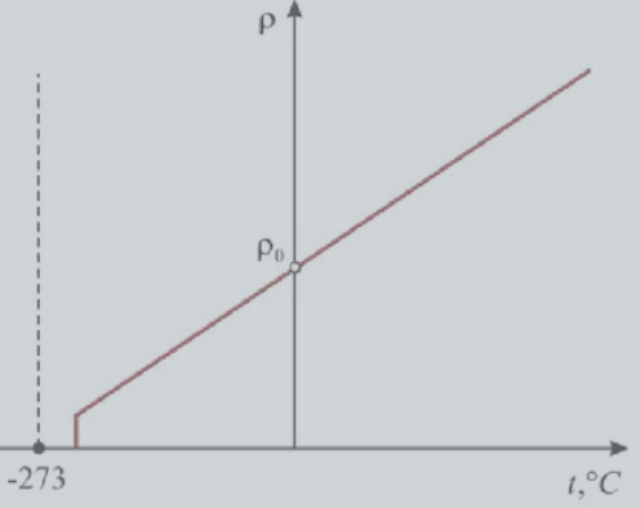 Сверхпроводимость
Сверхпроводимость
Понятие электрического сопротивления проводника
Классическое определение объясняет электрический ток движением «свободных» (валентных) электронов. Его обеспечивает созданное источником электрическое поле. Перемещение в металле затрудняют не только нормальные компоненты кристаллической решетки, но и дефектные участки, примеси, неоднородные области. В ходе столкновений с препятствиями за счет перехода импульса в тепловую энергию происходит повышение температуры.
 Наглядный пример – нагрев воды кипятильником
Наглядный пример – нагрев воды кипятильником
В газах, электролитах и других материалах несколько отличная физика явления. Линейные зависимости наблюдаются в металлах и других проводниках. Базовые соотношения выражены известной формулой закона Ома:
R (электрическое сопротивление) = U (напряжение)/ I (сила тока).
Для удобства часто используют обратную величину, проводимость (G = 1/R). Она обозначает способность определенного материала пропускать ток с определенными потерями.
Для упрощения иногда применяют пример с водопроводом. Движущаяся жидкость – аналог тока. Давление – эквивалент напряжения. Уменьшением (увеличением) поперечного сечения или положением запорного устройства определяют условия перемещения. Подобным образом изменяют основные параметры электрических цепей с помощью сопротивления (R).
К сведению. Количество жидкости, проходящее за единицу времени через контрольное сечение трубы, – эквивалент электрической мощности.
От чего и как зависит сопротивление?
Во-первых, от вещества, из которого изготовлен проводник. Чем больше значение, которое имеет удельное электрическое сопротивление, тем хуже он будет проводить ток.
Во-вторых, от длины провода. И здесь зависимость прямая. С увеличением длины сопротивление возрастает.
В-третьих, от толщины. Чем толще проводник, тем меньше у него сопротивление.
И наконец, в-четвертых, от температуры проводника. И здесь все не так однозначно. Если речь идет о металлах, то их электрическое сопротивление возрастает по мере нагревания. Исключение составляют некоторые специальные сплавы — их сопротивление практически не изменяется при нагревании. К ним относятся: константан, никелин и манганин. Когда же нагреваются жидкости, то их сопротивление уменьшается.

Что такое сопротивление медного провода
В металлах ток образуется при появлении электрического поля. Оно «заставляет» двигаться электроны упорядоченно, в одном направлении. Электроны дальних орбит атома, слабо удерживаемые ядром, формируют ток.
 Медные провода
Медные провода
При прохождении отрицательных частиц сквозь кристаллическую решетку молекул меди, они сталкиваются с атомами и другими электронами. Возникает препятствие или сопротивление направленному движению частиц.
Для оценки противодействия току была введена величина «электрическое сопротивление» или «электрический импеданс». Обозначается она буквой «R» или «r». Вычисляется сопротивление по формуле Георга Ома: R=, где U — разность потенциалов или напряжение, действующее на участке цепи, I — сила тока.
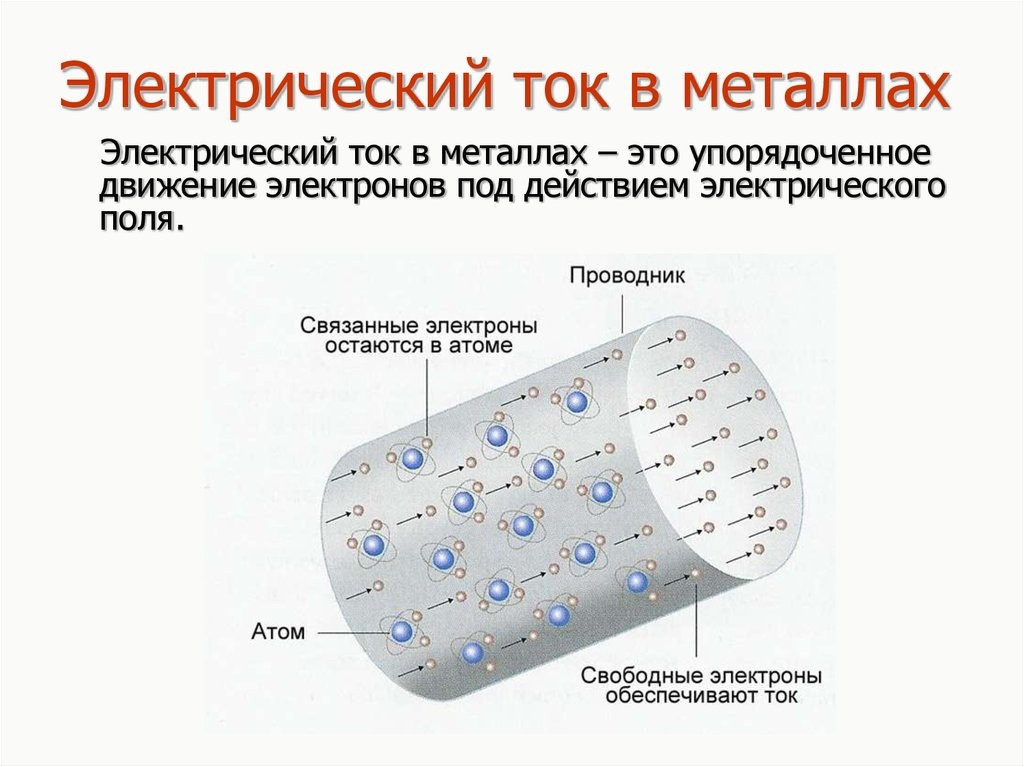 Понятие сопротивления
Понятие сопротивления
Важно! Чем выше значение импеданса металла, тем меньший ток проходит по нему, и именно медные проводники так широко распространены в электротехнике, благодаря этому свойству. Исходя из формулы Ома, на величину тока влияет приложенное напряжение при постоянном R
Но резистентность медных проводов меняется, в зависимости от их физических характеристик и условий эксплуатации
Исходя из формулы Ома, на величину тока влияет приложенное напряжение при постоянном R. Но резистентность медных проводов меняется, в зависимости от их физических характеристик и условий эксплуатации.
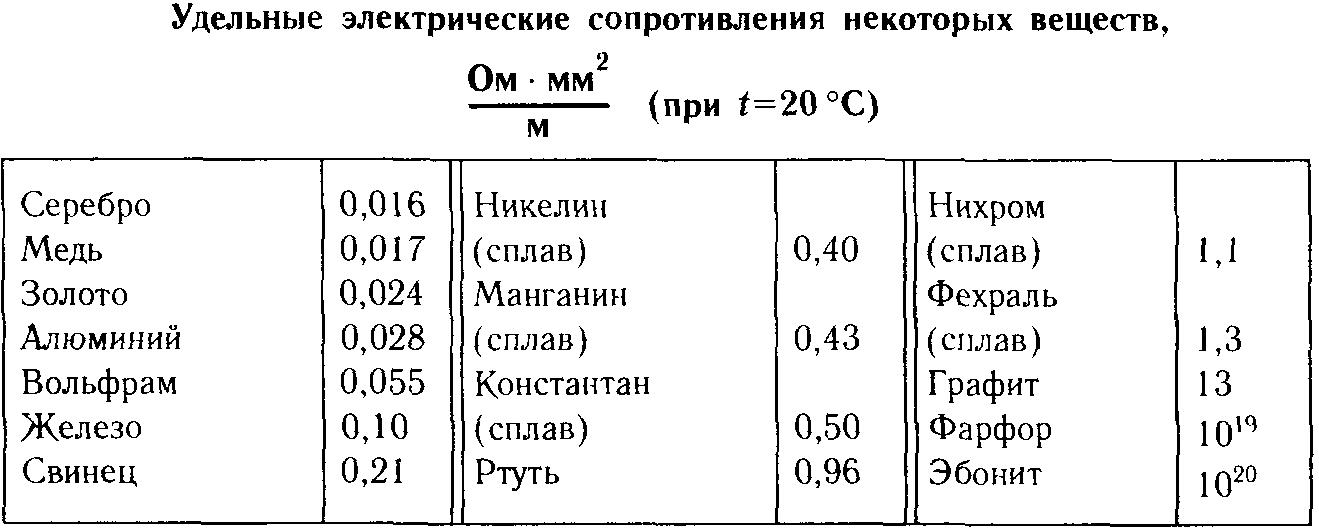
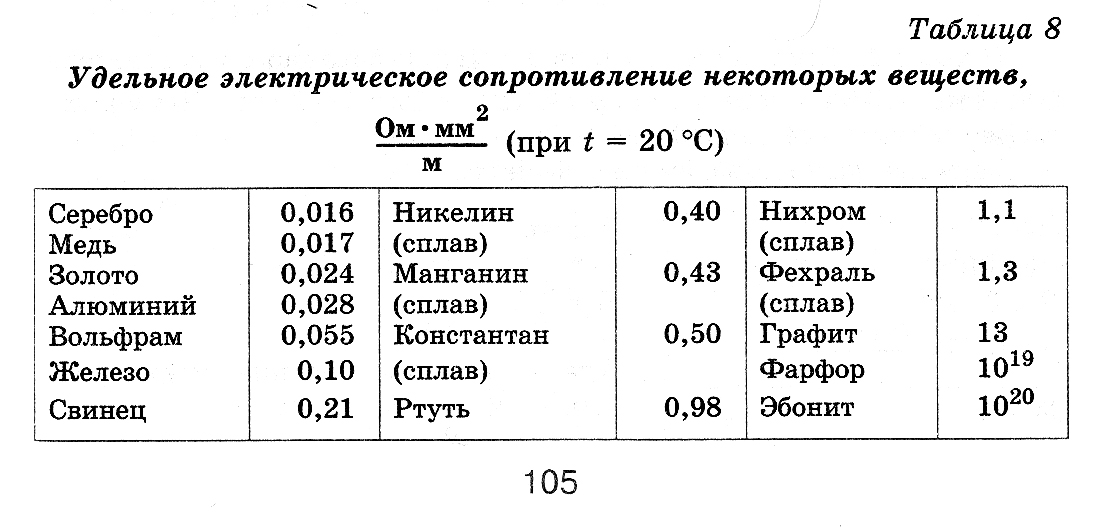
Температурная зависимость ρ(Т)
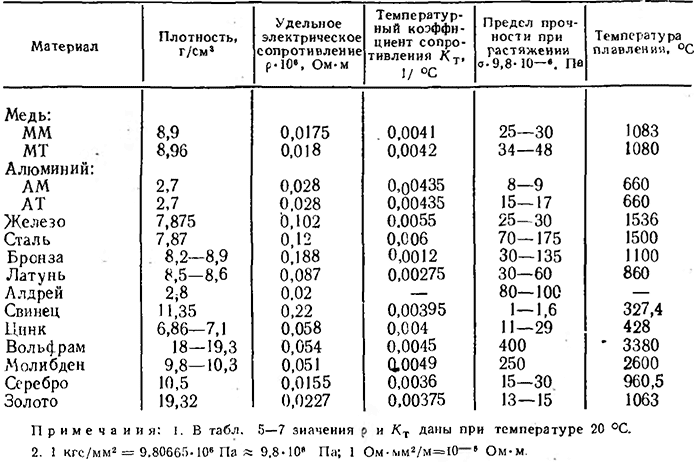
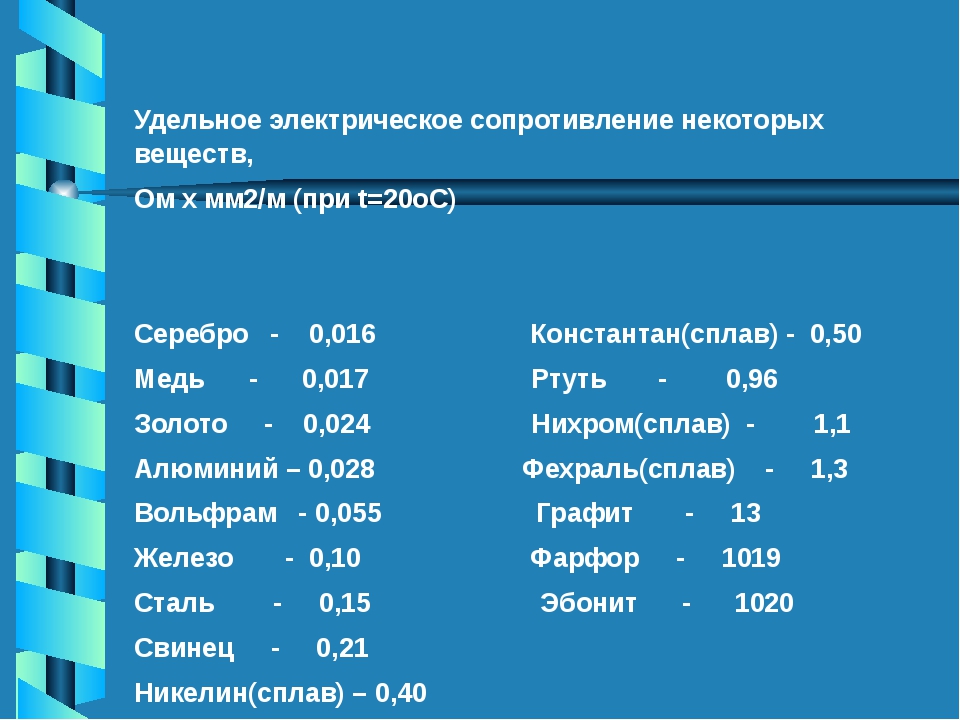
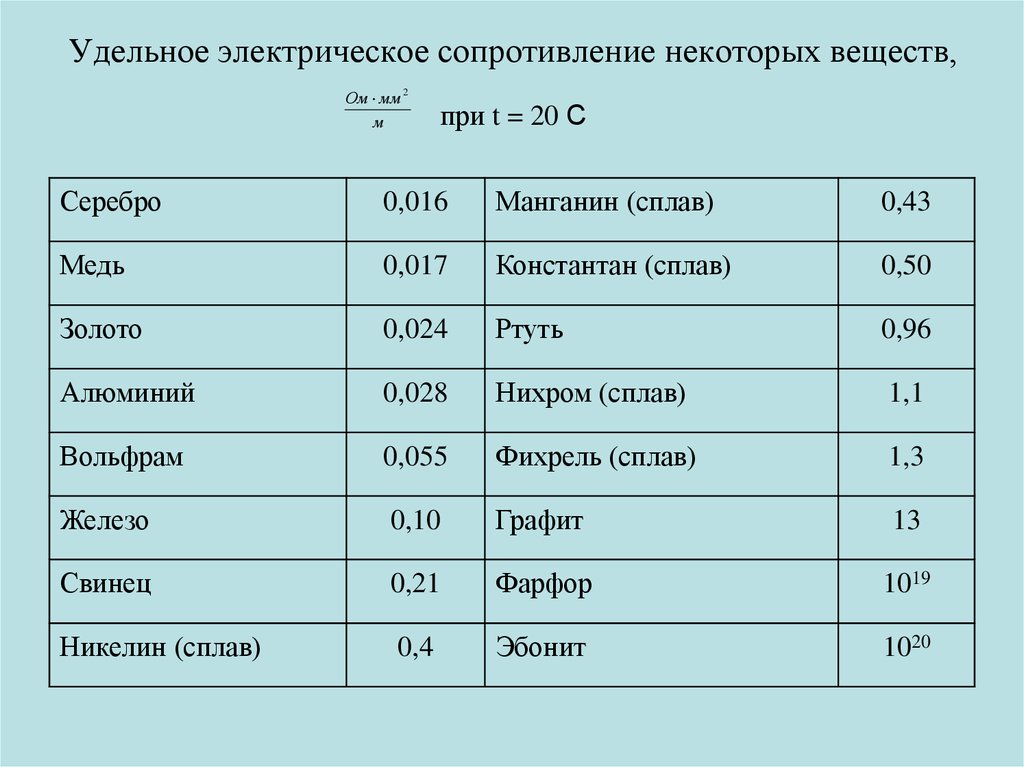
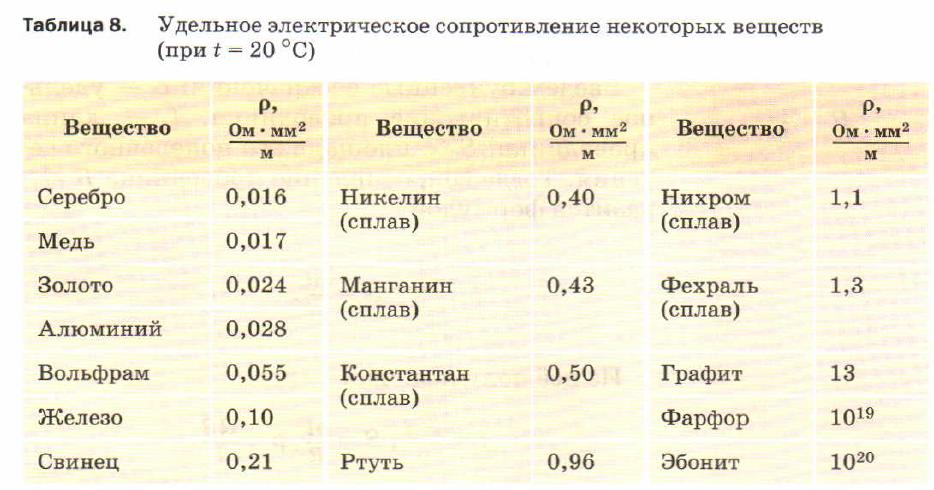
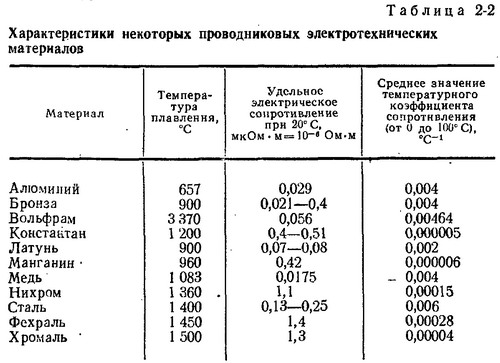
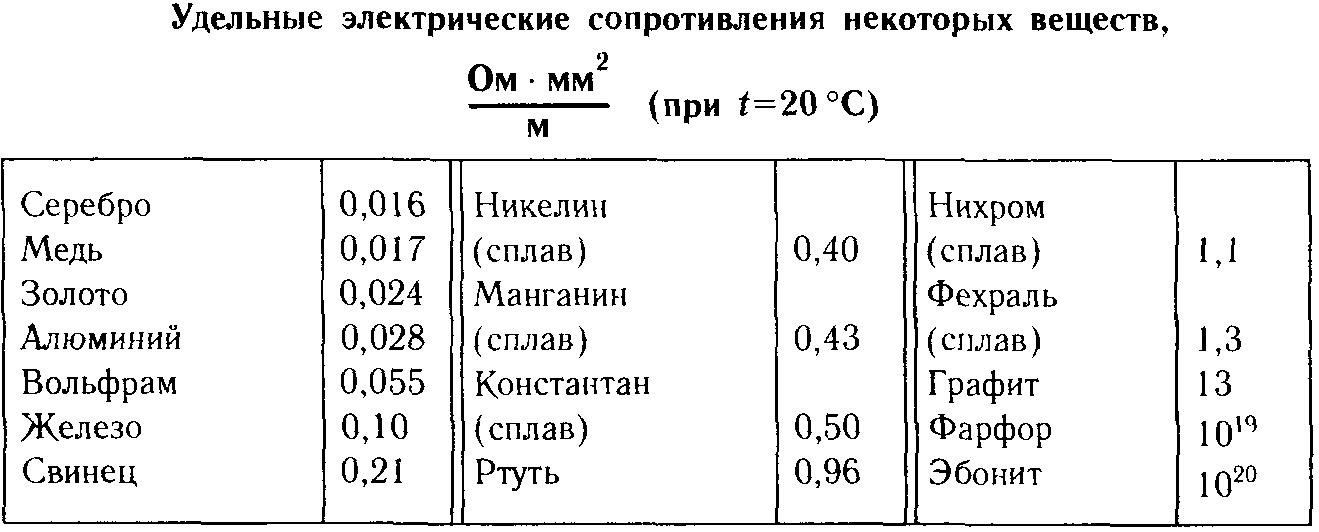
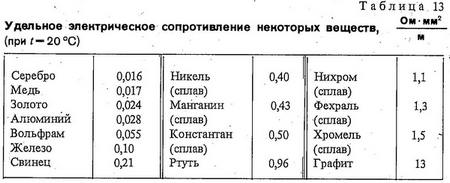
Для большинства материалов проведены многочисленные эксперименты по измерению значений удельных сопротивлений. Данные по большинству проводников можно найти в справочных таблицах.
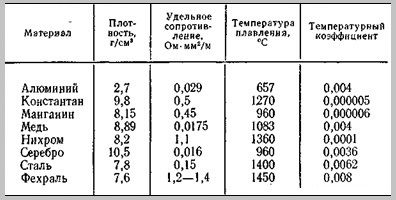
Удельное сопротивление металлов и сплавов, Ом*мм2/м
(при Т = 20С)
|
Серебро |
0,016 |
Бронза (сплав) |
0,1 |
|
Медь |
0,017 |
Олово |
0,12 |
|
Золото |
0,024 |
Сталь (сплав) |
0,12 |
|
Алюминий |
0,028 |
Свинец |
0,21 |
|
Иридий |
0,047 |
Никелин (сплав) |
0,42 |
|
Молибден |
0,054 |
Манганин (сплав) |
0,45 |
|
Вольфрам |
0,055 |
Константан (сплав) |
0,48 |
|
Цинк |
0,06 |
Титан |
0,58 |
|
Латунь (сплав) |
0,071 |
Ртуть |
0,958 |
|
Никель |
0,087 |
Нихром (сплав) |
1,1 |
|
Платина |
0,1 |
Висмут |
1,2 |
Чаще всего приводятся значения ρ при нормальной, то есть комнатной температуре 20С. Но оказалось, что при повышении температуры удельное сопротивление возрастает по линейному закону в соответствии с формулой:
$ ρ(Т) = ρ0 * (1 + α*T)$ (6),
где: ρ — удельное сопротивление проводника при температуре 0С, α — температурный коэффициент удельного сопротивления, который тоже имеет для каждого вещества свое, индивидуальное, значение. Из формулы (6) следует, что коэффициент α имеет размерность или .
Рис. 2. Температурная зависимость удельного сопротивления проводника
В соответствии с законом Джоуля-Ленца при протекании электрического тока т выделяется тепло, а значит происходит рост температуры проводника. Кроме этого, в зависимости от области применения, электрические приборы могут работать как при пониженных (минусовых), так и при высоких температурах. Для точных расчетов электрических цепей необходимо учитывать зависимость ρ(Т). Величину α для конкретного материала можно узнать из справочной литературы.
Рис. 3. Справочные значения температурного коэффициента удельного сопротивления проводников
Что мы узнали?
Итак, мы узнали, что величина, характеризующая способность различных материалов по разному проводить электрический ток, называется удельным электрическим сопротивлением. Приведена формула (3) для определения удельного сопротивления проводника ρ. Линейная температурная зависимость удельного сопротивления ρ(Т) описывается формулой (6).
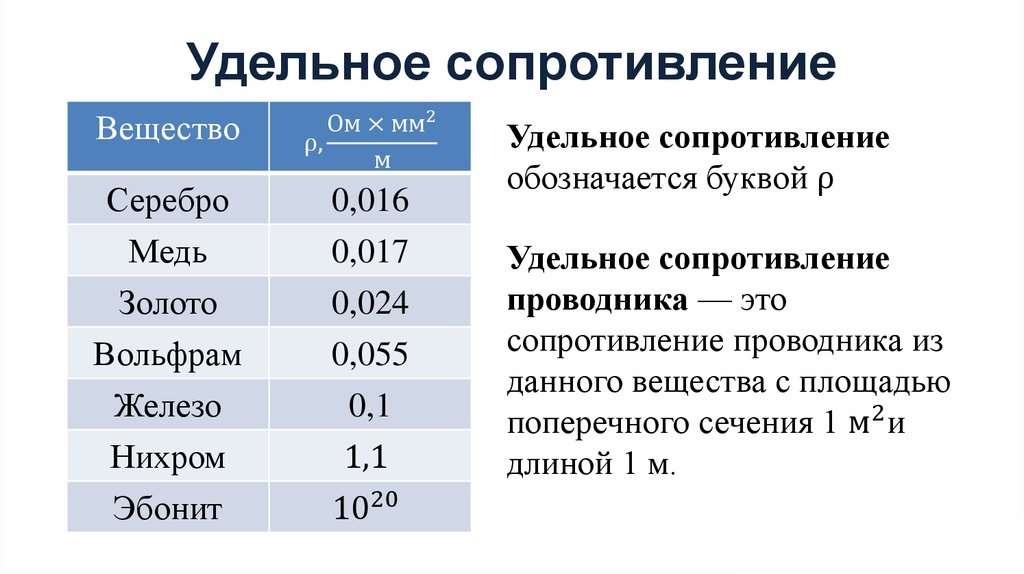
Удельное электрическое сопротивление
Дальнейшие исследования позволили установить связь величины электрического сопротивления с его основными геометрическими размерами. Оказалось, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника S.
Эта функциональная связь хорошо описывается следующей формулой:
$ R = ρ *{ L\over S} $ (4)
Постоянная для каждого вещества величина ρ была названа удельным сопротивлением. Значение этого параметра зависит от плотности вещества, его кристаллической структуры, строения атомов и прочих внутренних характеристик вещества. Из формулы (4) можно получить формулу для расчета удельного сопротивления, если имеются экспериментальные значения для R, L и S:
$ ρ = R*{ S\over L } $ (5)
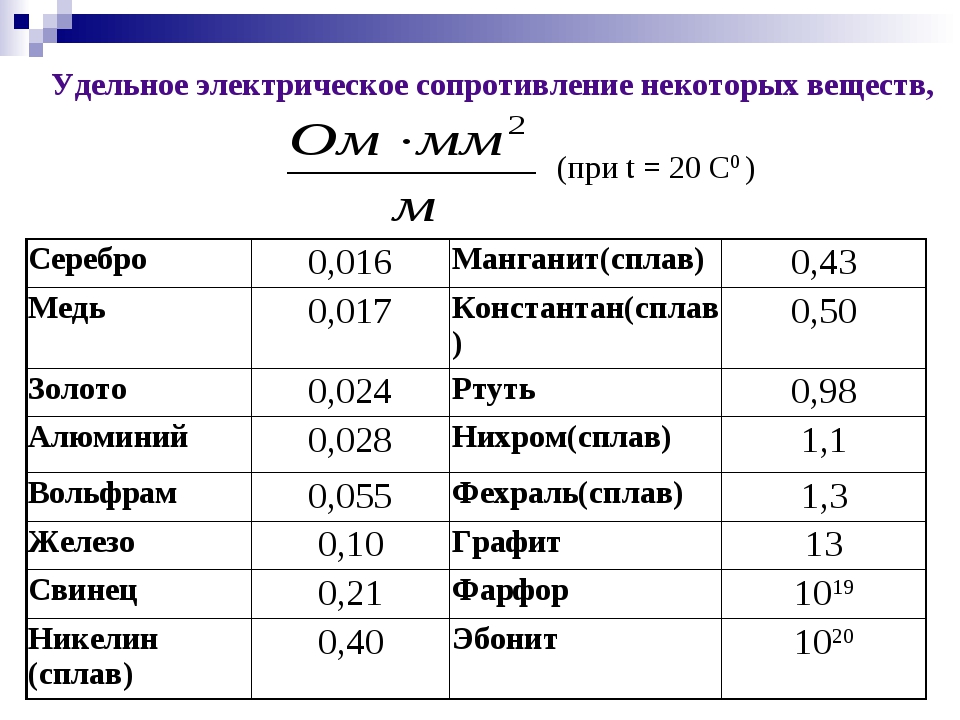
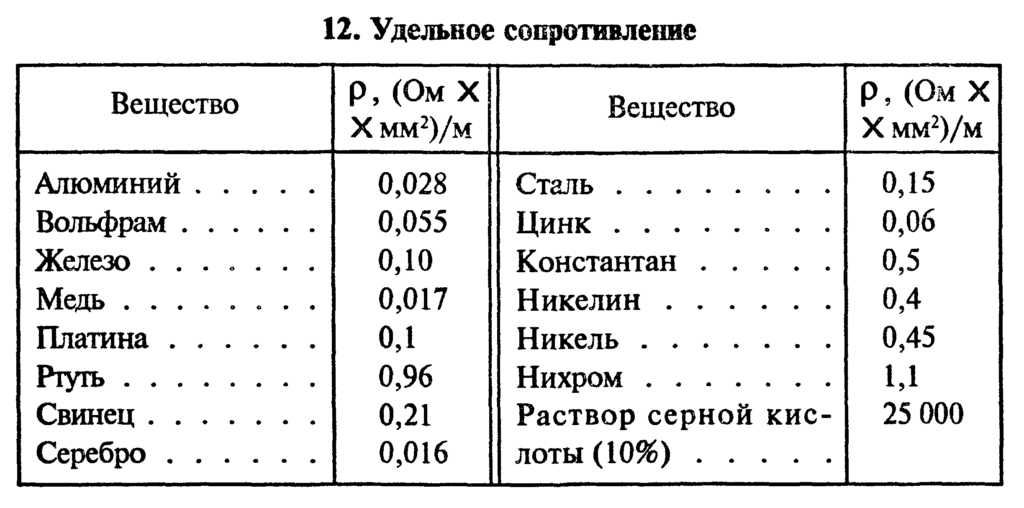
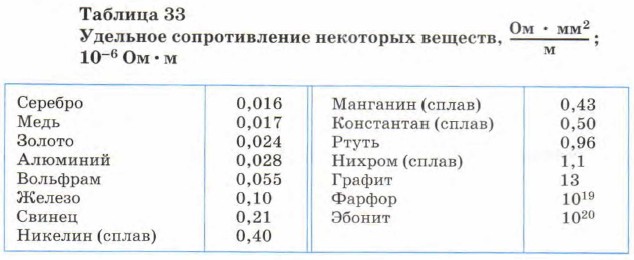
Для большинства известных веществ измерения были произведены и внесены в справочные таблицы электрических сопротивлений проводников.
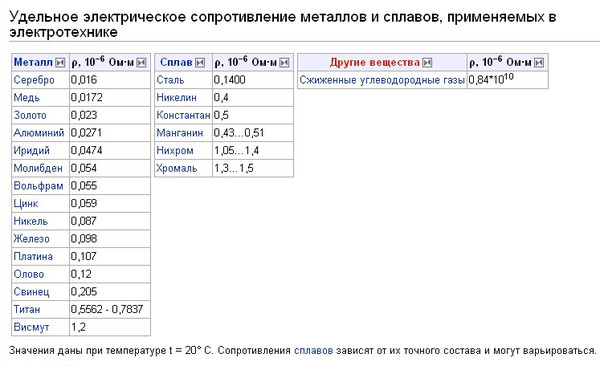
Удельное сопротивление металлов, Ом*мм2/м
(при Т = 20С)
|
Серебро |
0,016 |
Бронза (сплав) |
0,1 |
|
Медь |
0,017 |
Олово |
0,12 |
|
Золото |
0,024 |
Сталь (сплав) |
0,12 |
|
Алюминий |
0,028 |
Свинец |
0,21 |
|
Иридий |
0,047 |
Никелин (сплав) |
0,42 |
|
Молибден |
0,054 |
Манганин (сплав) |
0,45 |
|
Вольфрам |
0,055 |
Константан (сплав) |
0,48 |
|
Цинк |
0,06 |
Титан |
0,58 |
|
Латунь (сплав) |
0,071 |
Ртуть |
0,958 |
|
Никель |
0,087 |
Нихром (сплав) |
1,1 |
|
Платина |
0,1 |
Висмут |
1,2 |
Экспериментально было обнаружено, что с понижением температуры сопротивление металлов уменьшается. При приближении к температуре абсолютного нуля, которая равна -273С, сопротивление некоторых металлов стремится к нулю. Это явление называется сверхпроводимостью. Атомы и молекулы как бы “замораживаются”, прекращают любое движение и не оказывают сопротивления потоку электронов.
Что мы узнали?
Итак, мы узнали, что способность проводника ограничивать величину электрического тока называется сопротивлением. Величину сопротивления проводника можно определить с помощью закона Ома, измерив напряжение и ток. Если известно удельное сопротивление проводника, его длина и поперечное сечение, то сопротивление можно вычислить с помощью формулы (4), не измеряя ток и напряжение.
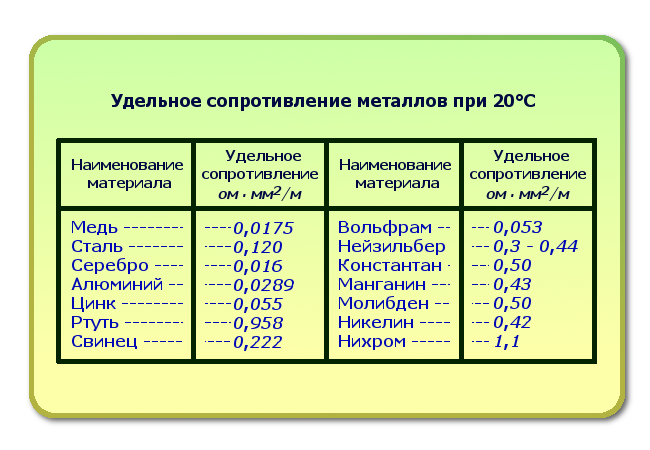
Таблица сопротивления металлов
Чтобы убедиться в преимуществах меди, надо сделать соответствующий сравнительный анализ. Ниже приведены значения сопротивлений металлов в сводной таблице.
Основные электрические параметры проводников, созданных из разных материалов
| Материал | Удельное сопротивление в Омах на метр, замеренное при комнатной температуре (+20°C) | Удельная электропроводность при аналогичных условиях, в сименсах на метр |
|---|---|---|
| Медь | 1,68х10^-3 | 5,96х10^7 |
| Серебро | 1,59х10^-3 | 6,3х10^7 |
| Золото | 2,44х10^-3 | 4,1х10^7 |
| Алюминий | 2,82х10^-3 | 3,5х10^7 |
| Вольфрам | 5,6х10^-3 | 1,79х10^7 |
| Железо | 1х10^-7 | 1х10^7 |
| Платина | 1,06х10^-7 | 9,43х10^6 |
| Литий | 9,28х10^-8 | 1,08х10^7 |
Важно! Малого сопротивления проводника из железа недостаточно для широкого применения соответствующих изделий на практике. Активное окисление провоцирует быстрое разрушение
Тонкие плёнки
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», RSq.{\displaystyle R_{\mathrm {Sq} }.} Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W: RSq=RWL,{\displaystyle R_{\mathrm {Sq} }=RW/L,} где R — измеренное сопротивление. В общем случае, если форма образца отличается от прямоугольной, и поле в плёнке неоднородное, используют метод ван дер Пау.