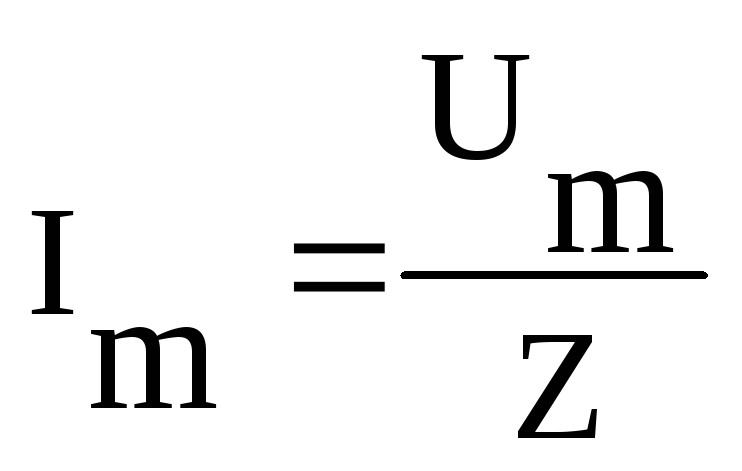Закон Ома для переменного тока

Закон Ома в дифференциальной форме

Сопротивление R{\displaystyle R} зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

J=σE,{\displaystyle \mathbf {J} =\sigma \mathbf {E} ,}

где:

• J{\displaystyle \mathbf {J} } — вектор плотности тока,
• σ{\displaystyle \sigma } — удельная проводимость,
• E{\displaystyle \mathbf {E} } — вектор напряжённости электрического поля.

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость σij{\displaystyle \sigma _{ij}} является симметричным тензором ранга (1, 1), а закон Ома, записанный в дифференциальной форме, приобретает вид

Ji=∑i=13σijEj.{\displaystyle J_{i}=\sum _{i=1}^{3}\sigma _{ij}E_{j}.}

Раздел физики, изучающий течение электрического тока (и другие электромагнитные явления) в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока[править]

Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига.

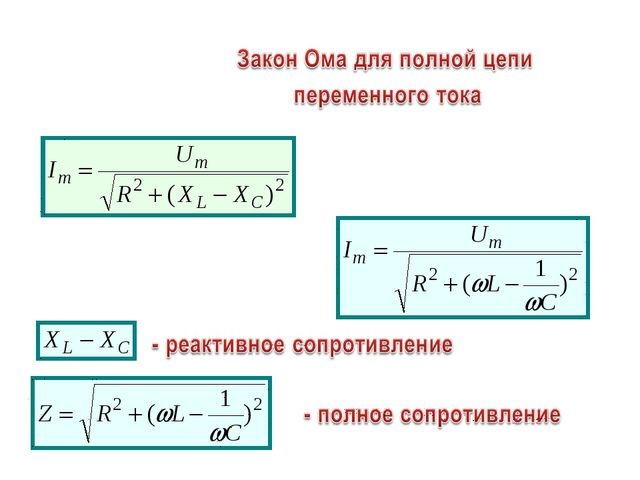
Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = Ueiωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re−iδ — комплексное сопротивление (электрический импеданс),
• R = √R_a2 + R_r2 — полное сопротивление,
• R_r = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ = − arctg (R_r/R_a) — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Трактовка и пределы применимости закона Ома[править]

Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций.

В классическом приближении закон Ома можно вывести при помощи теории Друде:

Здесь:

•  — электрическая удельная проводимость
•  — концентрация электронов
•  — элементарный заряд
•  — время релаксации по импульсам (время, за которое электрон «забывает» о том в какую сторону двигался)
•  — эффективная масса электрона

Проводники и элементы, для которых соблюдается закон Ома, называются омическими.

Закон Ома может не соблюдаться:

• При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
• При низких температурах для веществ, обладающих сверхпроводимостью.
• При заметном нагреве проводника проходящим током, в результате чего зависимость напряжения от тока (вольт-амперная характеристика) приобретает нелинейный характер. Классическим примером такого элемента является лампа накаливания.
• При приложении к проводнику или диэлектрику (например, воздуху или изоляционной оболочке) высокого напряжения, вследствие чего возникает пробой.
• В вакуумных и газонаполненных электронных лампах (в том числе люминесцентных).
• В гетерогенных полупроводниках и полупроводниковых приборах, имеющих p-n-переходы, например, в диодах и транзисторах.

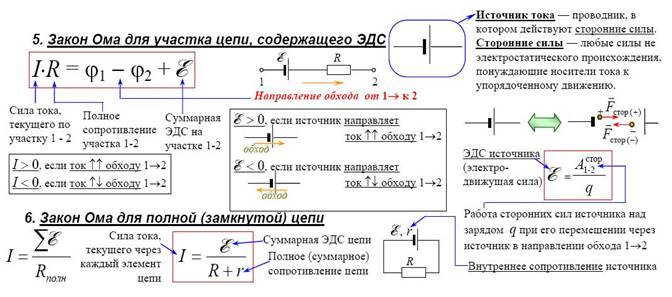
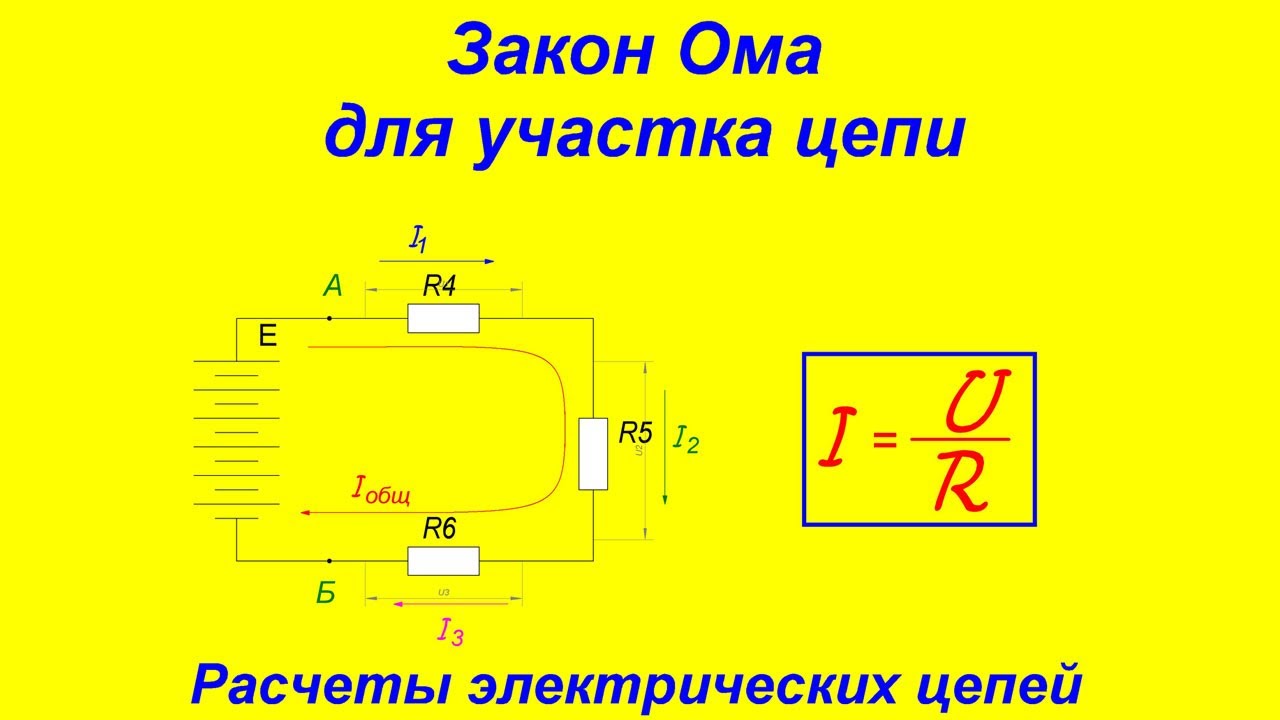
Закон Ома для неоднородного участка цепи

Физическая величина, равная отношению работы сторонних сил A_ст при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой (ЭДС) источника E_эдс:

$ E_{эдс} = {A_{cт}\over q} $ (1).

Таким образом, ЭДС равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда. При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа электростатического поля равна нулю, а работа сторонних сил равна сумме всех ЭДС, действующих в этой цепи.

Работа электростатических сил по перемещению единичного заряда равна разности потенциалов $ Δφ = φ_1 – φ_2 $ между начальной и конечной точками 1 и 2 неоднородного участка. Работа сторонних сил равна, по определению, электродвижущей силе E_эдс, действующей на данном участке. Поэтому полная работа равна:

$ U_п = φ_1 – φ_2 + E_{эдc} $ (2).

Величина U_п называется напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:

$ U_п = φ_1 – φ_2 $ (3).

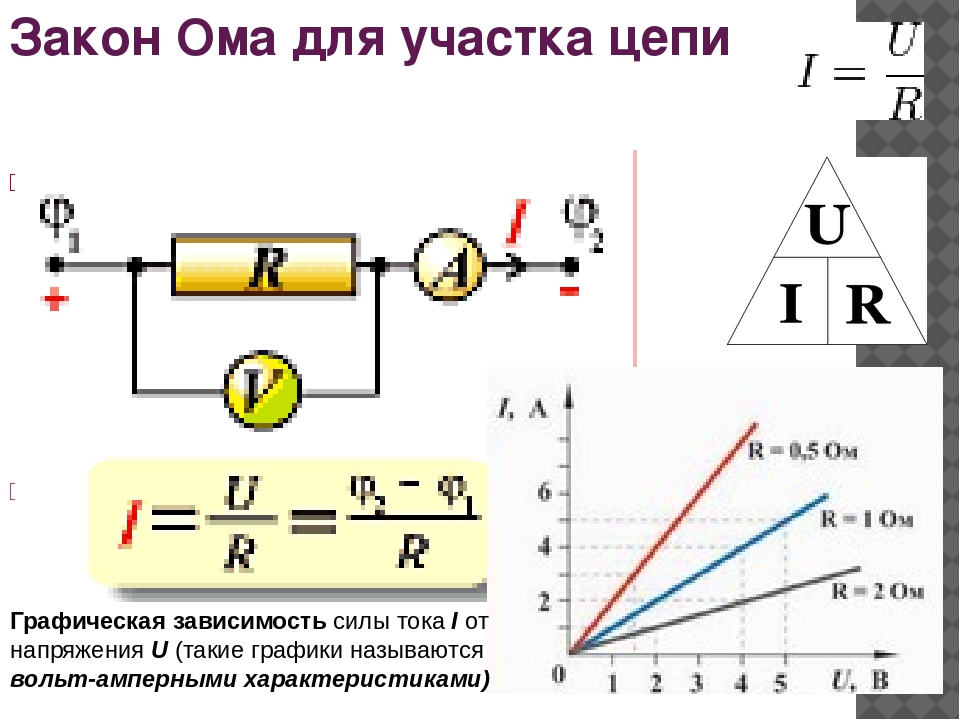
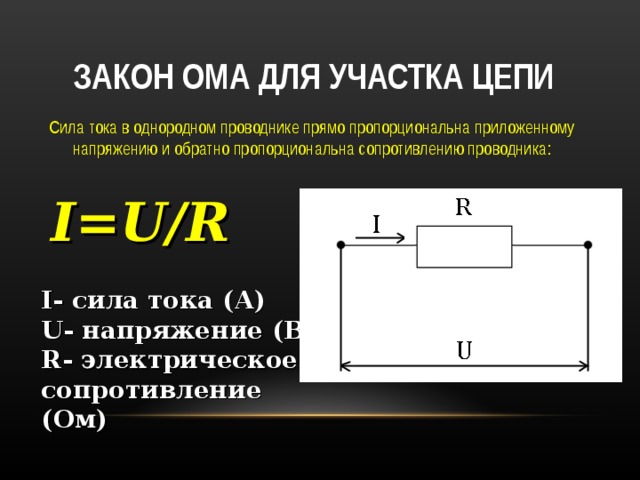
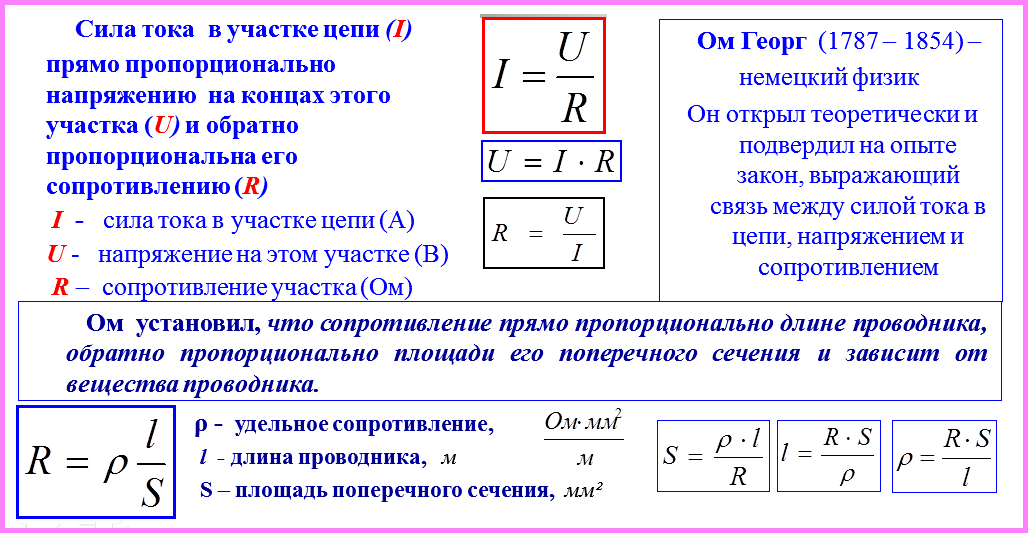
Немецкий исследователь Георг Симон Ом в начале XIX века установил, что сила тока I, текущего по однородному проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

$ I = {U \over R} $ (4).

Рис. 2. Портрет Георга Ома.

Величина R — это электрическое сопротивление. Уравнение (4) выражает закон Ома для однородного участка цепи. Для участка цепи, содержащего ЭДС, закон Ома записывается в следующем виде:

$ U_п = I * R = φ_1 – φ_2 + E_{эдс} = Δ φ_{12} + E_{эдс}$ (5).

Данное уравнение называется обобщенным законом Ома для неоднородного участка цепи.

Формула

Закон Ома не может быть применен к цепям переменного потока электронов, поскольку он не учитывает реактивное сопротивление, которое всегда присутствует в таких цепях. Однако, изменяя закон Ома, который учитывает влияние реактивного сопротивления, получается общий закон Ома для последовательной цепи переменного тока, применимый к цепям этого движения (закон Ома для постоянного и переменного тока). Поскольку полное сопротивление Z представляет собой совокупное сопротивление всех реактивных сопротивлений, то общий закон Ома для переменного тока: I=E/Z

Эта общая модификация применяется к переменному потоку электронов, протекающему в любой цепи, и любое из значений может быть найдено из уравнения, если другие известны.

Применение закона

Если технические специалисты во время тестирования стандартных показателей разрядов обнаружат, что обычные значения не регистрируются на их цифровых мультиметрах или измерителях токовых клещей, то они могут использовать закон Ома, чтобы определить, какая часть цепи дает сбой, и исходя из этого определить, в чем может заключаться проблема.

Мнемоническая диаграмма для Закона[править]

Схема, иллюстрирующая три составляющие закона Ома

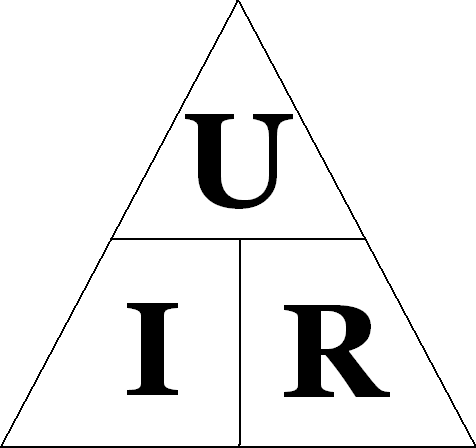
Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

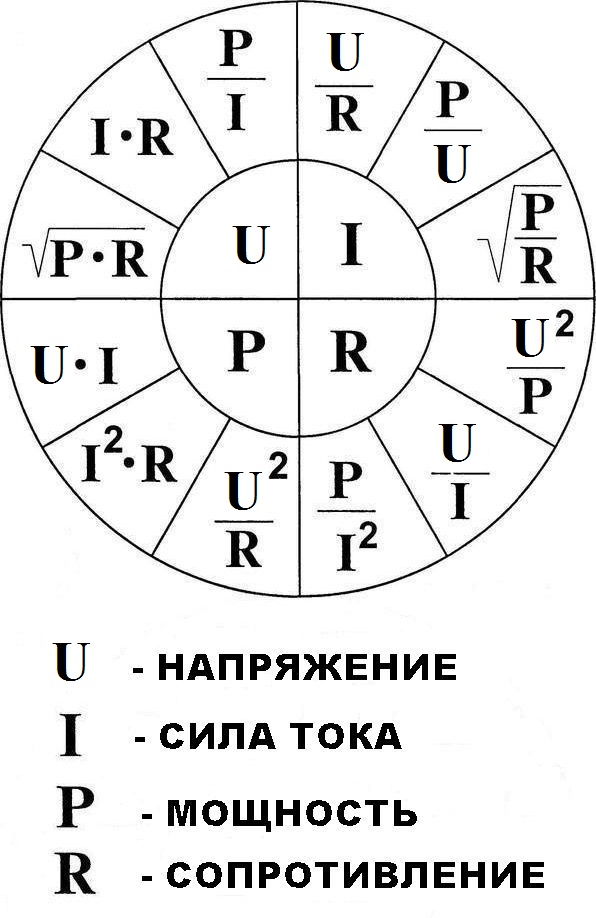
Электрическое напряжениеСила токаЭлектрическая мощностьЭлектрическое сопротивление

В соответствии с этой диаграммой формально может быть записано выражение:

которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

где:

•  — удельное электрическое сопротивление материала, из которого сделан проводник,
•  — его длина
•  — площадь его поперечного сечения

Закон Ома и ЛЭПправить

Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи = , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением:

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

Основные понятия

Электрический ток течёт, когда замкнутый контур позволяет электронам перемещаться от высокого потенциала к более низкому в цепи. Иначе говоря, ток требует источника электронов, обладающего энергией для приведения их в движение, а также точки их возвращения отрицательных зарядов, для которой характерен их дефицит. Как физическое явление ток в цепи характеризуется тремя фундаментальными величинами:

• напряжение;
• сила тока;
• сопротивление проводника, по которому движутся электроны.

Сила и напряжение

Сила тока (I, измеряется в Амперах) есть объём электронов (заряд), перемещающихся через место в цепи за единицу времени. Иными словами, измерение I — это определение количества электронов, находящихся в движении

Важно понимать, что термин относится только к движению: статические заряды, например, на клеммах неподсоединённой батареи, не имеют измеряемого значения I. Ток, который протекает в одном направлении, называется постоянным (DC), а периодически изменяющий направление — переменным (AC)

Напряжение можно проиллюстрировать таким явлением, как давление, или как разность потенциальной энергии предметов под воздействием гравитации. Для того чтобы создать этот дисбаланс, нужно затратить предварительно энергию, которая и будет реализована в движении при соответствующих обстоятельствах. Например, в падении груза с высоты реализуется работа по его подъёму, в гальванических батареях разность потенциалов на клеммах образуется за счёт преобразования химической энергии, в генераторах — в результате воздействия электромагнитного поля.

Сопротивление проводников

Независимо от того, насколько хорош обычный проводник, он никогда не будет пропускать сквозь себя электроны без какого-либо сопротивления их движению. Можно рассматривать сопротивление как аналог механического трения, хотя это сравнение не будет совершенным. Когда ток протекает через проводник, некоторая разность потенциалов преобразуется в тепло, поэтому всегда будет падение напряжения на резисторе. Электрические обогреватели, фены и другие подобные устройства предназначены исключительно для рассеивания электрической энергии в виде тепла.

Упрощённо сопротивление (обозначается как R) является мерой того, насколько поток электронов тормозится в цепи. Оно измеряется в Омах. Проводимость резистора или другого элемента определяется двумя свойствами:

• геометрией;
• материалом.

Форма имеет важнейшее значение, это очевидно на гидравлической аналогии: протолкнуть воду через длинную и узкую трубу гораздо тяжелее, чем через короткую и широкую. Материалы играют определяющую роль. Например, электроны могут свободно перемещаться в медном проводе, но не способны протекать вообще через такие изоляторы, как каучук, независимо от их формы. Кроме геометрии и материала, существуют и другие факторы, влияющие на проводимость.

Трактовка и пределы применимости закона Ома

Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций.

В классическом приближении закон Ома можно вывести при помощи теории Друде:

J=n⋅e2⋅τm⋅E=σ⋅E.{\displaystyle \mathbf {J} ={\frac {n\cdot e_{0}^{2}\cdot \tau }{m}}\cdot \mathbf {E} =\sigma \cdot \mathbf {E} .}

Здесь:

• σ{\displaystyle \sigma } — электрическая удельная проводимость;
• n{\displaystyle n} — концентрация электронов;
• e{\displaystyle e_{0}} — элементарный заряд;
• τ{\displaystyle \tau } — время релаксации по импульсам (время, за которое электрон «забывает» о том, в какую сторону двигался);
• m{\displaystyle m} — эффективная масса электрона.

Проводники и элементы, для которых соблюдается закон Ома, называются омическими.

Закон Ома может не соблюдаться:

• При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
• При низких температурах для веществ, обладающих сверхпроводимостью.
• При заметном нагреве проводника проходящим током, в результате чего зависимость напряжения от тока (вольт-амперная характеристика) приобретает нелинейный характер. Классическим примером такого элемента является лампа накаливания.
• При приложении к проводнику или диэлектрику (например, воздуху или изоляционной оболочке) высокого напряжения, вследствие чего возникает пробой.
• В вакуумных и газонаполненных электронных лампах (в том числе люминесцентных).
• В гетерогенных полупроводниках и полупроводниковых приборах, имеющих p-n-переходы, например, в диодах и транзисторах.

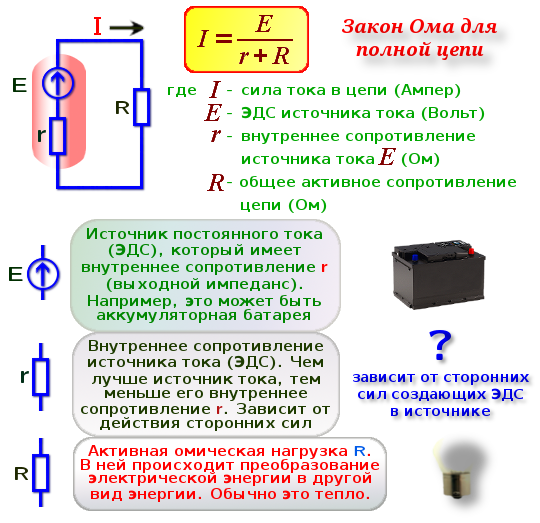
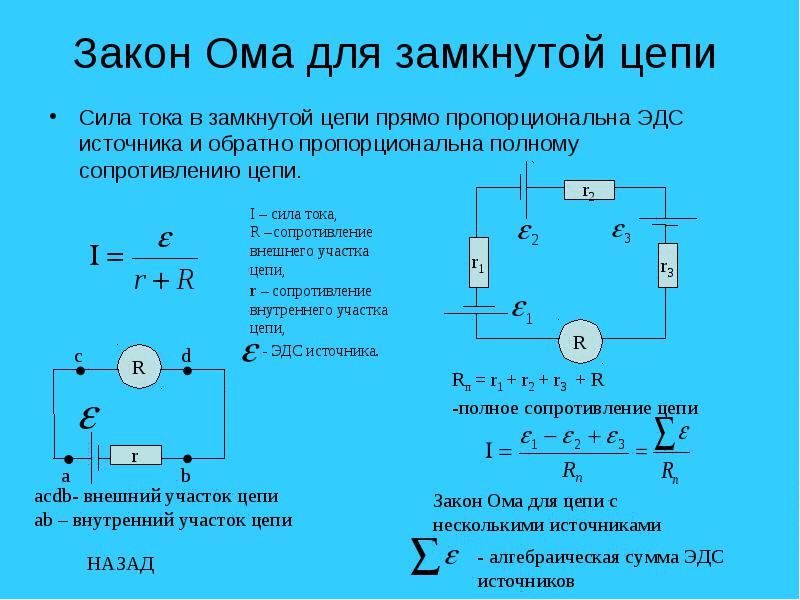
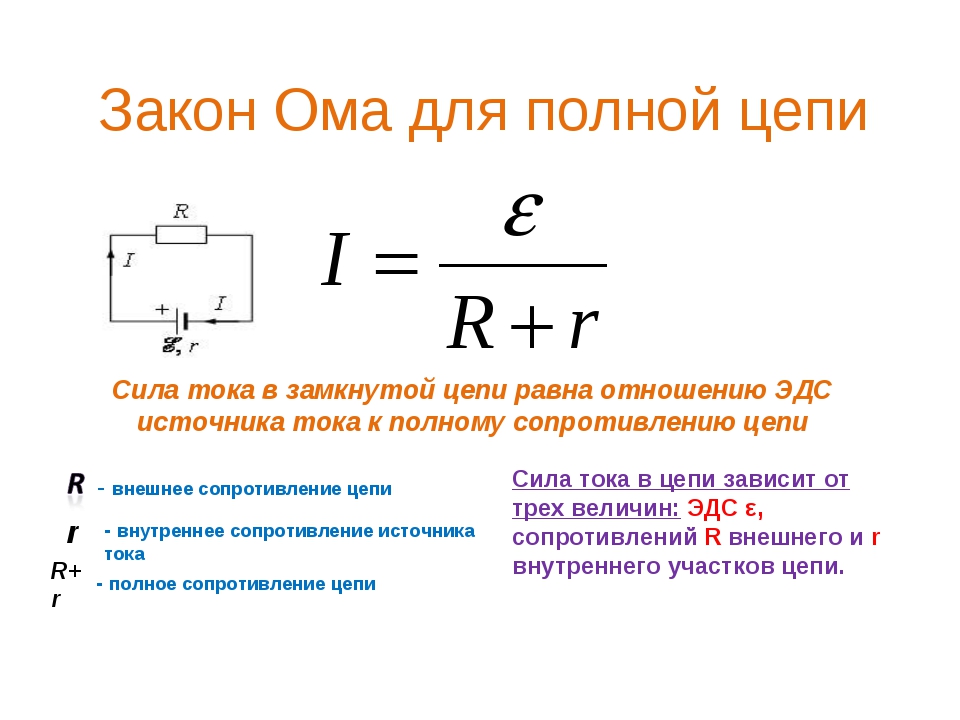
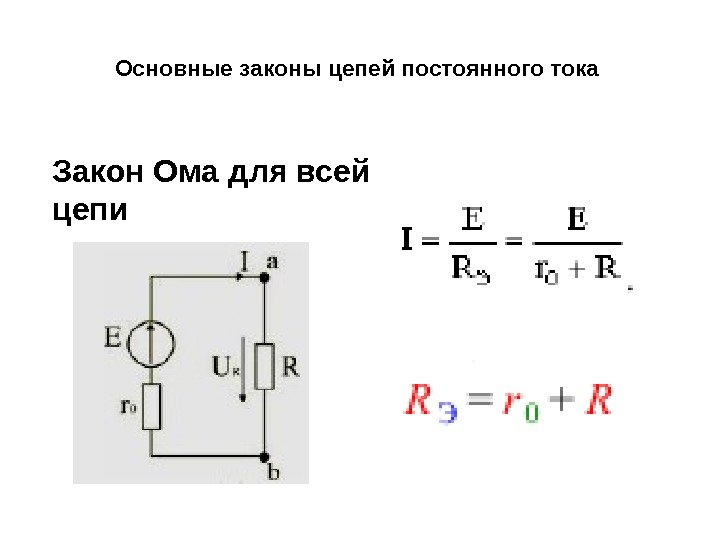
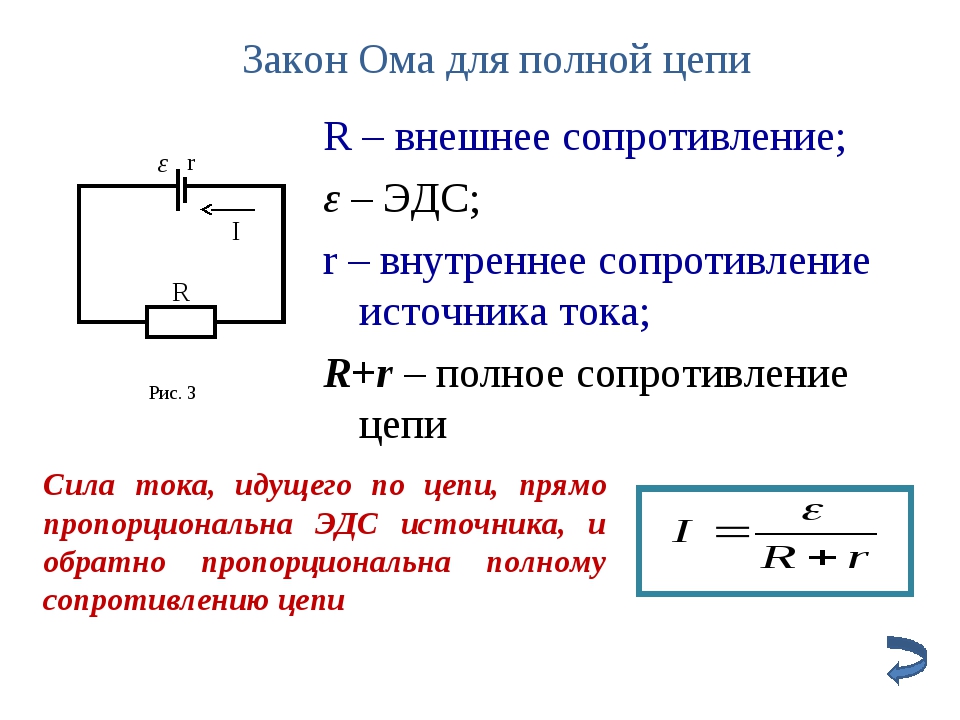
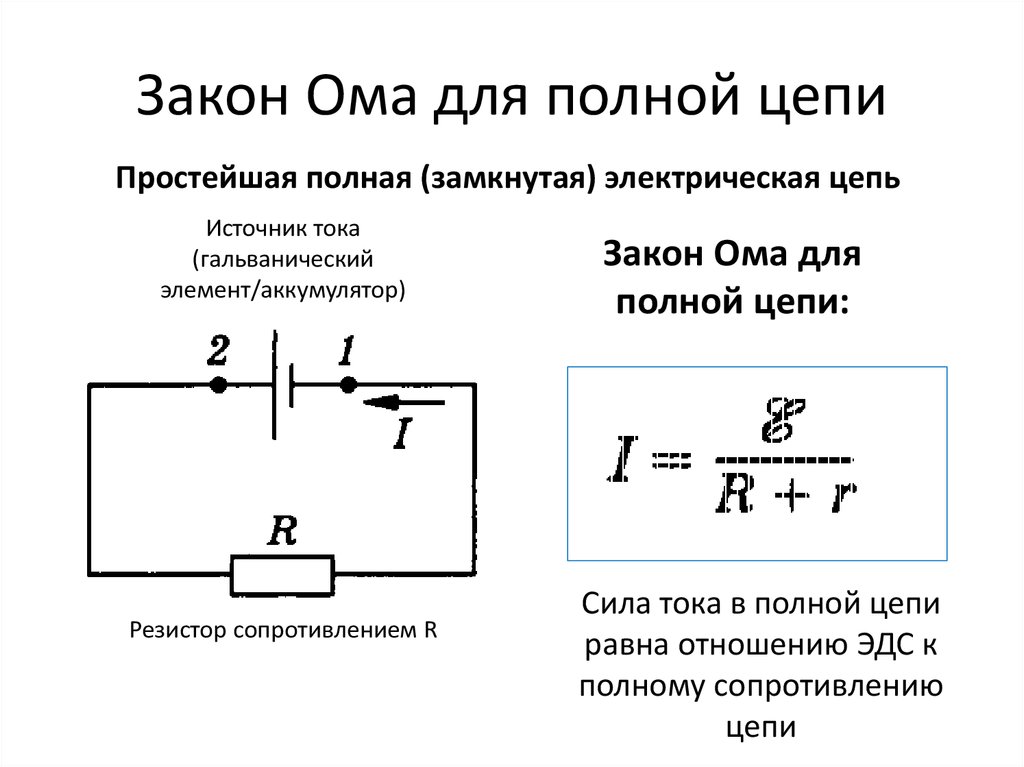
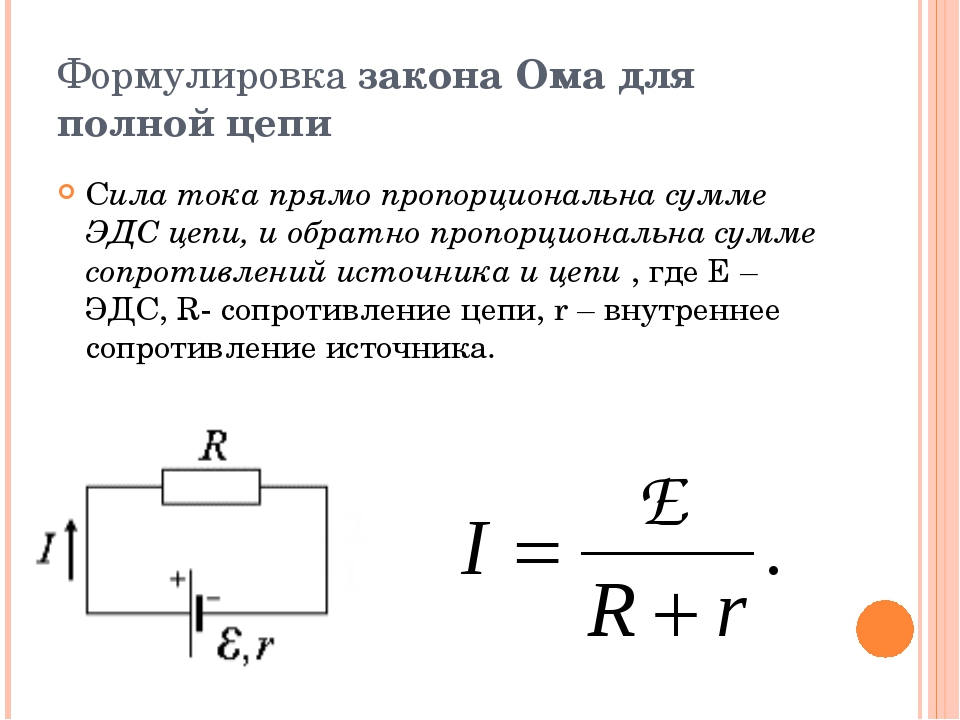
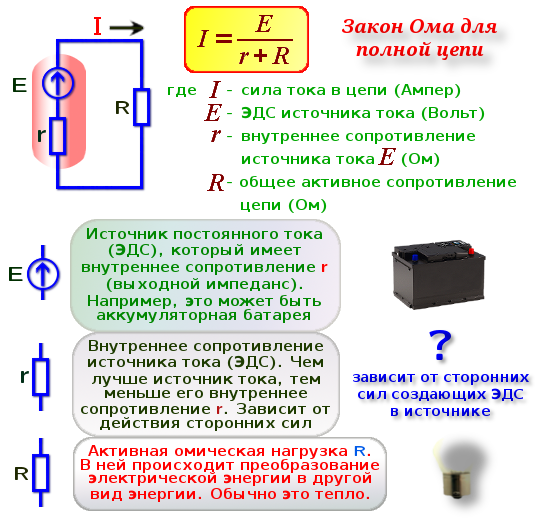
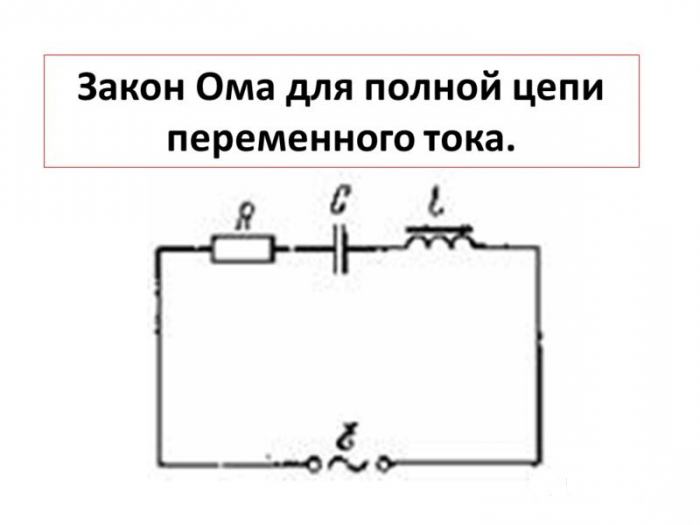
Закон ома для полной цепи

Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.

Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.

Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта. Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания. Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.

Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока. По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами. Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет разность потенциалов.

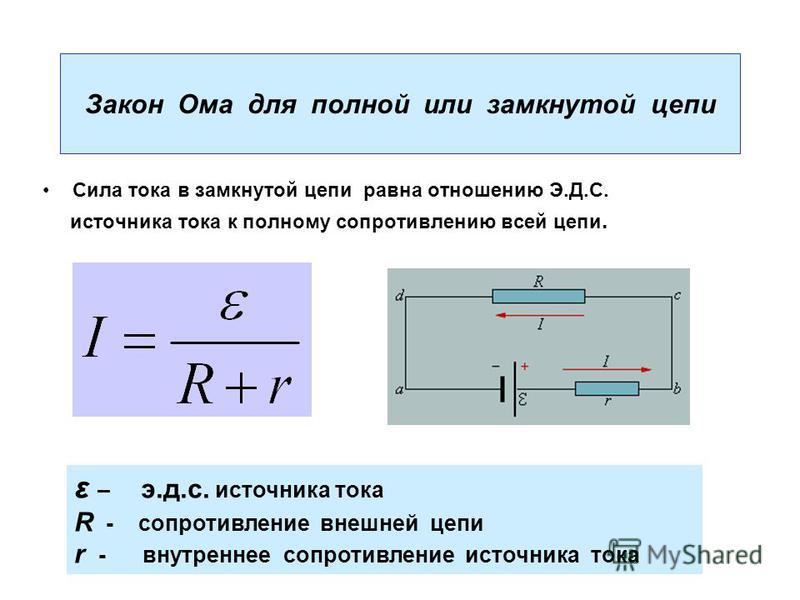
Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела. Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r). На размеры силы тока влияет такое понятие, как электродвижущая сила – ЭДС, прилагаемая к электродам, обозначенная символом Е.

Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U

ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока. В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы. Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода.

Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка.

Трактовка и пределы применимости закона Ома

Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций.

В классическом приближении закон Ома можно вывести при помощи теории Друде:

J=n⋅e2⋅τm⋅E=σ⋅E.{\displaystyle \mathbf {J} ={\frac {n\cdot e_{0}^{2}\cdot \tau }{m}}\cdot \mathbf {E} =\sigma \cdot \mathbf {E} .}

Здесь:

• σ{\displaystyle \sigma } — электрическая удельная проводимость;
• n{\displaystyle n} — концентрация электронов;
• e{\displaystyle e_{0}} — элементарный заряд;
• τ{\displaystyle \tau } — время релаксации по импульсам (время, за которое электрон «забывает» о том, в какую сторону двигался);
• m{\displaystyle m} — эффективная масса электрона.

Проводники и элементы, для которых соблюдается закон Ома, называются омическими.

Закон Ома может не соблюдаться:

• При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
• При низких температурах для веществ, обладающих сверхпроводимостью.
• При заметном нагреве проводника проходящим током, в результате чего зависимость напряжения от тока (вольт-амперная характеристика) приобретает нелинейный характер. Классическим примером такого элемента является лампа накаливания.
• При приложении к проводнику или диэлектрику (например, воздуху или изоляционной оболочке) высокого напряжения, вследствие чего возникает пробой.
• В вакуумных и газонаполненных электронных лампах (в том числе люминесцентных).
• В гетерогенных полупроводниках и полупроводниковых приборах, имеющих p-n-переходы, например, в диодах и транзисторах.

Формула

Основную формулу закона Ома можно представить в математическом варианте. При помощи закона Ома вполне возможно определить, какие изменения произойдут с силой тока на определенном участке цепи, при изменениях напряжения и сопротивления на этом же участке:

• Согласно приведенной формуле, при увеличении напряжения на концах участка электрической цепи, сила тока на этом участке также будет возрастать. Во сколько раз может уменьшиться или увеличиться напряжение, во столько же уменьшается или увеличивается сила тока. Такие изменения возможны при условии постоянного сопротивления.
• В том случае, когда напряжение остается неизменным, сила тока переходит в зависимость от значения сопротивления. То есть, при возрастании сопротивления на каком-либо определенном участке цепи начинает пропорционально уменьшаться. Если сопротивление уменьшается, то сила тока, соответственно, возрастает.

В случае превышения допустимого значения для конкретного участка цепи все приборы, включенные в эту цепь, могут выйти из строя. При этом, провода раскаляются, вплоть до возгорания. Данная ситуация является классической при возникновении короткого замыкания, когда две точки цепи, находящиеся под напряжением, соединяются проводником, имеющим очень небольшое сопротивление.

Формула закона Ома позволяет избежать подобных ситуаций, предполагая предварительное определение сопротивления для того или иного участка электрической цепи. Для того, чтобы определить это значение, необходимо измерить на данном участке сначала напряжение, а, затем силу тока. После этого, первую величину необходимо разделить на вторую. Полученный результат и будет тем значением сопротивления.

При определении напряжения на концах цепи, нужно значение силы тока умножить на значение напряжения.

Закон Джоуля-Ленца

Закон электромагнитной индукции формула

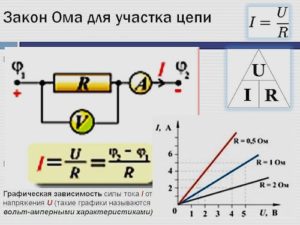
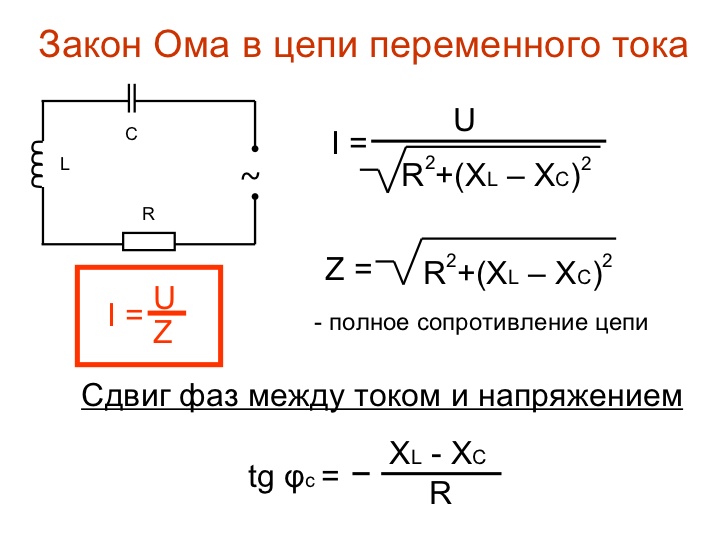
Закон Ома для переменного тока

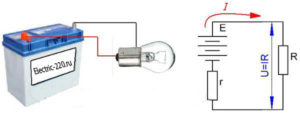
Закон Ома для полной цепи

Калькулятор для расчета Закона Ома

Закон Фарадея для электролиза

Для переменного тока

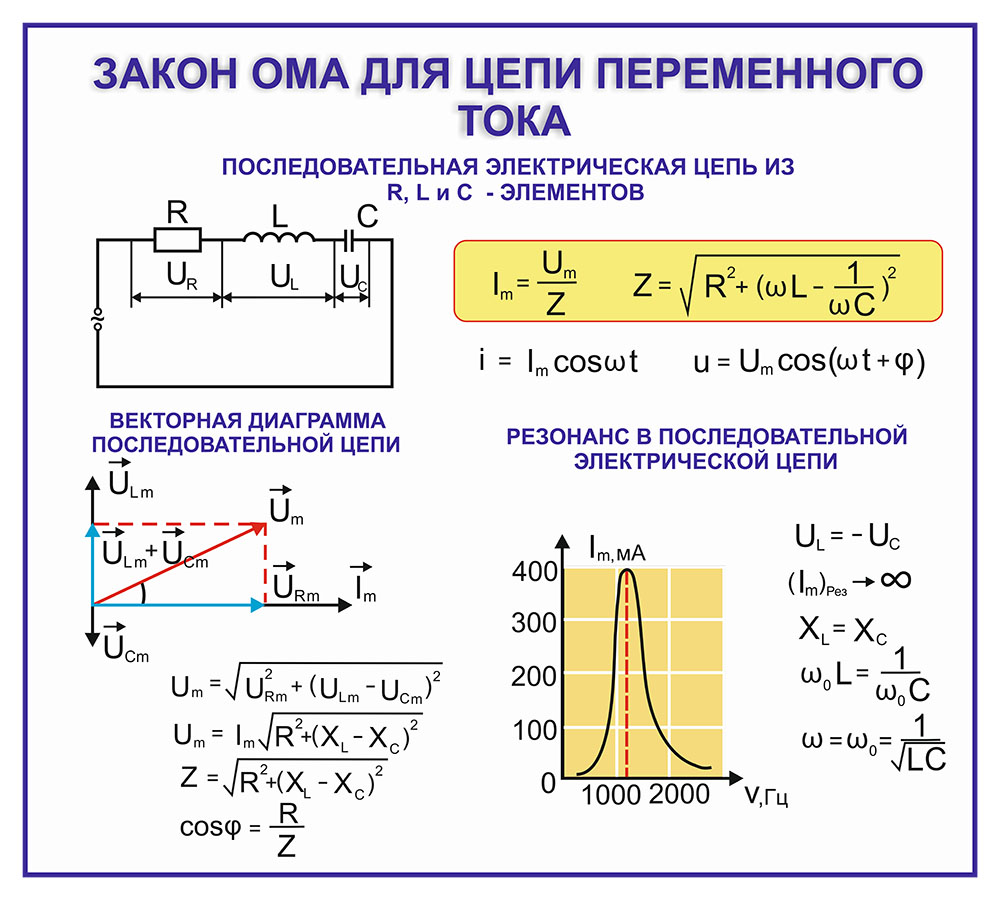
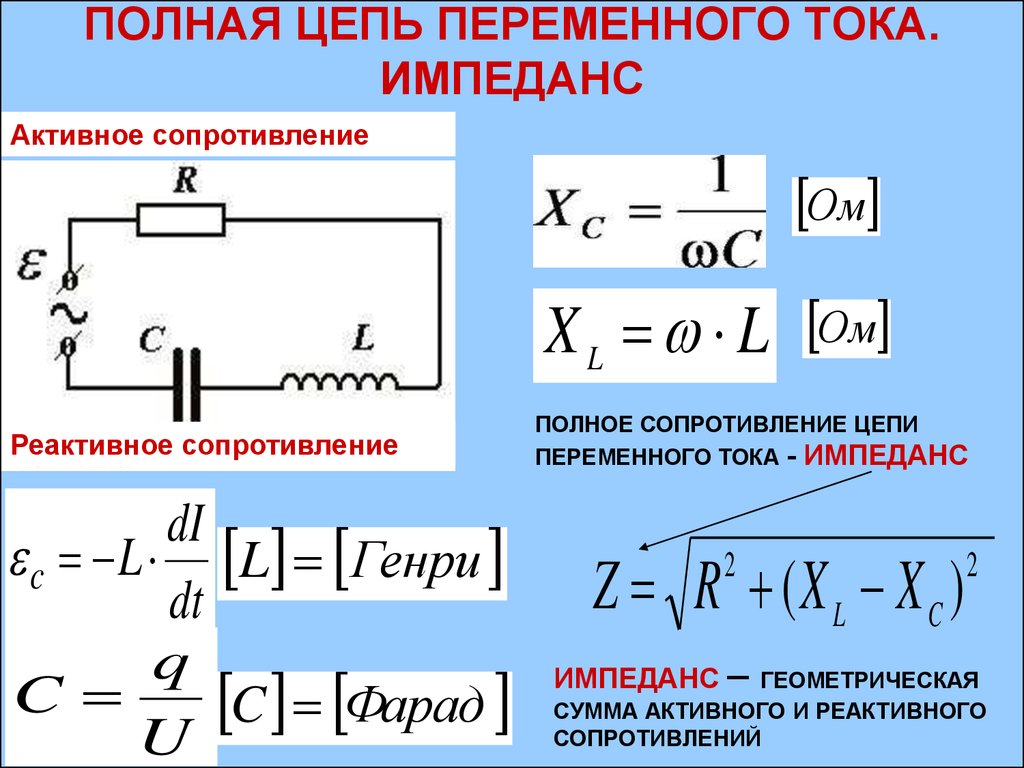
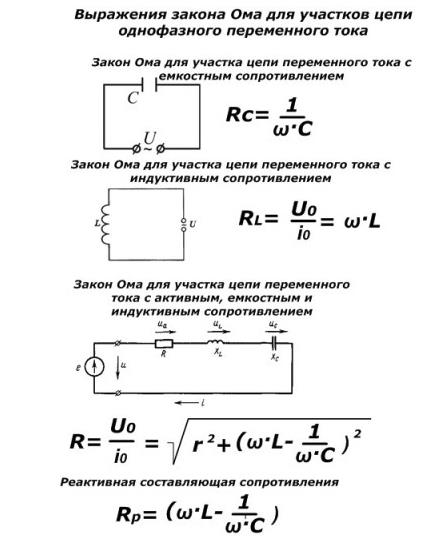
Нужно понимать, что закон не применим напрямую к переменным цепям, например, с катушками индуктивности, конденсаторами или линиям передач. Закон может использоваться только для чисто резистивных цепей переменного тока без каких-либо изменений. В цепи RLC противодействие току является импедансом Z, который образует комбинацию двух ортогональных частей сопротивления.

Переменный ток

Im=Vm/Z

В этом случае Vm связано с Im с помощью константы пропорциональности Z (импеданса) и константы пропорциональности R. Для чисто резистивных линий, где (Z = R).

Vm = ImZ и Vm = ImR

Z — это общее сопротивление участка к переменному току, состоящее из реальной части — сопротивления и мнимой — реактивности.

Формула ее определяется теоремой Пифагора, поскольку угол Ф зависит от реактивной составляющей.

Интегральная форма

Мнемоническая диаграмма для Закона[править]

Схема, иллюстрирующая три составляющие закона Ома

Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

Электрическое напряжениеСила токаЭлектрическая мощностьЭлектрическое сопротивление

В соответствии с этой диаграммой формально может быть записано выражение:

которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

где:

•  — удельное электрическое сопротивление материала, из которого сделан проводник,
•  — его длина
•  — площадь его поперечного сечения

Закон Ома и ЛЭПправить

Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи = , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением:

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

Закон Ома для переменного тока

Если в электроцепи имеется емкость или инертность, то этот факт следует однозначно учитывать при расчётах силы тока. Они имеют собственные показатели сопротивления, что приводит к ситуации, которая будет иметь переменный характер. В случае Закона Ома для переменного тока формула записывается следующим образом:

I = U/ Z, где

I – сила тока, U – напряжение, а Z – суммарное значение сопротивления на всех участках электрической цепи (этот параметр именуется еще, как импеданс).

Как говорилось изначально, закон Ома считается эмпирическим. Это обозначает то, что он может не всегда работать и выполнять вычисления на его основе не представляется возможным. Подобная ситуация может сложиться в нескольких случаях:

• в ситуации, когда электросеть имеет высокую частоту и электромагнитное поле может сильно изменяться за короткие промежутки времени;
• при наличии проводников, которые обладают свойствами сверхпроводимости, расположенных в условиях низких температурных показателей;
• при перегреве проводника под воздействием проходящего по нему тока, отношение напряжения и сопротивления может носить переменный, неоднородный характер;
• если проводник (диэлектрик) находится под высоким напряжением;
• светодиодных лампах;
• в полупроводниках и аналогичных устройствах.

На основе этого закона, можно произвести вывод некоторых формул математическим путем. С их помощью можно производить разнообразные расчеты.

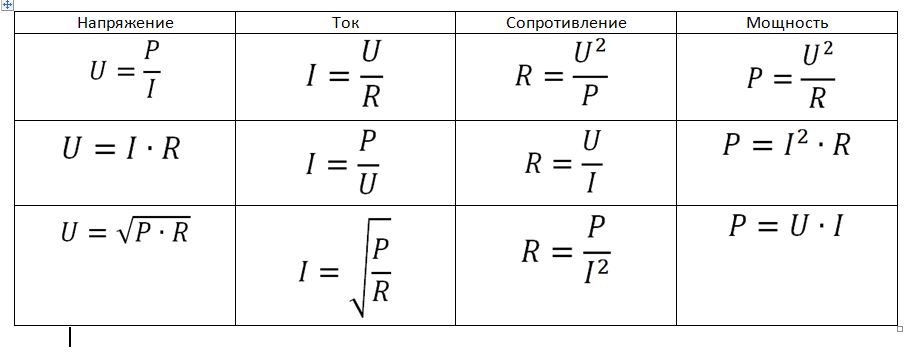
Мнемоническая диаграмма для закона Ома

Схема, иллюстрирующая три составляющие закона Ома

Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

U — электрическое напряжение;I — сила тока;P — электрическая мощность;R — электрическое сопротивление

В соответствии с этой диаграммой формально может быть записано выражение:

R=UI,(7){\displaystyle R\!={U \over I},\qquad (7)}

которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

R=ϱls,(8){\displaystyle R\!={\varrho l \over s},\qquad (8)}

где:

• ϱ{\displaystyle \varrho } — удельное электрическое сопротивление материала, из которого сделан проводник,
• l{\displaystyle l} — его длина
• s{\displaystyle s} — площадь его поперечного сечения

Закон Ома и ЛЭП

Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами, задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока P{\displaystyle P} = εI{\displaystyle {\varepsilon \!I\!}} при минимальных потерях мощности в линии передачи P(r)=UI,{\displaystyle P(r)=UI,} где U=Ir,{\displaystyle U\!=Ir,} причём r{\displaystyle r} на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением

P(r)=P2rε2.(9){\displaystyle P(r)={\frac {P^{2}r}{\varepsilon ^{2}}}.\qquad (9)}

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное увеличение ЭДС. Однако ЭДС ограничивается электрической прочностью обмотки генератора, поэтому повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в линии возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.