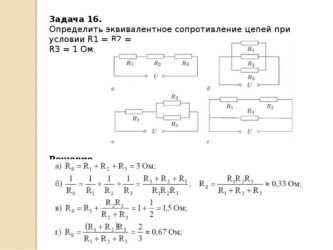
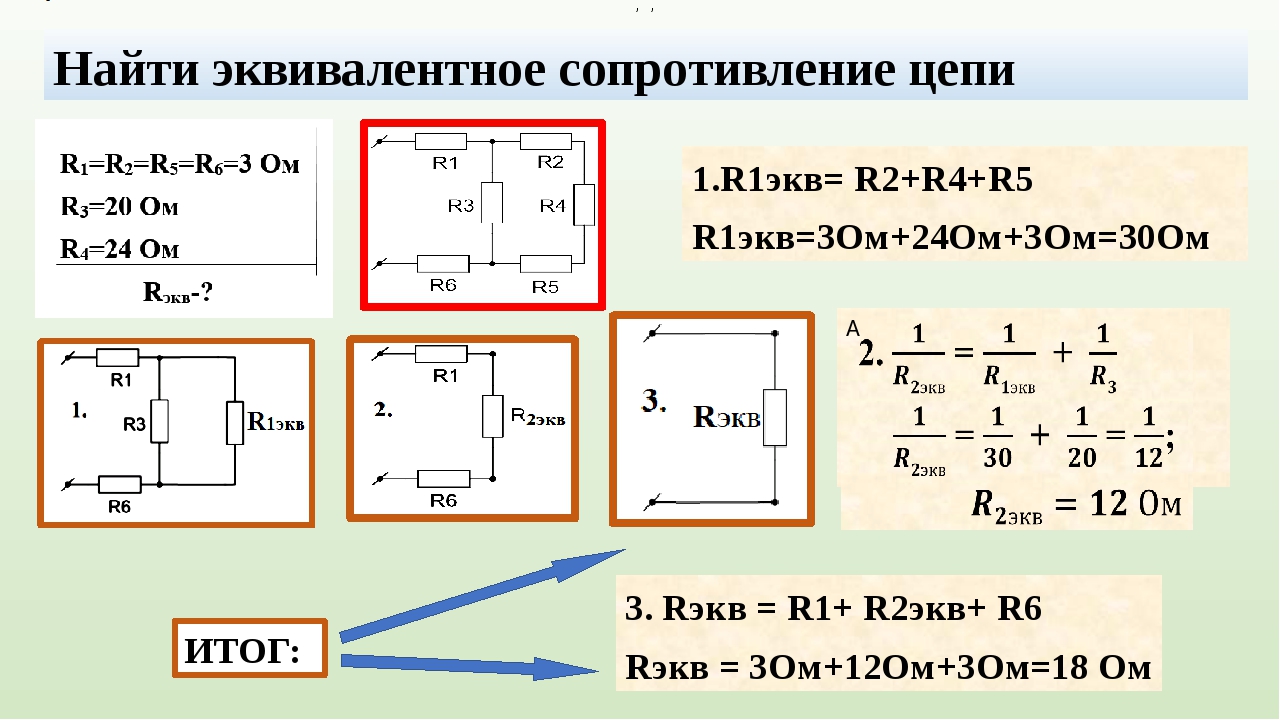
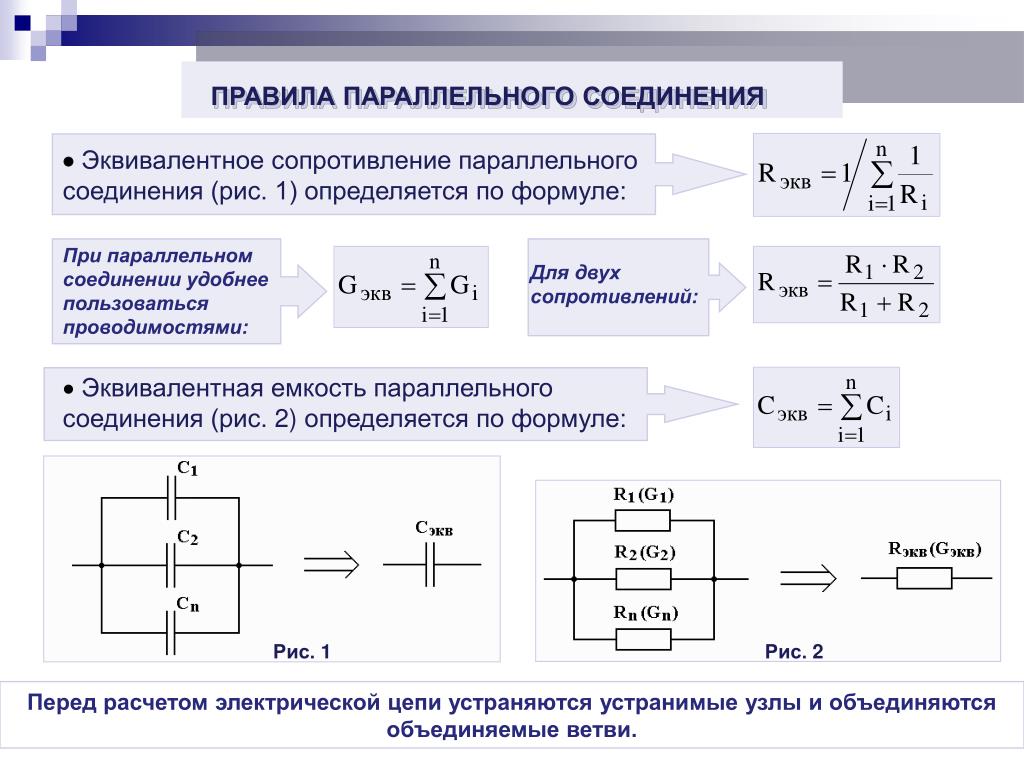
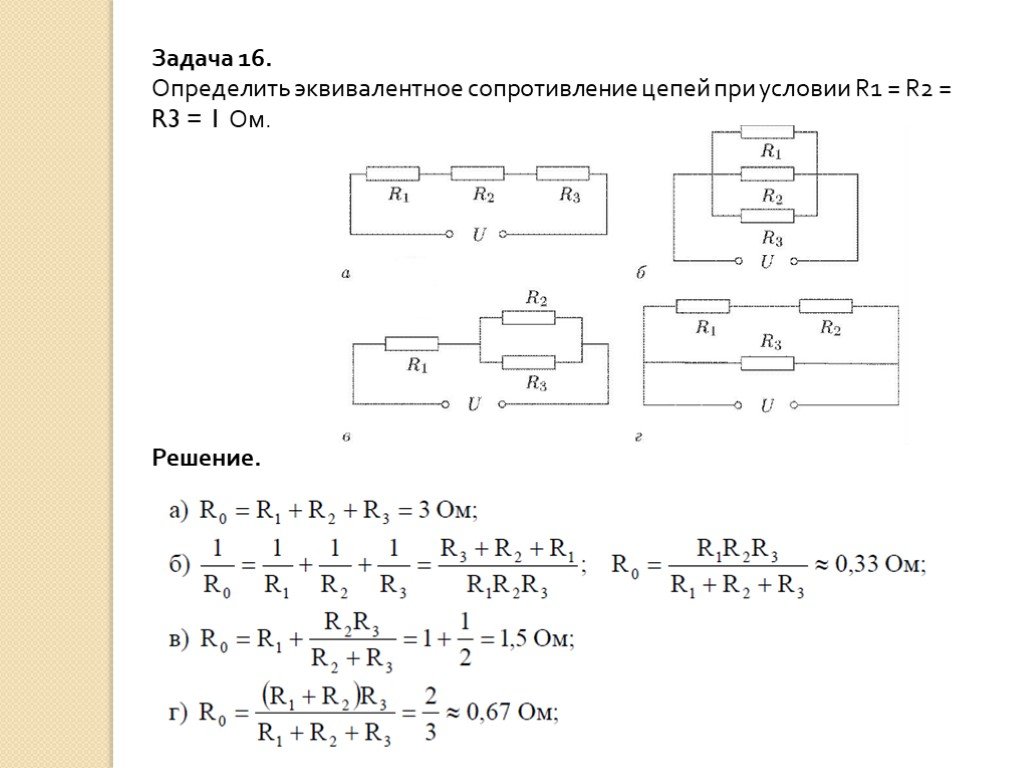
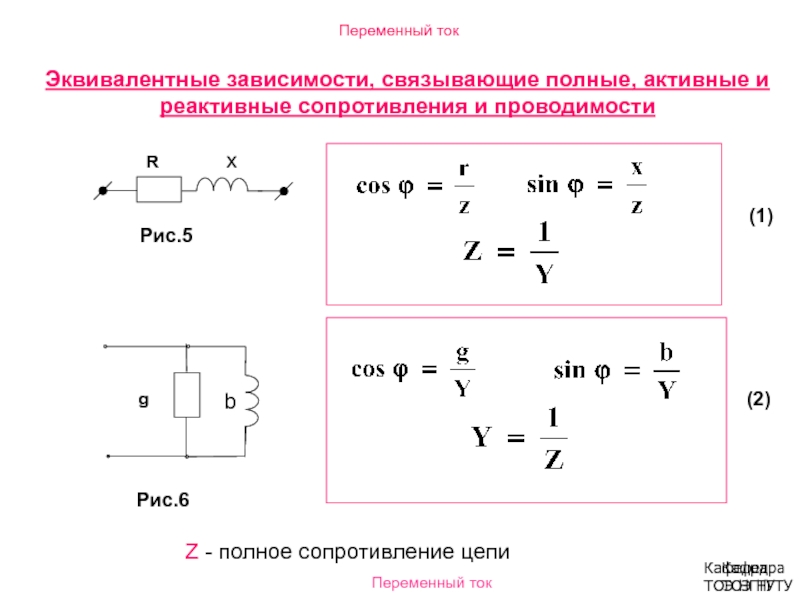
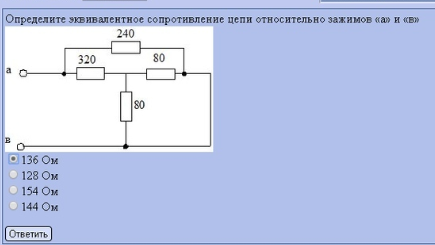
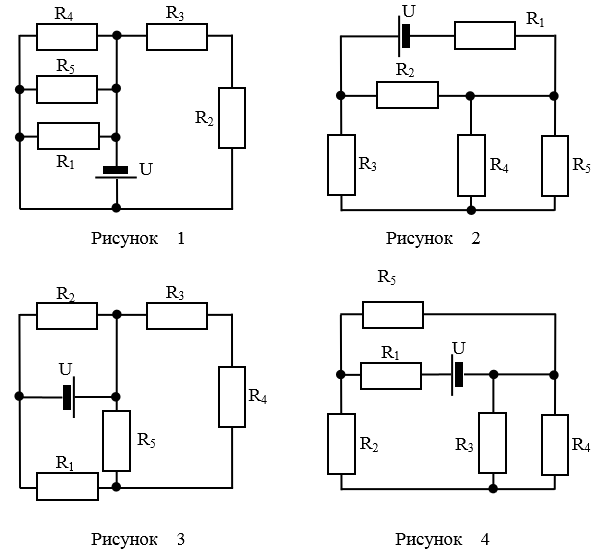
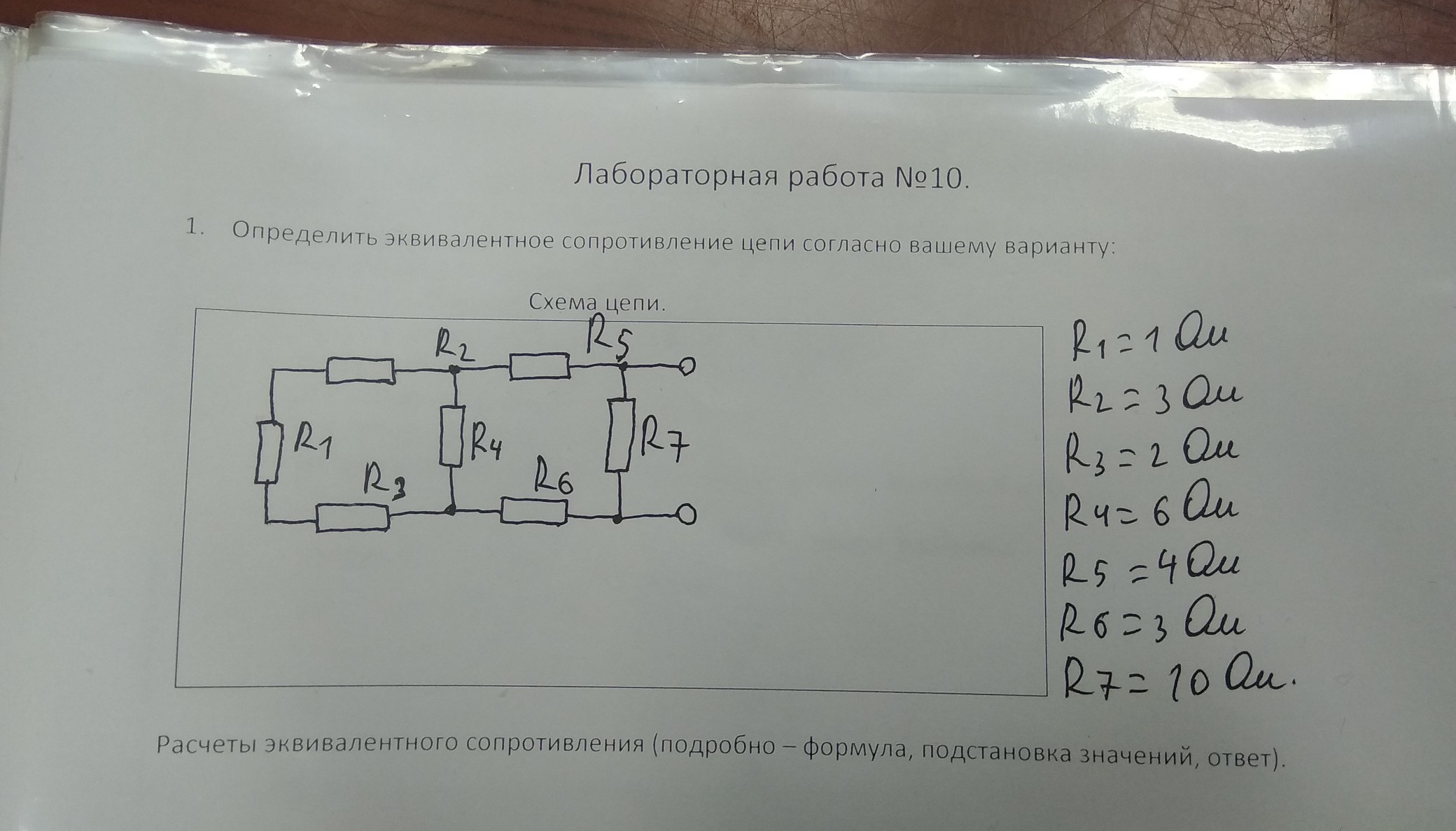
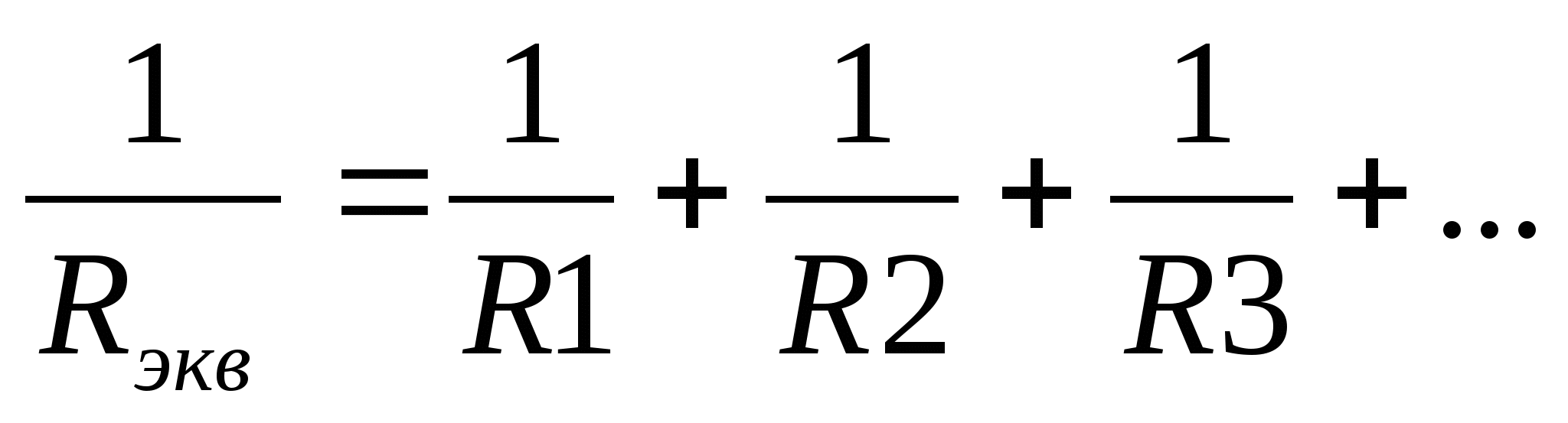- Дополнительные методы расчета цепей
- Постулаты Кирхгофа
- Первый постулат
- Второй постулат
- Параллельное соединение
- Эквивалентная схема
- Физические формулы и примеры вычислений
- Параллельное соединение
- Физические формулы и примеры вычислений
- Расчет параллельного соединения резисторов
- Емкость в цепи переменного тока
- Определение
- Практическое применение
- Простое соединение
- Практическое применение
- Простое соединение
- Комбинированный контур
- Виды пассивных элементов
- Катушка индуктивности
- Емкостной элемент
- Расчёт при смешанном соединении устройств
- Как рассчитать сложные схемы соединения резисторов
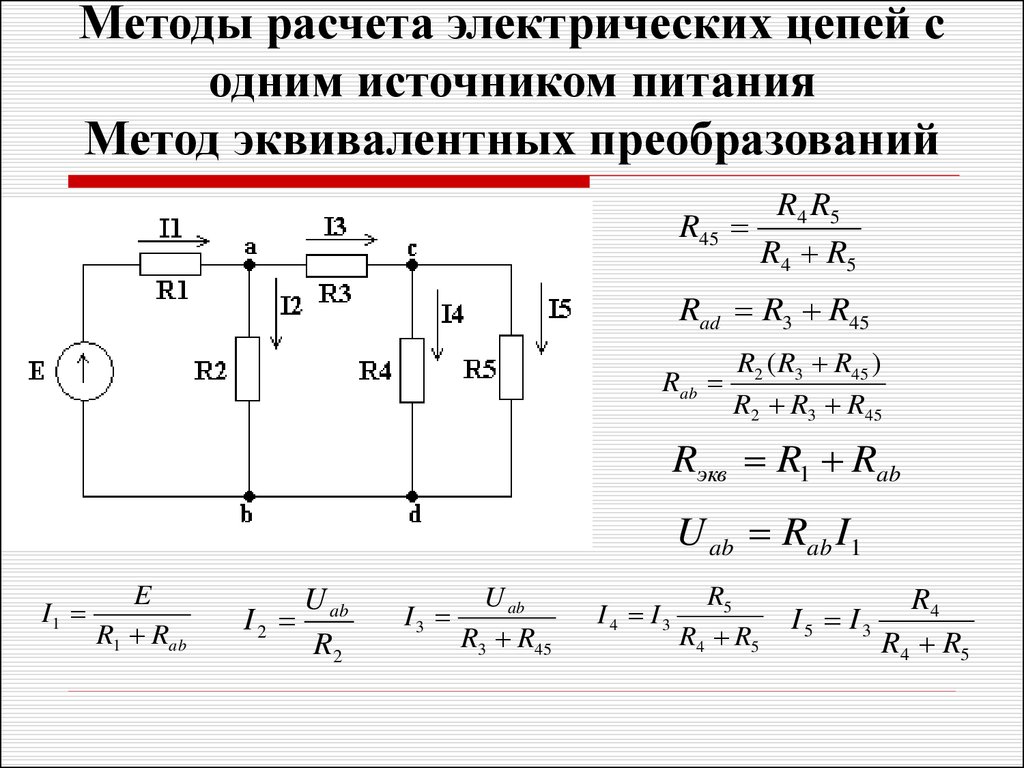
Дополнительные методы расчета цепей
Закон Кирхгофа
Все дополнительные методы расчета цепей в той или иной мере являются или основаны на первом и втором законах Кирхгофа. К этим методам относятся:
- Метод контурных токов – основан на введении дополнительных величин контурных токов, удовлетворяющих 1-му закону Кирхгофа;
- Метод узловых потенциалов – с его помощью находят потенциалы всех узлов схемы и затем по известным потенциалам токи во всех ветвях. Метод базируется на первом законе Кирхгофа;
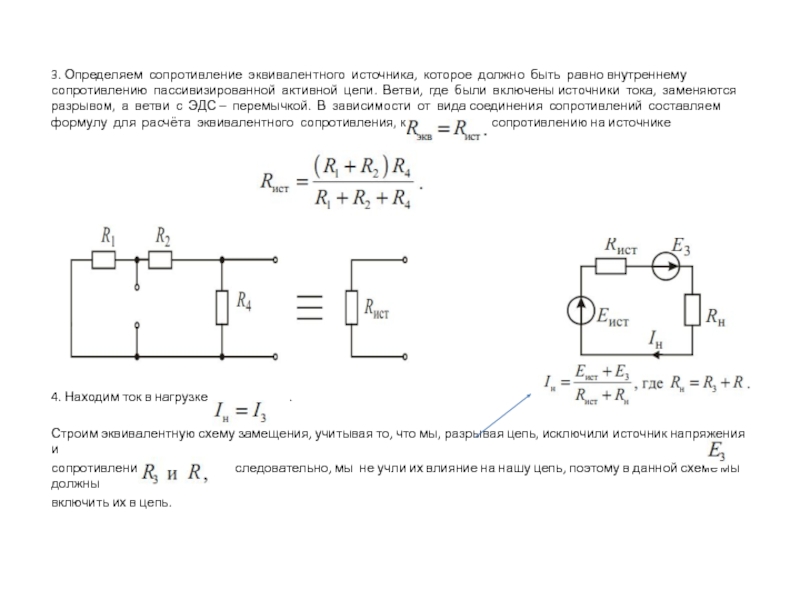
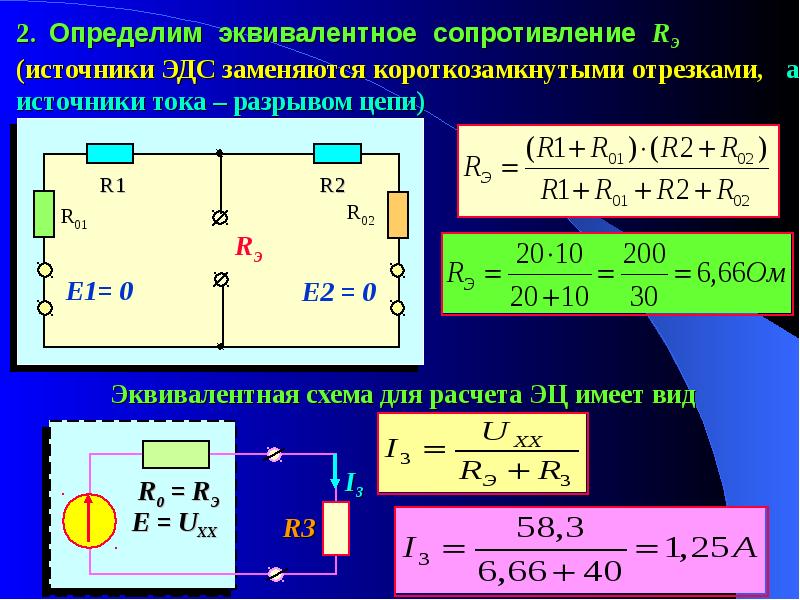
- Метод эквивалентного генератора – этот метод предоставляет решение задачи, как найти ток только в одной или нескольких ветвях. Суть метода в том, что любую электрическую цепь по отношению к исследуемой ветви можно представить в виде эквивалентного генератора;
- Метод наложения – основан на том, что ток в цепи или ветви схемы равен алгебраической сумме токов, наводимых каждым источником в отдельности.
Основная часть методов расчета направлена на упрощение процедуры определения токов в ветвях схемы. Эти мероприятия проводятся либо упрощением систем уравнений, по которым проводятся расчеты, либо упрощением самой схемы. Основываясь, в первую очередь, на постулаты Кирхгофа, любой из методов отвечает на вопрос: как определить силу тока и напряжение электрической цепи.
Постулаты Кирхгофа
Эти принципы используют для расчета сложных электрических схем. Базовые сведения о токах и напряжениях помогут уточнить контрольные параметры в отдельных узлах. С помощью этой информации корректируют характеристики отдельных функциональных компонентов. Они пригодятся для определения уровня выходного сигнала в определенных точках без применения измерительной аппаратуры.
Первый постулат
По классической формулировке сумма (алгебраическая) входящих и выходящих из одного узла токов определяется выражением:
i1 + i2 + … + in = 0.
Это соотношение справедливо для любой контрольной точки схемы, где соединяются ветви. Не имеет значения, какие именно компоненты включены в отдельные цепи:
- реактивные;
- пассивные;
- источники питания в любой полярности.
Второй постулат
Это правило определяет равенство сумм напряжений и ЭДС, включенных в один контур. Для наглядности можно представить простейший пример с двумя резисторами, подключенными к источнику постоянного тока. С помощью мультиметра измеряют напряжения на выводах:
- UR1 = 4 V;
- UR1 = 2,5 V;
- Uакб = 6,5 V = UR1 + UR2.
Второе правило действительно для всех замкнутых контуров, смешанных и сложных соединений. Для проверки вычислений можно суммировать последовательно разницу потенциалов контрольных точек. Если в цепи отсутствуют дополнительные генераторы (аккумуляторные батареи), получится результат, равный нулю. Выбирают направление обхода контура, соответствующее положительному току (входящему в узел). Выше показан частный случай, когда складывают результаты измерений.
К сведению. Второй постулат Кирхгофа применяют для расчета схем, подключенных к источнику питания переменного тока.
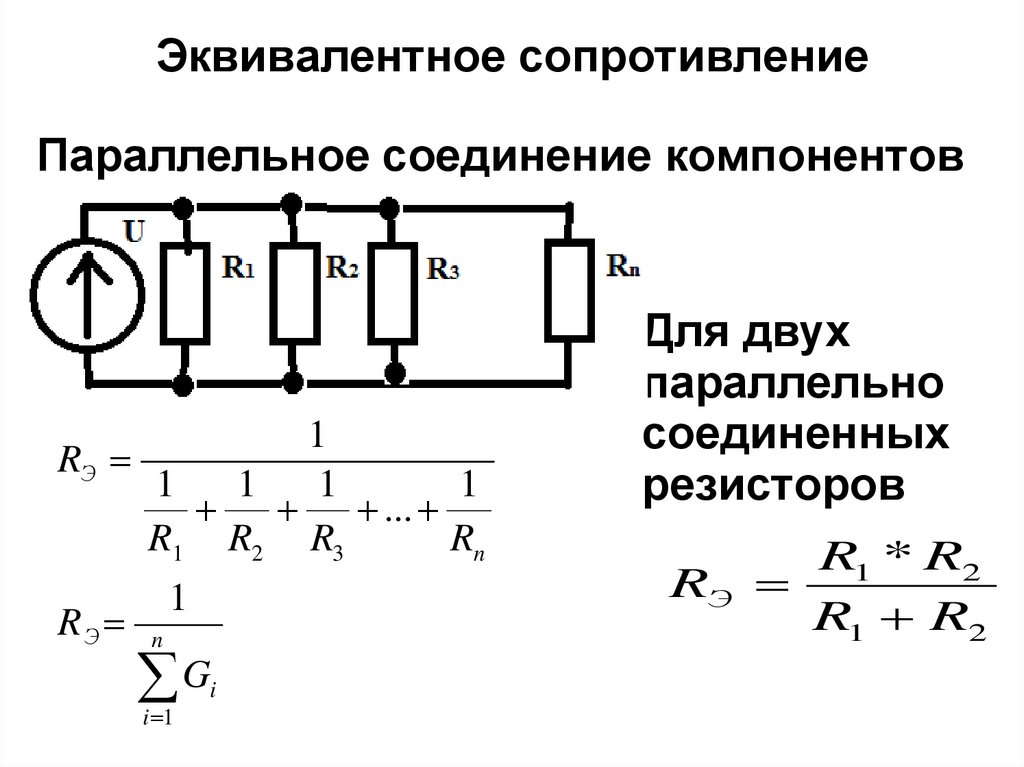
Параллельное соединение
Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
- общий ток: I = I1 + I2 + … + In;
- общее напряжение: U = U1 = U2 = … = Un;
- Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.
Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.
Эквивалентная схема
При расчётах сопротивления электрических цепей широко используется понятие «эквивалентная схема замещения». Её назначение — упростить сложную схему до вида, состоящую из минимума элементов. Иными словами, каждый сложный радиоэлемент можно представить в виде соответствующих ему эквивалентных простых радиодеталей: резистор, ёмкость, индуктивность, источники тока и напряжения. Это позволяет не только математически описать любую схему, но и рассчитать её параметры.
При этом обычно радиоэлементы идеализируются, то есть их паразитные параметры не учитываются. Так и для подсчёта сопротивления цепи каждый компонент представляется как идеальный резистор. После чего схема перерисовывается, и в результате на ней остаются только подключённые разными способами друг к другу резисторы.
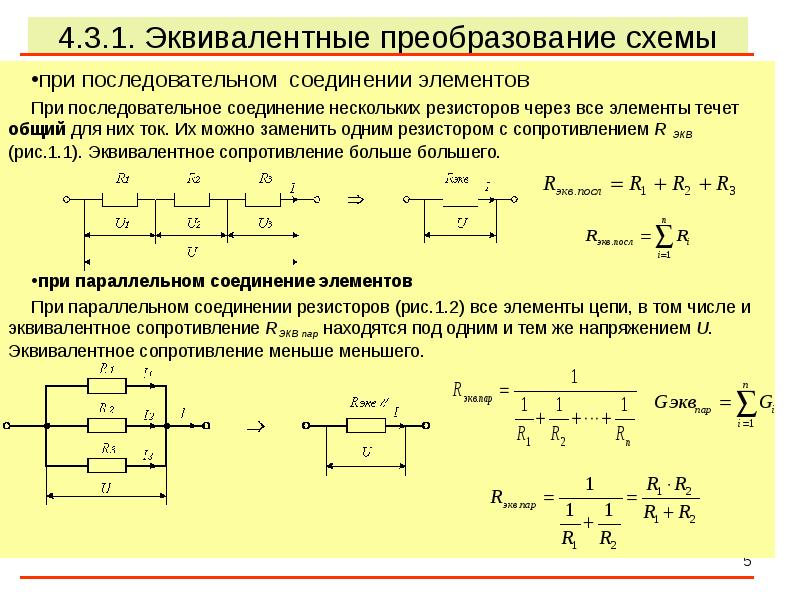
Существует два вида подключения:
- последовательное;
- параллельное.
Основными элементами электрической цепи являются узел, ветвь и контур. Узел — это место соединения двух и более ветвей. Ветвь — это последовательный участок цепи между двумя узлами, а контур — любая замкнутая цепь. Последовательное соединение состоит из элементов, при котором все компоненты цепи связаны так, что участок цепи, образованный из них, не имеет ни одного узла. А при параллельном соединении все компоненты электрической цепи контактируют между собой в двух узлах. При этом эти узлы напрямую не связаны.
Физические формулы и примеры вычислений
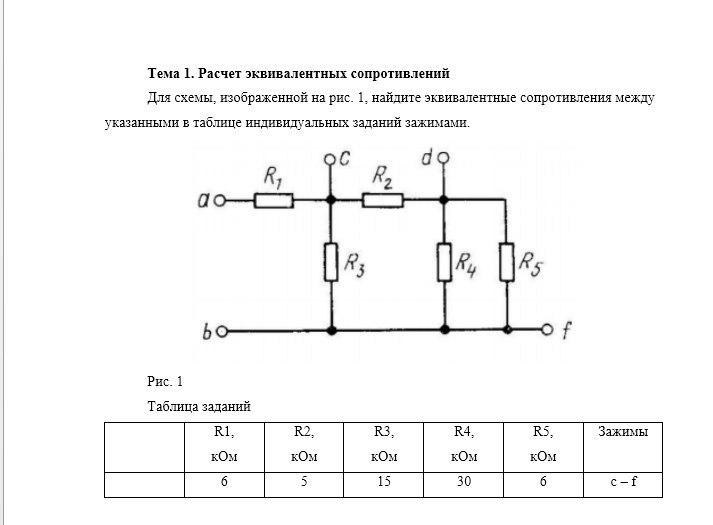
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
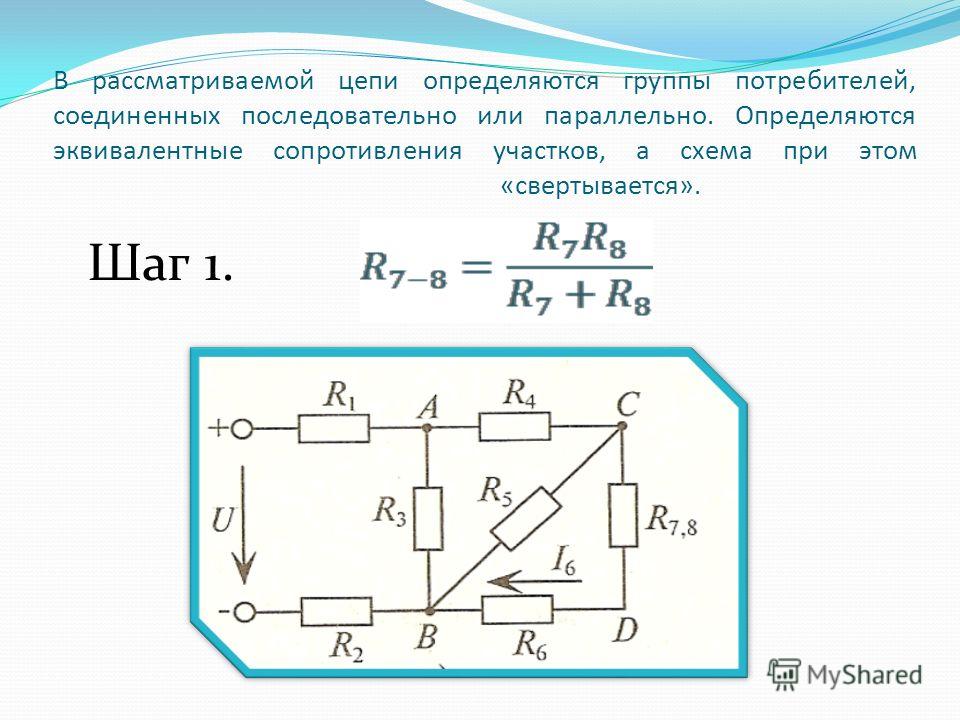
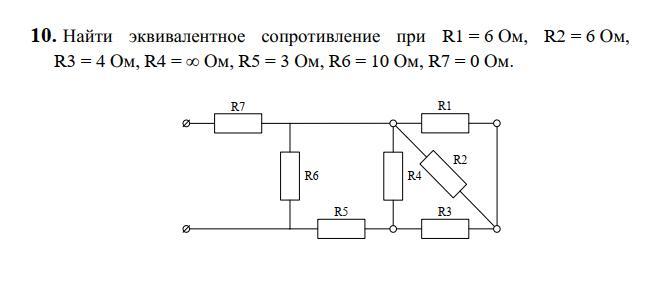
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
Требуется рассчитать токи на всех резистивных элементах.
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте. Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения
Делают расчёты для каждого такого звена, после – всей цепи целиком
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
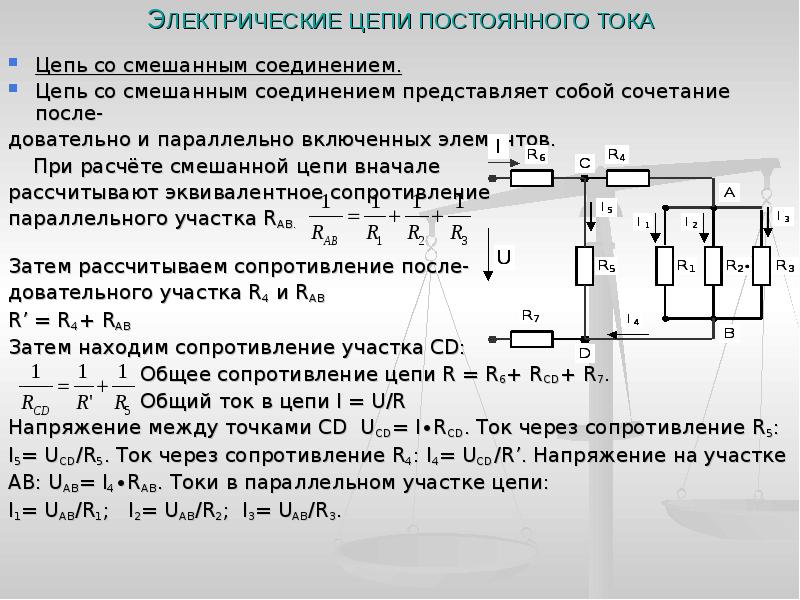
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Параллельное соединение
Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
- общий ток: I = I1 + I2 + … + In;
- общее напряжение: U = U1 = U2 = … = Un;
- Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.
Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
Требуется рассчитать токи на всех резистивных элементах.
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте. Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения
Делают расчёты для каждого такого звена, после – всей цепи целиком
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Расчет параллельного соединения резисторов
Для лучшего понимания процессов следует подробно рассмотреть представленную ниже схему. В контрольных точках (разрывах цепей) условно показаны измерительные приборы. Аналогичным образом подключают мультиметр для уточнения результатов теоретических вычислений. Чтобы не усложнять объяснение, использован «идеальный» источник постоянного тока. Его сопротивление в расчетах не учитывается. Аналогичным образом игнорированы емкостные (индуктивные) реактивные составляющие, которые способны создать незначительные нелинейные искажения.
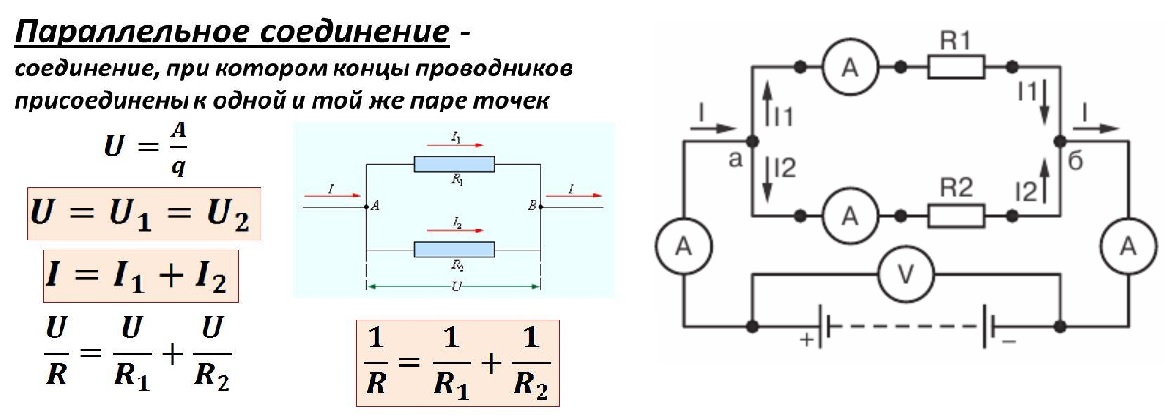 Электрическая схема с пояснительными формулами
Электрическая схема с пояснительными формулами
В рассматриваемом примере ток (I) идет по замкнутому контуру от положительного к отрицательному электроду АКБ. На входе параллельного участка (точка «а») он разделяется на I1 (I2), проходящие через разные ветки с электрическими сопротивлениями R1 (R2), соответственно. В точке «б» происходит объединение токов.
Если присоединить клеммы мультиметра к положительной клемме аккумулятора и входной точке, а после повторить измерение на выходе, будут определены одинаковые значения. Однако в отдельных ветвях токи будут отличаться, если применены разные сопротивления (R1≠R2). Сложение показаний подтвердит равенство суммы полученным ранее результатам измерений на входе (выходе). Промежуточный вывод, подтвержденный экспериментально:
Iобщ = I1 + I2.
Далее можно проверить разницу потенциалов на клеммах источника питания (Uип), в контрольных точках (Uаб) и на отдельных резисторах (UR1 и UR2). Несложно убедиться в том, что Uип = Uаб = UR1 = UR2. Для отдельных ветвей будут действительны пропорции:
- UR1 = I1 * R1;
- UR2 = I2 * R2.
Однако с учетом результатов измерений можно приравнять обе стороны выражений:
UR1 = UR2 = I1 * R1 = I2 * R2.
Простым преобразованием получают соотношение:
I1/I2 = R2/R1.
На основе этой формулы надо сделать следующий важный вывод: токи обратно пропорциональны электрическим сопротивлениям в соответствующих ветвях параллельной цепи.
Пример с исходными данными:
- батарейка Uип = 6V;
- сопротивление параллельных резисторов: R1 = 50 Ом, R2 = 150 Ом.
Расчет:
- найти ток в первой ветке можно по формуле: I1 = Uип / R1 = 6/50 = 0,12А = 120 мА;
- аналогичным образом вычисляют: I2 = Uип / R2 = 6/150 = 0,04А = 40 мА;
- суммарное значение: Iобщ = I1 + I2 = 120 + 40 = 160 мА;
- соблюдается отмеченный выше принцип пропорциональности: I1/I2 = R2/R1 = 50/150 = 40/120 ≈ 0,333.
Следует отметить разную силу тока в отдельных ветках. Для наглядности можно вспомнить пример с аналогом из водопроводных труб. В разветвленном участке по протоку с крупным диаметром пройдет больше жидкости, по сравнению с другим за контрольный временной интервал. Аналогичным образом действует электрическое сопротивление. При увеличении номинала пассивного элемента создаются дополнительные препятствия прохождению тока.
Для расчета сложных схем используют технологию эквивалентных сопротивлений. Этим термином обозначают расчетную величину (Rэкв), которая равна сумме измеряемых параметров отдельных компонентов на определенном участке цепи. Проще всего сделать вычисления, если соединить резисторы (номиналы из примера) последовательно:
Rэкв = R1 + R2 = 50 + 150 = 200 Ом.
Ниже подробно рассмотрен вариант с параллельной схемой:
- по закону Ома для всей цепи действительно выражение: Iобщ = Uип/ Rэкв;
- в отдельных ветках: I1 = U1/ R1 (I2 = U2/ R2);
- по закону Кирхгофа для каждого провода: I = I1+ I2;
- преобразование перечисленных соотношений позволяет сделать промежуточный вывод: Uип/ Rэкв = U1/ R1 + U2/ R2;
- с учетом равенства напряжений: Uип = U1 = U2, можно переделать предыдущую формулу следующим образом: Uип/ Rэкв = Uип / R1 + Uип / R2 = Uип (1/R1 + 1/R2);
- делением на общий множитель Uип получают итоговое выражение: 1/Rэкв = 1/R1 + 1/R2.
Последняя позиция позволяет сделать несколько важных заключений:
- общая проводимость (величина, обратная электрическому сопротивлению) равна сумме проводимостей параллельных участков цепи;
- эквивалентное сопротивление можно вычислить делением единицы на проводимость;
- Rэкв при параллельном соединении всегда меньше самого меньшего из пассивных компонентов цепи.
Емкость в цепи переменного тока
При подаче на конденсатор постоянного напряжения он постепенно зарядится до максимальной разности потенциалов на его обкладках. После этого ток через электронный компонент прекратится и, не считая ничтожной утечки, будет равняться нулю. Поэтому в цепи постоянного тока конденсатор имеет огромное сопротивление. При расчетах его величину принимают равной бесконечности.
Реактивное сопротивление имеет вполне исчисляемое значение. Его можно измерить с помощью осциллографа, генератора и постоянного резистора. Для этого потребуется собрать схему. В ней конденсатор образует с резистором делитель напряжения. С помощью осциллографа будет измеряться потенциал, который образуется на выводах ёмкости.
Для данной схемы вычисления имеют следующий вид.
Формула косвенного измерения
Здесь:
- Ur – разность потенциалов на резисторе, В;
- Uc – напряжение на обкладках, В;
- R – сопротивление резистора, ом;
- Xc – сопротивление ёмкости, ом;
- I – ток, протекающий в цепи, А.
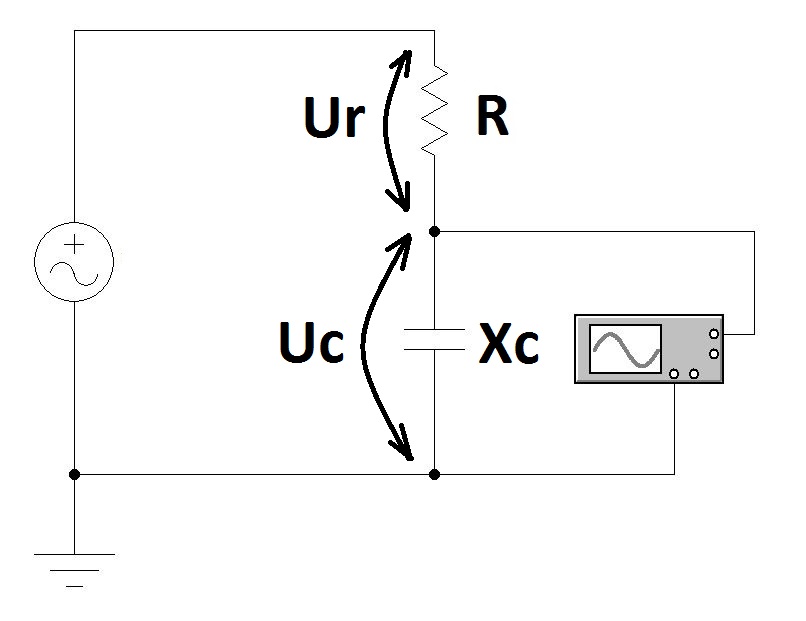 Косвенное измерение
Косвенное измерение
Важно! Электрический кабель также обладает ёмкостью. Поэтому после снятия напряжения на нём остаётся некоторый заряд
Данное явление опасно для человека, особенно, если проводник до отключения находился под потенциалом 1000 В и выше.
Определение
Если посчитать общее сопротивление (Rобщ), можно выяснить изменение основных электрических параметров (тока (I) и напряжения (U)) при подключении схемы к определенному источнику питания. В простейшем варианте достаточно применить закон Ома (I = U/ R) и пренебречь внутренним сопротивлением аккумулятора.
При напряжении U = 6,5 В через подключенный резистор R = 20 ОМ будет проходить ток I = 6,5/20 = 0,325 А. По вычисленному параметру с помощью классической формулы можно узнать мощность:
P = I2 *R = U2/ R = 0,105625 * 20 = 2,11 Вт.
Полученное значение пригодится для выбора подходящего пассивного элемента в ассортименте магазина.
На практике приходится решать задачи с большим количеством элементов. Общий показатель эквивалентен суммарному сопротивлению цепи. Однако простым сложением правильный результат получить нельзя. Ниже рассмотрены технологии, по которым выполняют корректные вычисления.
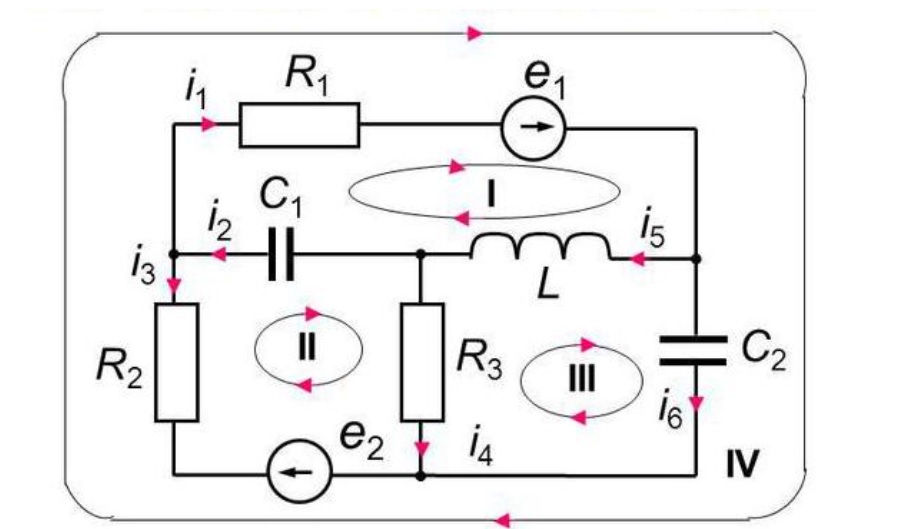 Основные термины и определения
Основные термины и определения
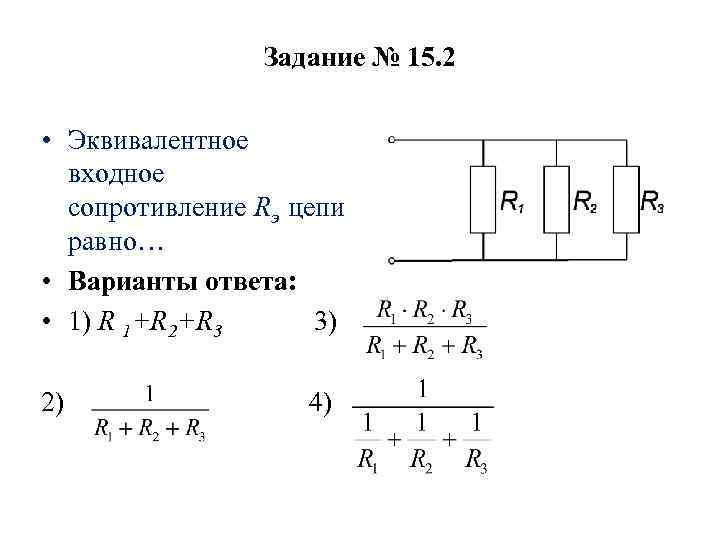
Рисунок поясняет используемую терминологию:
- i1, i2… i6 – токи в отдельных цепях;
- R1-R3 – пассивные элементы (резисторы);
- e1, e2 – типичные обозначения источников тока (ЭДС);
- L и C – компоненты с реактивными характеристиками (индуктивными и емкостными, соответственно);
- ветвями называют с одним током;
- места соединение этих цепей – узлы;
- контуры (обозначены римскими цифрами I, II и III) показывают замкнутые пути прохождения токов по нескольким ветвям.
Практическое применение
Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
Простое соединение
Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм. Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
Практическое применение
 Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
Простое соединение
 Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм. Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.
Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм. Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
Комбинированный контур
 Необходимо вычислить мощность и эквивалентное сопротивление смешанной цепи, состоящей из четырёх резисторов. Резистор R1 =R2 =5 Ом, R3= 10 Ом, R4 =3 Ом. На схему подаётся питание пять вольт.
Необходимо вычислить мощность и эквивалентное сопротивление смешанной цепи, состоящей из четырёх резисторов. Резистор R1 =R2 =5 Ом, R3= 10 Ом, R4 =3 Ом. На схему подаётся питание пять вольт.
Первоначально понадобится упростить схему. Сопротивления R3 и R4 включены относительно друг друга параллельно. Поэтому находится их объединённое сопротивление:
Rp = (R3*R4)/(R3+R4).
Rp = (10*3)/ (10+3) = 2,3 Ом.
Теперь схему можно перерисовать в виде трёх последовательно включённых резисторов и найти общее сопротивление путём сложения их величин:
Ro = R1+R2+Rp = 5+5+2,3 = 12,3 Ом.
Зная эквивалентное сопротивление, используя закон Ома, несложно вычислить силу тока в цепи и мощность эквивалентного резистора:
I = U/R = 5/2,3 = 2,2 A.
P = I*U = 2,2*5= 11 Вт.
Таким образом, путём постепенного упрощения схемы можно свести цепь из последовательно и параллельно соединённых резисторов к одному элементу. А затем рассчитать его сопротивление и требуемую мощность.
Виды пассивных элементов
Данные устройства характеризуются тем, что вместо рассеивания энергии склонны к ее накоплению. Разные типы таких деталей создают различные формы сопротивления.
Катушка индуктивности
Это радиокомпонент, представляющий собой проводниковый элемент спиральной или винтообразной формы, покрытый изоляцией. В схемах катушки используют для нивелирования помех и искажений, снижения величины переменного тока, генерации магнитного поля. Длинные тонкие элементы носят название соленоидов. Катушки отличаются небольшими величинами активной сопротивляемости и емкости, но обладают индуктивностью, генерируя электродвижущую силу.
 Подключение катушки в электрическую цепь
Подключение катушки в электрическую цепь
Емкостной элемент
Примером этого вида деталей является конденсатор. Он включает в себя две проводящие обкладки, между которыми находится диэлектрический материал. Протекание электротока обусловлено накоплением и отдачей обкладками своего заряда.
 Подсоединение конденсатора в электроцепь
Подсоединение конденсатора в электроцепь
Расчёт при смешанном соединении устройств
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Как рассчитать сложные схемы соединения резисторов
Если соединять большее количество элементов, надо в рассмотренные формулы добавить необходимое количество слагаемых.
Исходные данные:
- источник постоянного тока 12V;
- сопротивление параллельных резисторов, Ом: 10, 40, 60, 80.
Расчет:
- основная формула: 1/Rэкв = 1/R1 + 1/R2 + 1/R3 + 1/R4;
- подставив исходные данные, вычисляют проводимость: G = 1/Rэкв =1/10 + 1/40 + 1/60 +1/80 = 0,1 + 0,025 + 0,0166 +0,0125 = 0,1541;
- эквивалентное сопротивление: Rэкв = 1/0,1541 ≈ 6,5 Ом;
- ток в цепи: Iобщ = Uип/ Rэкв = 12/ 6,5 ≈ 1,85 А.
 Сложные схемы
Сложные схемы
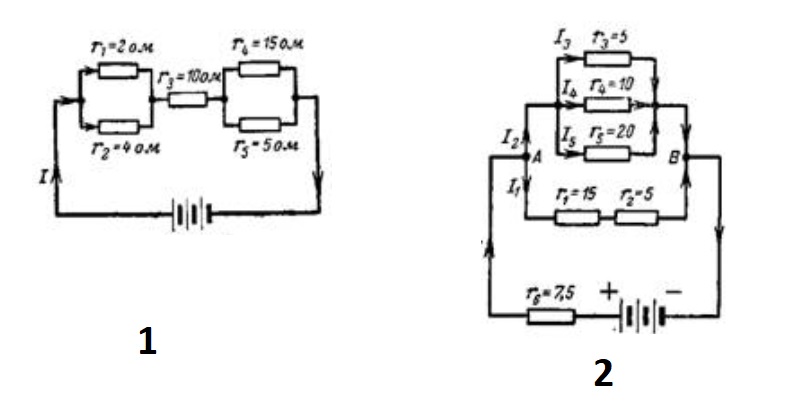
По аналогичной технологии делают расчеты более сложных цепей. На рисунке обозначены номиналы сопротивлений. В обоих случаях применяется одинаковый источник питания с Uип = 12V.
Расчет 1 (последовательное и параллельное соединение):
- для каждого параллельного участка можно использовать формулу: Rобщ = 1/ (1/R1 + 1/R2) = R1*R2/R1 + R2;
- эквивалентное сопротивление первой части: Rэкв1 = (2*4)/ (2+4) = 1,3 Ом;
- второй: Rэкв2 = (15*5)/ (15+5) = 3,75 Ом;
- общее: Rэкв = 1,3 + 10 + 3,75 = 15,05 Ом;
- Iобщ = Uип/ Rэкв = 12/ 15,05 ≈ 0,8 А.
Расчет 2 (сложное параллельное соединение):
- в этом варианте сначала вычисляют проводимость части (R3, R4, R5) по формуле: G345 = 1/5 + 1/10 + 1/ 20 =7/20 = 0,35 сим;
- Rэкв (345) = 1/0,35 ≈ 2,857 Ом;
- суммарное значение для цепи: R1 + R2 = 20 Ом;
- по аналогии с предыдущим способом определяют: G12345 = 0,4 сим и Rэкв(12345) = (20*2,857)/ 20 + 2,857) ≈ 2,5 Ом;
- после добавления последнего элемента (R6=7,5 Ом) получают итоговый результат: Rэкв = 2,5 + 7,5 = 10 Ом;
- делением определяют силу тока в нагрузке, подключенной к источнику тока 12 V: I = 12/10 = 1,2 А.
В последнем примере применен дополнительный компонент цепи (R6). Соответственно, для этой схемы не будет выполняться рассмотренная выше пропорция равенства напряжений (источника и на подключенной нагрузке).
В этом случае разница потенциалов на шестом резисторе составит:
U6 = I *R6 = 1,2 * 7,5 = 9 В.
Соответственно, изменится напряжение между контрольными точками:
Uав = I * Rэкв(12345) = 1,2*2,5 = 12-9 =3V.
Вторая часть формулы демонстрирует проверку вычитанием напряжений (Uип – U6).