Закон полного тока

Закон ома для полной цепи

Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.

Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.

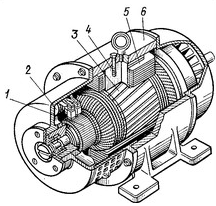
Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта. Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания. Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.

Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока. По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами. Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет разность потенциалов.

Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела. Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r). На размеры силы тока влияет такое понятие, как электродвижущая сила – ЭДС, прилагаемая к электродам, обозначенная символом Е.

Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U

ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока. В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы. Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода.

Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка.

9.1.4. Неразветвленная магнитная цепь

Задачей расчета
неразветвленной магнитной цепи в большинстве случаев является определение МДС F= Iw, необходимой для того, чтобы получить
заданные значения магнитного потока или магнитной индукции в некотором участке магнитопровода (чаще всего в воздушном зазоре).

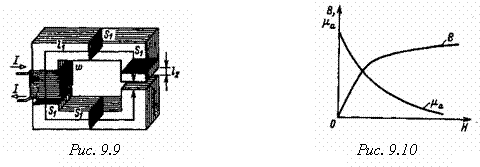
На рис. 9.9 приведен пример
неразветвленной магнитной цепи — магнитопровод
постоянного поперечного сечения S₁ с зазором. На этом же рисунке указаны другие
геометрические размеры обоих участков магнитопровода:
средняя длина l₁
магнитной линии первого участка из ферромагнитного материала и длина l₂ второго участка — воздушного зазора. Магнитные свойства
ферромагнитного материала заданы основной кривой намагничивания В(Н) (рис. 9.10) и тем самым по (9.4)
зависимостью m_a(Н).

По закону полного тока (9.2)

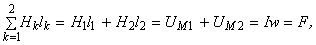
где H₁ и H₂ — напряженности магнитного поля в первом и втором
участках.

В воздушном зазоре значения
магнитной индукции В₂ и
напряженности H₂
связаны простым соотношением В₂ = mН₂, а для участка из ферромагнитного
материала В₁ = m_a1 Н₁.

Кроме того, в неразветвленной
магнитной цепи магнитный поток одинаков в любом поперечном сечении магнитопровода:

Ф
= В₁S₁ =B₂S₂, (9.6)

где S₁ и S₂ — площади поперечного сечения участка из ферромагнитного
материала и воздушного зазора.

Если задан магнитный поток Ф, то по (9.6) найдем значения индукций B₁ и B₂. Напряженность поля H₁ определим по основной кривой намагничивания (рис. 9.10), аH₂= B₂m. Далее по (9.5) вычислим необходимое значение МДС.

Сложнее
обратная задача: расчет магнитного потока при заданной
МДС F.

Заменив в (9.5) напряженности
магнитного поля значениями индукции, получим

,

или с учетом (9.6)

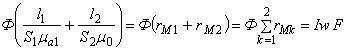
где r_Mk= l_kS_km_ak — магнитное сопротивление k-гoучастка магнитной цепи, причем магнитное сопротивление k-гo участка нелинейное, если зависимость В(H) для этого участка нелинейная (рис. 9.10), т.е. m_ak≠ const.

Для участка цепи с нелинейным
магнитным сопротивлением r_Mможно построить вебер-амперную характеристику — зависимость
магнитного потока Ф от магнитного напряжения U_Mна этом участке магнитопровода.
Вебер-амперная характеристика участка магнитопровода
рассчитывается по основной кривой намагничивания ферромагнитного материала В(H). Чтобы построить вебер-амперную характеристику, нужно ординаты и
абсциссы всех точек основной кривой намагничивания умножить соответственно на
площадь поперечного сечения участка Sи его среднюю длину l.

На рис. 9.11 приведены
вебер-амперные характеристики Ф(U_M1) для ферромагнитного участка с нелинейным магнитным
сопротивлением r_M1 и Ф(U_M2) для воздушного зазора с постоянным магнитным сопротивлением r_M2 = l₂ S₂m магнитопровода по
рис. 9.9.

Между расчетами нелинейных
электрических цепей постоянного тока и магнитных цепей с
постоянными МДС нетрудно установить аналогию.
Действительно, из уравнения (27.7) следует, что магнитное напряжение на участке
магнитной цепи равно произведению магнитного сопротивления участка на магнитный
поток U_M = r_MФ. Эта зависимость аналогична закону Ома
для резистивного элемента электрической цепи постоянного тока U = rI.
Сумма магнитных напряжений в контуре магнитной цепи равна сумме МДС этого
контура SU_M = SF, что аналогично второму закону Кирхгофа для электрических цепей
постоянного тока SU = SE.

Продолжая дальше аналогию
между электрическими цепями постоянного тока и магнитными цепями с постоянными МДС, представим неразветвленную
магнитную цепь (рис. 9.9) схемой замещения (рис. 9.12, а).

В качестве иллюстрации
ограничимся применением для анализа неразветвленной магнитной цепи графических
методов: метода сложения вебер-амперных характеристик (рис. 9.11) и метода нагрузочной
характеристики (рис. 9.12, б).

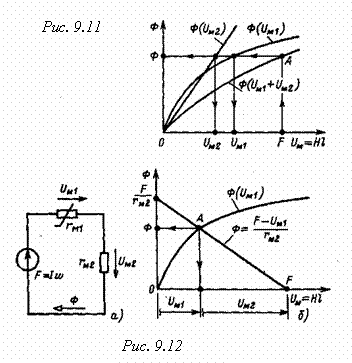
Согласно первому методу
построим вебер-амперную характеристику всей неразветвленной магнитной цепи Ф(U_M1 + U_M2), графически складывая по напряжению вебер-амперные
характеристики ее двух участков. При известной МДС F= Iwпо вебер-амперной характеристике всей магнитной цепи
определим рабочую точку А, т. е. магнитный поток Ф,
а по вебер-амперным характеристикам участков магнитопровода
— магнитные напряжения на каждом из них.

Согласно второму методу для
второго (линейного) участка построим нагрузочную характеристику

т. е. прямую, проходящую
через точку Fна оси абсцисс
и точку Fr_M2на оси ординат. Точка пересечения А нагрузочной
характеристики с вебер-амперной характеристикой ферромагнитного участка цепи Ф(U_M1) определяет магнитный поток Ф в цепи и магнитные
напряжения на ферромагнитном участке U_M1 и воздушном зазоре U_M2. Значение индукции в воздушном зазоре B₂ = Ф/S₂.

Определение полного тока

Сутью данного закона является определение взаимной связи между электрическим током и образованным его протеканием магнитным полем. Эта особенность выявлена экспериментальным путем в первой половине XIX века. Позднее была создана формулировка, устанавливающая закон полного тока для магнитного поля. Классическое определение приведено ниже. Однако начинать изучение темы следует с базовых принципов.

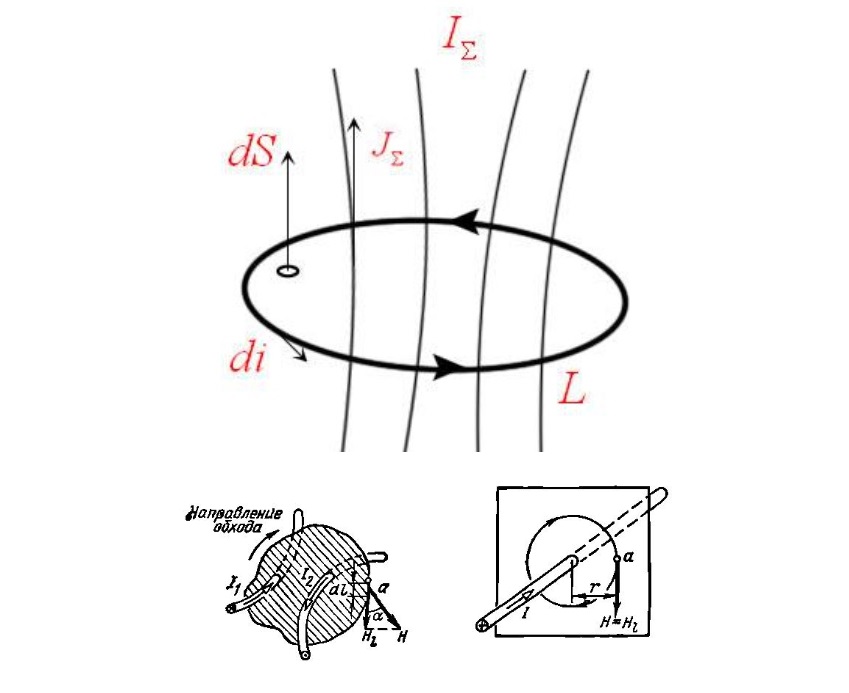Схематическое изображение физических параметров

На рисунке отмечены следующие компоненты:

• I∑ – суммарный (полный) ток;
• S – пронизываемая (dS – элементарная) площадка;
• dL – элементарный линейный участок.
• J∑ – плотность распределения токов;
• L – кольцевой замкнутый контур;
• H – напряженность магнитного поля в векторном представлении.

Основные понятия

В соответствии с рассматриваемым законом для расчета магнитных полей применяется следующий упрощенный подход. Полный ток представляется в виде суммы нескольких составляющих, протекающих через поверхность, охватываемую замкнутым контуром L. Теоретические выкладки могут быть представлены следующим образом:

1. Полный электрический поток, пронизывающих конур Σ I – это векторная сумма I1 и I2.
2. В рассматриваемом примере для его определения используется формула:
   ΣI = I1- I2 (минус перед вторым слагаемым означает, что направления токов противоположны).
3. Они, в свою очередь, определяются по известному в электротехнике закону (правилу) буравчика.

Напряженность магнитного поля вдоль контура вычисляется на основании полученных выкладок по специальным методикам. Для ее нахождения придется проинтегрировать этот параметр по L, используя уравнение Максвелла, представленное в одной из форм.Оно может быть применено и в дифференциальной форме, но это несколько усложнит выкладки.

Упрощенный подход в интегральном виде

Если воспользоваться дифференциальным представлением – выразить закон полного тока в упрощенном виде будет очень сложно (в этом случае в него приходится вводить дополнительные компоненты). Добавим к этому, что магнитное вихревое поле, создаваемое движущимся в пределах контура токами, определяется в этом случае с учетом тока смещения, зависящего от скорости изменения электрической индукции.

Поэтому на практике в ТОЭ большей популярностью пользуется представление формул для полных токов в виде суммирования микроскопически малых отрезков контура с создаваемыми в них вихревыми полями. Этот подход предполагает применение уравнения Максвелла в интегральной форме. При его реализации контур разбивается на мелкие отрезки, в первом приближении считающиеся прямолинейными (согласно закону предполагается, что магнитное поле однородно). Эта величина, обозначаемая как Um для одного дискретного участка длиной ΔL магнитного поля, действующего в вакууме, определяется так:

Um= HL*ΔL

Суммарная напряженность вдоль полного контура L, представленная кратко в интегральном виде, находится по следующей формуле:

UL= Σ HL*ΔL.

Закон полного тока для вакуума

В окончательном виде, оформленном по всем правилам интегрирования, закон полного тока выглядит так. Циркуляция вектора «В» по замкнутому контуру может быть представлена как произведение магнитной постоянной m на сумму токов:

Интеграл от B по dL = интегралу от Bl по dL= m Σ In

где n – это обще число проводников с разнонаправленными токами, охватываемыми мысленно представляемым контуром L произвольной формы.

Каждый ток учитывается в этой формуле столько раз, сколько он полностью охватывается данным контуром.

На окончательный вид полученных выкладок для закона полного тока большое влияние оказывает среда, в которой действует наведенная электромагнитная сила (поле).

Определение закона полного тока

Важные выводы и пояснения:

• напряженность зависит от источника тока;
• индукция выполняет силовые функции воздействия на движущиеся по цепи заряды;
• параметры поля формируются магнитными свойствами определенной среды.

На практике усиление тока сопровождается пропорциональным изменением поля (магнитной индукции). Базовое правило справедливо при рассмотрении цепей, созданных из серебра, влажного или сухого воздуха, других материалов.

Измененные правила действуют в железе или иной среде с выраженными ферромагнитными свойствами. Именно такие решения применяют при создании трансформаторов и других изделий для улучшения потребительских характеристик.

Для упрощения следует начать изучение физических величин и расчетов на примере нейтральной среды. При отсутствии ферромагнитных параметров можно изобразить магнитное поле несколькими замкнутыми линиями длиной L. В этом случае полный ток (I) будет зависеть от индукции (B) следующим образом:

I = (B*L)/м.

Здесь m – магнитная постоянная, которая в стандартной системе единиц измерения приблизительно равна 1,257*10-7 Генри на метр (Гн/м).

Важно! В действительности подобные идеальные условия встречаются редко, когда индукция сохраняет одинаковые параметры вдоль всей линии контура. Поле формируется перпендикулярно прямому длинному проводнику

Его линии образуют набор из множества окружностей. Центр каждой из них соответствует продольной оси проводника. Расстояние от нее до кольца – r. Длину (L) вычисляют по стандартной геометрической пропорции:

Поле формируется перпендикулярно прямому длинному проводнику. Его линии образуют набор из множества окружностей. Центр каждой из них соответствует продольной оси проводника. Расстояние от нее до кольца – r. Длину (L) вычисляют по стандартной геометрической пропорции:

L = 2π*r.

Если разместить витки симметрично на тороидальном сердечнике из электрически нейтрального фарфора для устранения искажений, линии магнитного поля будут проходить внутри равномерно. Кольца, как показано на рисунке с вырезанным сегментом, образуют замкнутые контуры. В такой конструкции обеспечивается неизменность индукции. Для каждой отдельной линии можно пользоваться формулой:

B*L = B* 2π*r = m*I.

Суммарное значение (полный ток) получают умножением на количество витков (N).

На основе приведенных данных нетрудно вычислить индукцию, которая будет создана внутри нейтрального тороидального кольца при определенной силе тока:

B = m*(I*N/L).

Эта пропорция позволяет сделать определение удельного полного тока:

(IN)o=(I*N)/L.

Зная размеры тора и другие исходные параметры, вычисляют индукцию у внутреннего и наружного края. При необходимости делают коррекции с помощью изменения толщины кольца, количества витков.

Если на основу из ферромагнитного материала намотать две обмотки (изолированные), будут создан наглядный образец для измерений. Изменяя силу тока в одном проводнике, можно наблюдать за изменением электродвижущей силы по подключенному к другой паре выводов прибору.

На графике приведены результаты эксперимента при использовании кольца, сделанного из железа с минимальным количеством примесей. Если применить закон полного тока для рассмотренного выше примера с нейтральным сердечником в точке «а», должно получиться приблизительно 5*10-4 Тл. Между тем в действительности напряженность составляет для этой силы тока 1,2 Тл при одинаковых размерах тока и количестве сделанных витков.

Корректируют вычисления с учетом поправочного коэффициента – магнитной проницаемости. Следует подчеркнуть, что это параметр не линейный. Максимальный полезный эффект наблюдается при относительно небольших значениях силы тока. Значительный спад после порогового уровня насыщения ограничивает практическое применение рассмотренных свойств.

9.1.1. Элементы магнитной цепи

Магнитной цепью (магнитопроводом) называется совокупность различных
ферромагнитных и неферромагнитных частей электротехнических устройств для создания магнитных полей нужных конфигурации и
интенсивности. В зависимости от принципа действия электротехнического
устройства магнитное поле может возбуждаться либо постоянным магнитом, либо
катушкой с током, расположенной в той или иной части магнитной цепи.

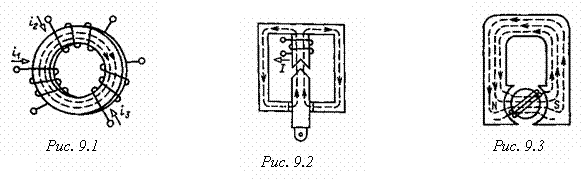
К простейшим магнитным цепям
относится тороид из однородного ферромагнитного
материала (рис. 9.1). Такие магнитопроводы
применяются в многообмоточных трансформаторах, магнитных усилителях, в
элементах ЭВМ и других электротехнических устройствах.

На рис. 9.2 показана
более сложная магнитная цепь электромеханического устройства, подвижная часть
которого втягивается в электромагнит при постоянном (или переменном) токе в
катушке. Сила притяжения зависит от положения подвижной части магнитопровода.

На рис. 9.3 изображена
магнитная цепь, в которой магнитное поле возбуждается постоянным магнитом. Если
подвижная катушка, расположенная на ферромагнитном цилиндре, включена в цепь
постоянного тока, то на нее действует вращающий момент. Поворот катушки с током
практически не влияет на магнитное поле магнитной цепи. Такая магнитная цепь
есть, например, в измерительных приборах магнитоэлектрической системы.

Рассмотренные магнитные цепи,
как и другие возможные конструкции, можно разделить на неразветвленные
магнитные цепи (рис. 9.1 и 9.3), в которых магнитный поток в любом сечении цепи
одинаков, и разветвленные магнитные цепи (рис. 9.2), в которых магнитные потоки
в различных сечениях цепи различны. В общем случае разветвленные магнитные цепи
могут быть сложной конфигурации, например в электрических двигателях,
генераторах и других устройствах.

В большинстве случаев
магнитную цепь следует считать нелинейной, и лишь при определенных допущениях и
определенных режимах работы магнитную цепь можно считать линейной.

Суть закона

Рассматриваемый закон, применимый в магнитных цепях, определяет следующую количественную связь между входящими в него составляющими. Циркуляция вектора магнитного поля по замкнутому контуру пропорциональна сумме токов, пронизывающих его. Чтобы понять физический смысл закона полного тока – потребуется ознакомиться с графическим представлением описываемых им процессов.

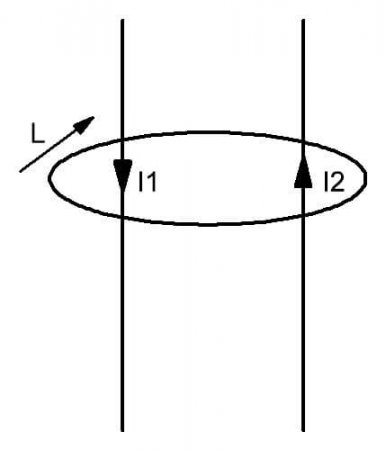
Из рисунка видно, что около двух проводников с протекающими по ним токами I1 и I2 образуется поле, ограниченное контуром L. Оно вводится как мысленно представляемая замкнутая фигура, плоскость которой пронизывают проводники с движущимися зарядами. Простыми словами этот закон можно выразить так. При наличии нескольких потоков электричества через мысленное представляемую поверхность, охватываемую контуром L, в ее пределах формируется магнитное поле с заданным распределением напряженности.

За положительное направление движения вектора в соответствии с законом для контура магнитной цепи выбирается ход часовой стрелки. Оно также является мысленно представляемым.

Такое определение создаваемого токами вихревого поля предполагает, что направление каждого из токов может быть произвольным.

Для справки! Вводимую полевую структуру и описывающий ее аппарат следует отличать от циркуляции электростатического вектора «Е», который при обходе контура всегда равен нулю. Вследствие этого такое поле относится к потенциальным структурам. Циркуляция же вектора «В» магнитного поля никогда не бывает нулевой. Именно поэтому оно называется «вихревым».

Формула закона полного тока

В этом разделе приведены формулы для уточненных расчетов и примеры типовых конструкций. Для интегральных вычислений вполне подходит закон Гаусса, который применяют в электростатике.

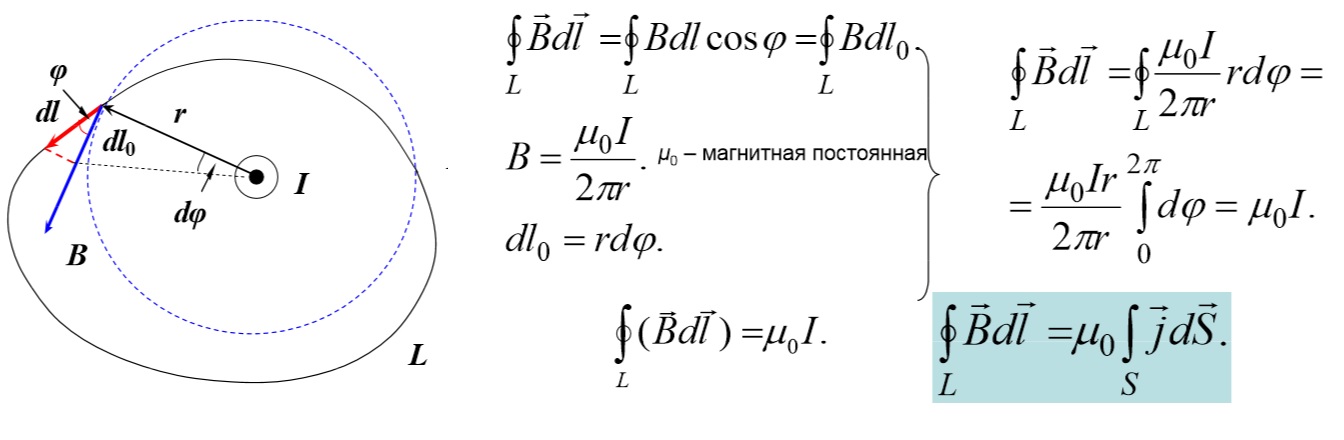Интегральная формула закона полного тока

Пояснения:

• L – обозначает замкнутый контур, созданный по произвольной траектории;
• векторы В и r направлены перпендикулярно;
• dl (dl0) – элементы произвольной части (силовой линии), соответственно;
• ϕ – угол между элементами.

Из формулы на рисунке понятно, что циркуляция вектора индукции не равняется нулю. Такие поля называют «соленоидальными» или вихревыми. В отличие от электродинамики, в данном случае отсутствуют потенциальные характеристики. Как и в базовом определении, полный ток определяется циркуляцией магнитной индукции (векторное выражение) по контуру произвольной формы, окружающему сумму токов.

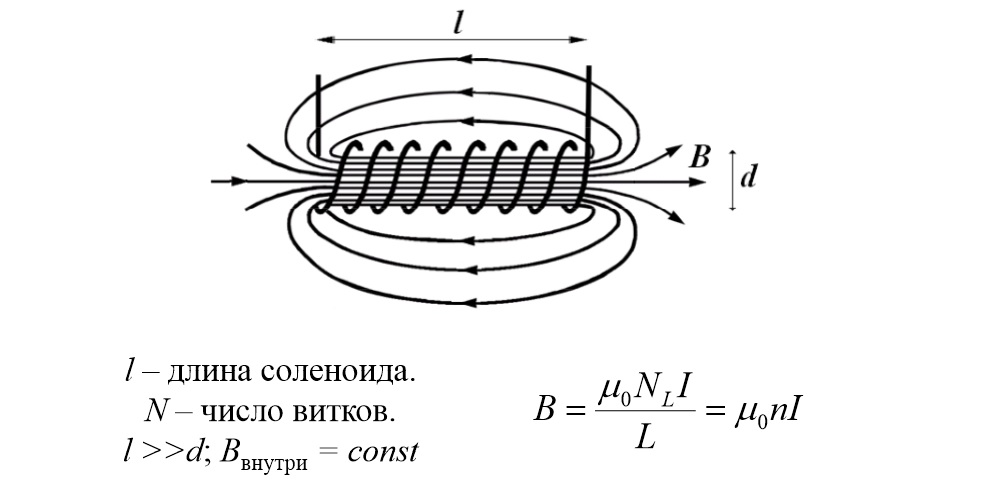Формула для расчета индуктивности, которую создает длинный соленоид

В этом примере n – число витков обмотки на единицу длины основы.

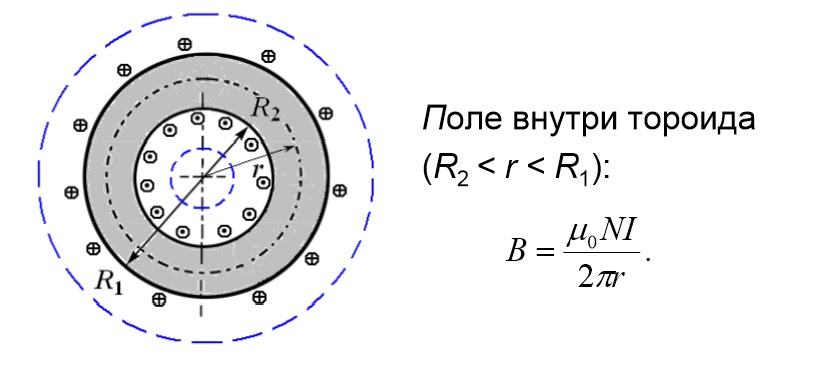Расчет параметров поля внутри тороида

Параметры:

• количество сделанных витков – N;
• внешний, внутренний и произвольный радиусы – R1, R2 и r.

Следует помнить! Вне тороида магнитное поле равно нулю.

Рассмотренные методики расчетов применяют с учетом реальных условий. Особое значение при выборе компонентов конструкций уделяют ферромагнитным свойствам сердечника. Проводники для обмоток выбирают с запасом, учитывая максимальную силу тока источника.

Закон в интегральном представлении

Рассмотрим бесконечно прямой проводник, по которому циркулирует электрический ток, образующий поле, ограниченное контуром в виде окружности. Плоскость, пронизывающая проводник, – это круг, очерчённый линией данной окружности (см. рис. 1).

Рис. 1. Поле бесконечно прямого тока

Воспользуемся методом разбиения контура на мизерные участки dl (элементарные векторы длины контура).  Пусть φ – угол между векторами dl и B. В нашем случае, при суммировании отрезков, вектор индукции B поворачивается так, что он очерчивает круг, то есть угол φ → 2π.

Из теоремы Остроградского-Гаусса вытекает формула:

Учитывая, что cos φ = 1,

следовательно:

Данная формула – постулат, подтверждённый экспериментально. Согласно этому постулату, циркуляция вектора B по окружности, то есть по замкнутому контуру, равна μ0I, где μ0 = 1/c2 ε0 – магнитная постоянная.

Ориентация вектора dB определяется путём применения правила буравчика. Это направление всегда перпендикулярно вектору плотности. Если проводников будет несколько (например, N), тогда

Каждый ток, с учётом знака, необходимо учитывать такое количество раз, которое соответствует числу его охватов контуром.

Ток берётся со знаком «+», если он по направлению обхода образует правовинтовую систему. При этом, отрицательным считается ток противоположного направления.

Заметим, что формула справедлива только для вакуума. В обычных условиях необходимо учитывать проницаемость среды.

Если ток распределён в пространстве (произвольный ток), тогда

где S – натянутая на контур поверхность, j – объёмная плотность тока. С учётом последнего выражения, формулу полного тока в вакууме можно записать:

Рис. 2. Иллюстрация закона для вакуума

Отсюда вытекает:

1. Закон справедлив не только для бесконечно прямолинейного проводника, но и для контуров, произвольной конфигурации.
2. Циркуляция вектора магнитной индукции B сориентированного вдоль магнитных линий, всегда отлична от нуля.
3. Ненулевая циркуляция свидетельствует о том, что магнитное поле прямолинейного, бесконечно длинного проводника не потенциально. Такое поле называют вихревым, либо соленоидным.

Формула закона полного тока

В этом разделе приведены формулы для уточненных расчетов и примеры типовых конструкций. Для интегральных вычислений вполне подходит закон Гаусса, который применяют в электростатике.

Пояснения:

• L – обозначает замкнутый контур, созданный по произвольной траектории;
• векторы В и r направлены перпендикулярно;
• dl (dl0) – элементы произвольной части (силовой линии), соответственно;
• ϕ – угол между элементами.

Из формулы на рисунке понятно, что циркуляция вектора индукции не равняется нулю. Такие поля называют «соленоидальными» или вихревыми. В отличие от электродинамики, в данном случае отсутствуют потенциальные характеристики. Как и в базовом определении, полный ток определяется циркуляцией магнитной индукции (векторное выражение) по контуру произвольной формы, окружающему сумму токов.

В этом примере n – число витков обмотки на единицу длины основы.

Параметры:

• количество сделанных витков – N;
• внешний, внутренний и произвольный радиусы – R1, R2 и r.

Следует помнить! Вне тороида магнитное поле равно нулю.

Рассмотренные методики расчетов применяют с учетом реальных условий. Особое значение при выборе компонентов конструкций уделяют ферромагнитным свойствам сердечника. Проводники для обмоток выбирают с запасом, учитывая максимальную силу тока источника.

§ 37. Закон полного тока

На рис. 80 показан проводник с током I, пронизывающий поверхность, ограниченную замкнутым контуром в виде окружности. Пусть центр окружности лежит на оси проводника. В пространстве, окружающем проводник с током, возникает магнитное поле. Так как отдельные точки контура находятся от проводника на равных расстояниях, то напряженность поля, созданная током в каждой точке контура, будет также одинаковой. Направление вектора напряженности поля H зависит от направления тока в проводнике и определяется по «правилу буравчика». Вектор H располагается по касательной к окружности контура.

Рис. 80. К закону полного тока

Путем опытов и расчетов установлено, что произведение напряженности поля H в точках контура на длину этого контура l равно току I, пронизывающему поверхность, ограниченную данным контуром.

Таким образом,

H ⋅ l = I.

В общем случае поверхность могут пронизывать несколько токов. Тогда определяют так называемый полный ток, т. е. находят алгебраическую сумму токов (∑I). Для этого случая можно записать:

H ⋅ l = ∑I.

Это выражение носит название закона полного тока. Закон полного тока является основным законом при расчете магнитных цепей и дает возможность в некоторых случаях легко определить напряженность поля.

Например, применив закон полного тока для определения напряженности магнитного поля в то на стоянии r от бесконечно длинного прямолинейного проводника с током (рис. 80), имеем следующее: полный ток равен току в проводнике ∑I = I; контур, проведенный на расстоянии r от проводника, совпадает с магнитной линией; длина контура l будет l = 2πr, поэтому H ⋅ 2πl = I, откуда H = I/_2πr.

Переходя к магнитной индукции, будем иметь B = μ_aI/_2πr, т. е. мы получили то же выражение для магнитной индукции, которое было приведено выше Для такого же случая. Применим закон полного тока для определения напряженности поля по оси катушки, равномерно намотанной на кольцо (рис. 81). Контуром здесь является ось катушки (она же ось кольца). Площадь контура пронизывает полный ток, равный произведению тока I на число витков ω катушки, т. е. ∑I = Iω. Обозначив длину оси катушки через l, запишем закон полного тока:

H ⋅ l = Iω,

откуда

H = Iω/_l,

или, переходя к магнитной индукции, будем иметь

В = μ_аI⋅ω/_l.

Рис. 81. К определению напряженности поля катушки, намотанной на кольцо

Если сечение кольцевой катушки обозначить S, то магнитный поток, проходящий внутри катушки, будет

Φ = B ⋅ S = μ_aI⋅ω/_l S.

Разрезав кольцо и выпрямив катушку, мы получим соленоид. Для соленоида бесконечно большой длины формулы для напряжённости поля H по оси соленоида, магнитной индукции В и магнитного потока Φ те же, что и для кольцевой катушки. Однако на практике, имея дело с соленоидами ограниченной длины, для определения H, В и Φ пользуются теми же формулами.