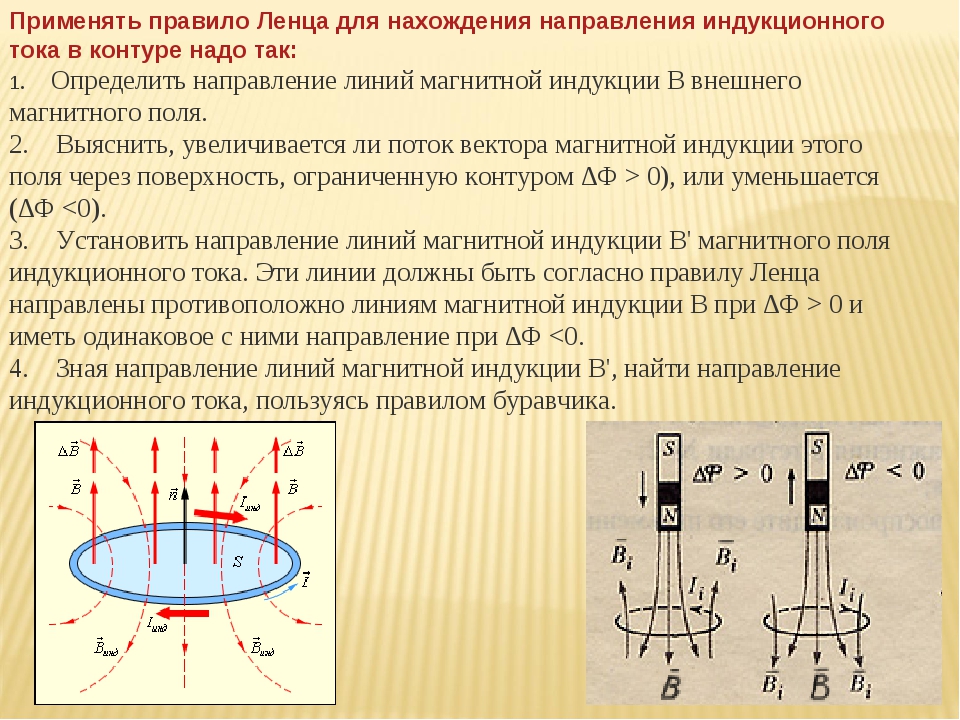
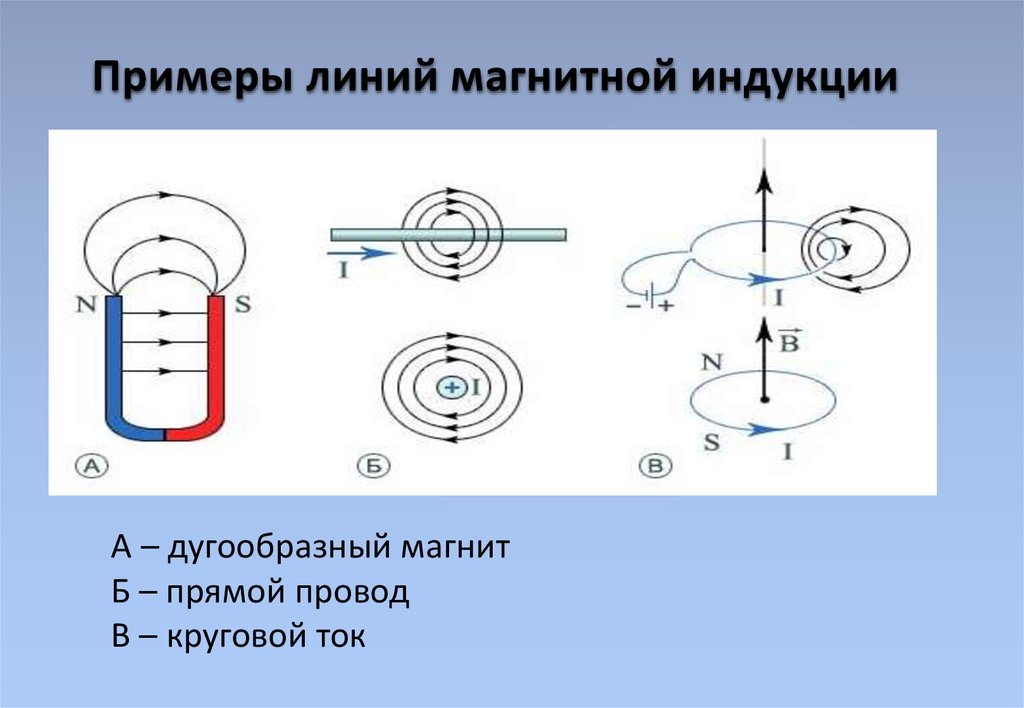
- Вихревое поле
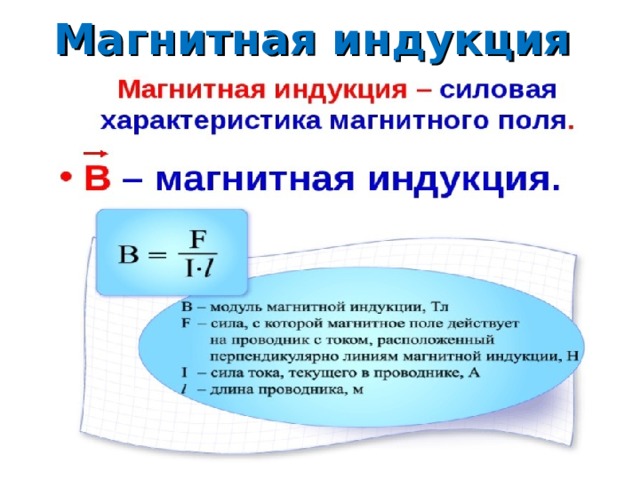
- Основные формулы для вычисления вектора МИ
- Закон Био-Савара-Лапласа
- Принцип суперпозиции
- Теорема о циркуляции
- Магнитный поток
- Основные уравнения
- В магнитостатике
- В общем случае
- Линии магнитной индукции
- Как возникает ЭДС индукции и индукционный ток?
- Сведения о линиях магнитной индукции
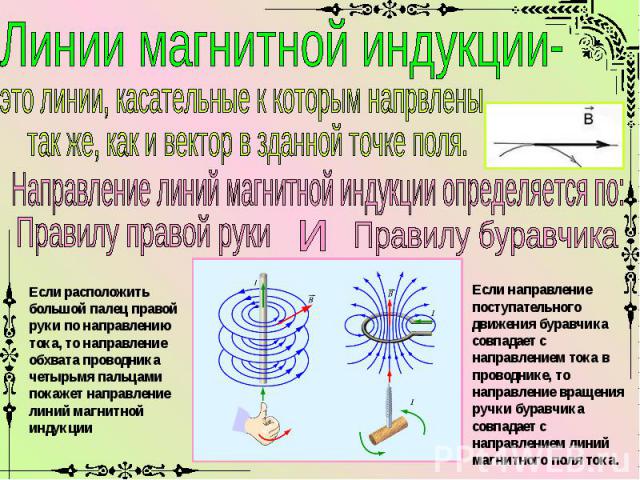
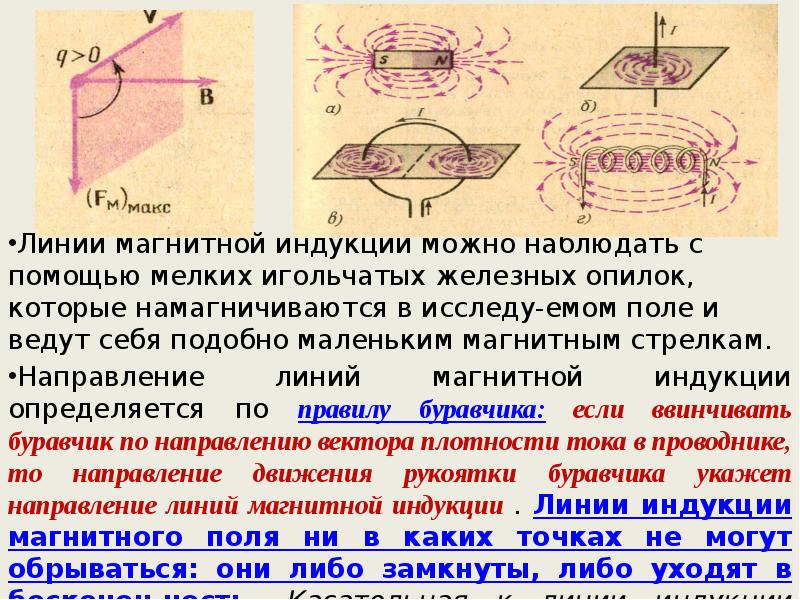
- Направление магнитной индукции
- Правило буравчика
- Правило обхвата правой рукой
- Что такое магнитный поток?
- Линии магнитной индукции
- Вихревое поле
- Непотенциальный характер магнитных сил
- Чему равно ЭДС индукции?
- Изображение линий магнитной индукции
- Что такое ЭДС самоидукции? Индуктивность
- Магнитное поле соленоида и тороида
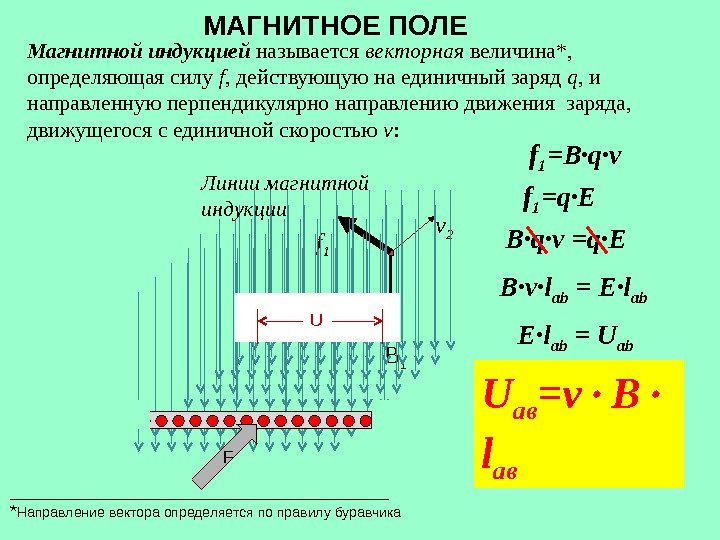
- Что такое магнитное поле?
- Примечания
- Источники магнитного поля
- Электромагнитное поле проводника
- Электромагнитная индукция
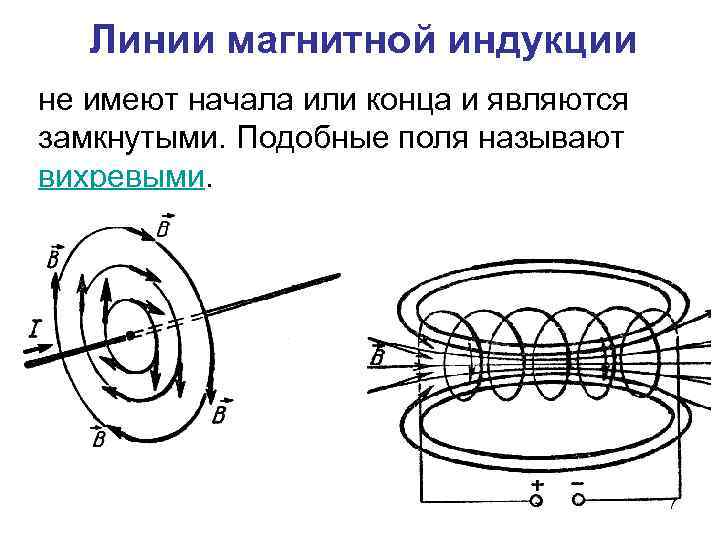
Вихревое поле
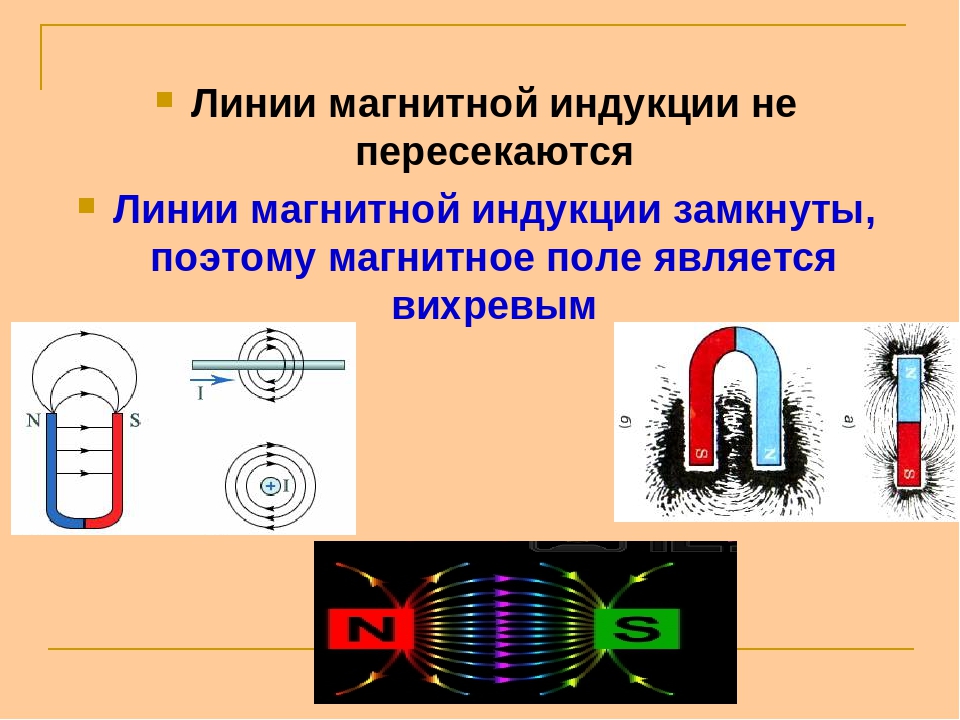
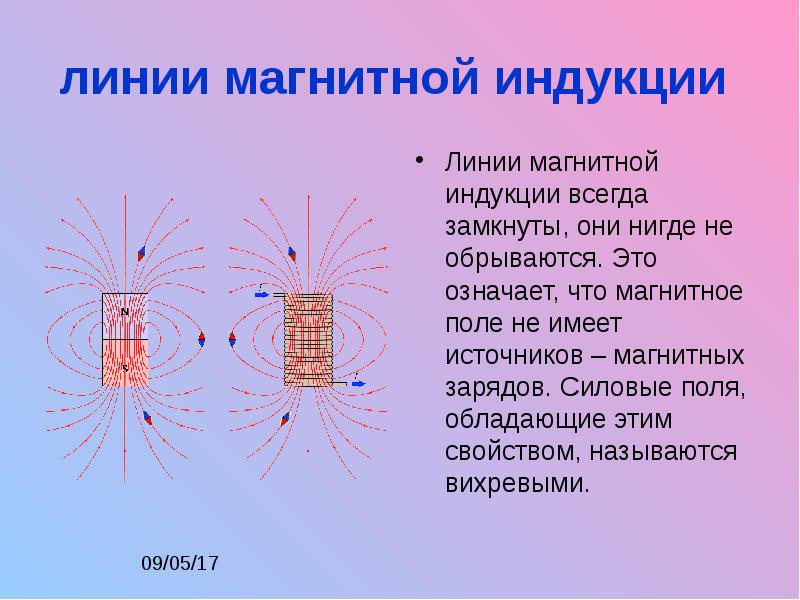
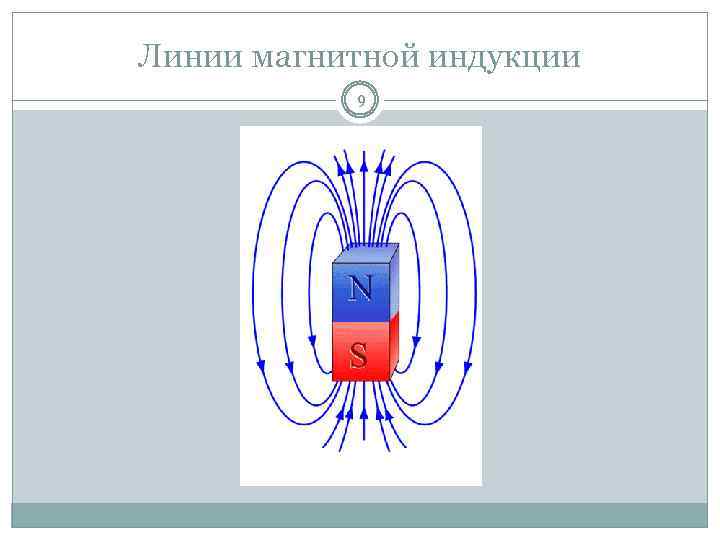
Внимательное исследование магнитного поля с помощью линий магнитной индукции позволяет установить очень важную его особенность. Линии магнитной индукции не имеют ни начала, ни конца. Они всегда замкнуты.
Вспомним, что с электростатическим полем дело обстоит иначе. Линии напряженности электростатического поля начинаются на положительных зарядах и оканчиваются на отрицательных.
Поля с замкнутыми силовыми линиями называются вихревыми. Магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобных электрическим, не обнаружено.
Заметим, что ни законы электродинамики, ни какие-либо другие известные физические законы не запрещают существования магнитных зарядов; точнее, существования частиц, обладающих магнитными зарядами. Поэтому предпринимались и предпринимаются поиски таких частиц. Однако они до сих пор не увенчались успехом. Причина этого пока не ясна.
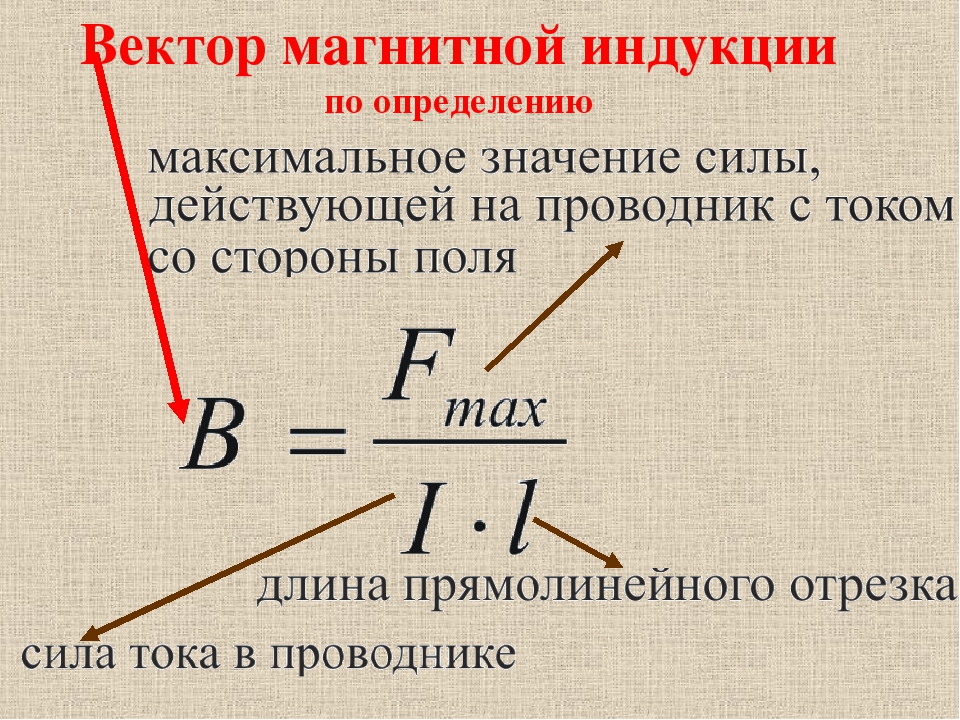
Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.
Закон Био-Савара-Лапласа
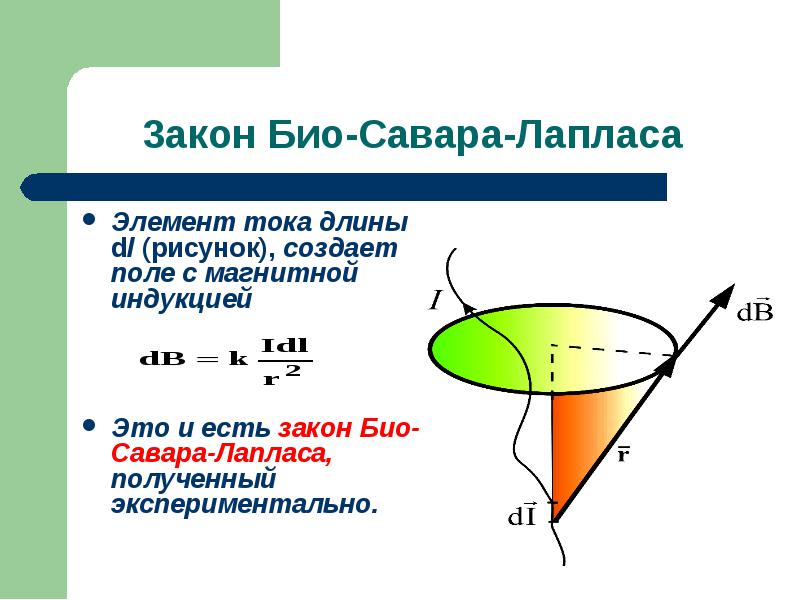
Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.
Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB
dB = µ0 *I*dl*sin α /4*π*r2,
где
- dB – магнитная индукция, Тл;
- µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
- I – сила тока, А;
- dl – отрезок проводника, м;
- r – расстояние до точки нахождения магнитной индукции, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме
 Закон Био-Савара-Лапласа
Закон Био-Савара-Лапласа
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого перемещения электронов;
- поля кругового движения заряженных частиц.
Формула для МП первого типа имеет вид:
В = µ* µ0*2*I/4*π*r.
Для кругового движения она выглядит так:
В = µ*µ0*I/4*π*r.
В этих формулах µ – это магнитная проницаемость среды (относительная).
Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:
B→= B1→+ B2→+ B3→… + Bn→
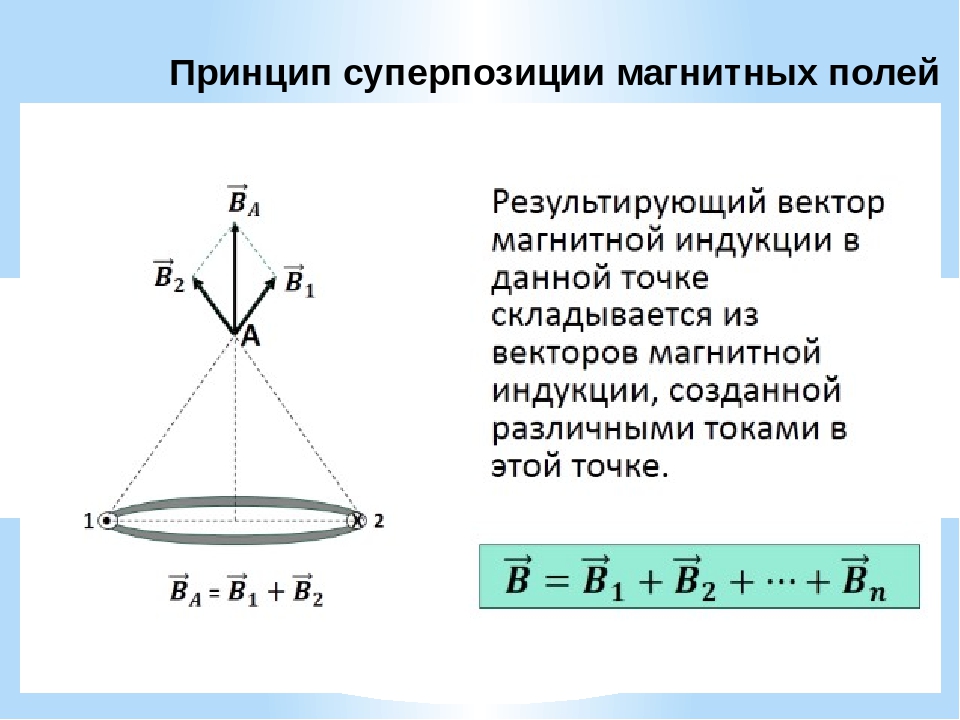 Принцип суперпозиции
Принцип суперпозиции
Теорема о циркуляции
Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.
Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.
Другое название теоремы – закон Ампера, описывающий циркуляцию МП.
Математически теорема записывается следующим образом.
 Математическая формула теоремы о циркуляции
Математическая формула теоремы о циркуляции
где:
- B→– вектор магнитной индукции;
- j→ – плотность движения электронов.
Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.
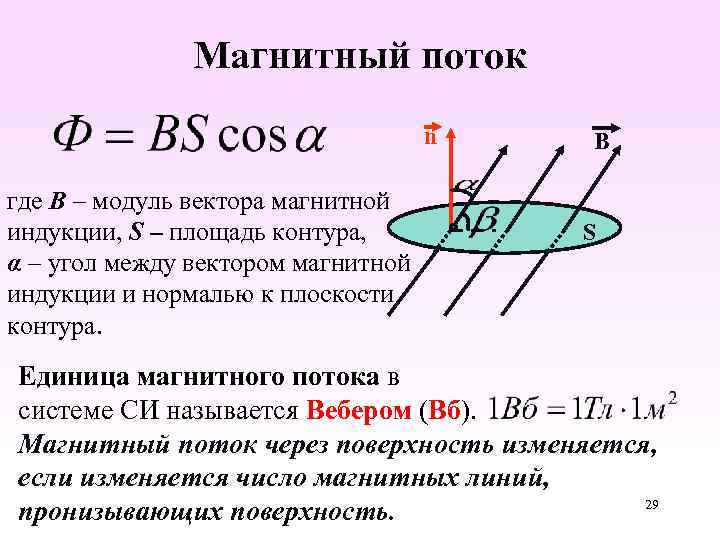
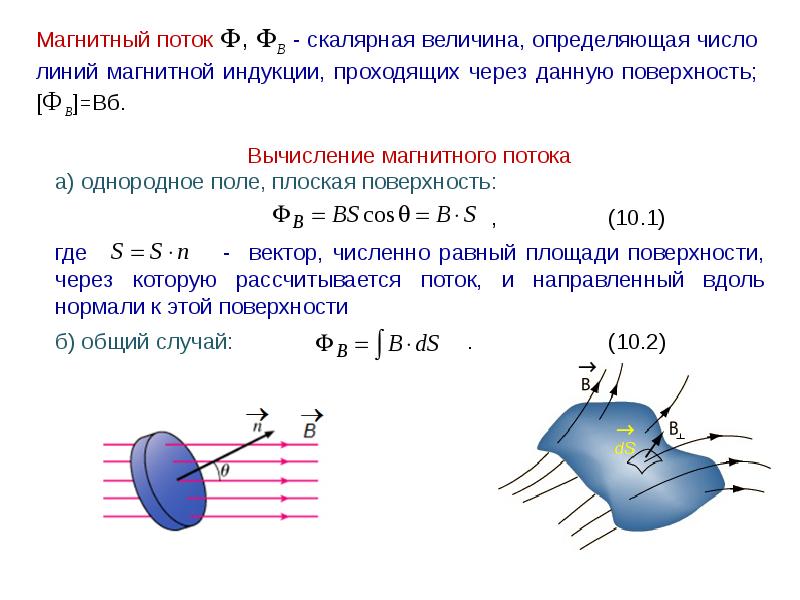
Магнитный поток
Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):
108 Мкс = 1 Вб.
Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.
Формула для расчёта имеет вид:
φ = |B*S| = B*S*cosα,
где
- В – скалярная величина градиента магнитной индукции;
- S – площадь пересекаемой поверхности;
- α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).
Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900)
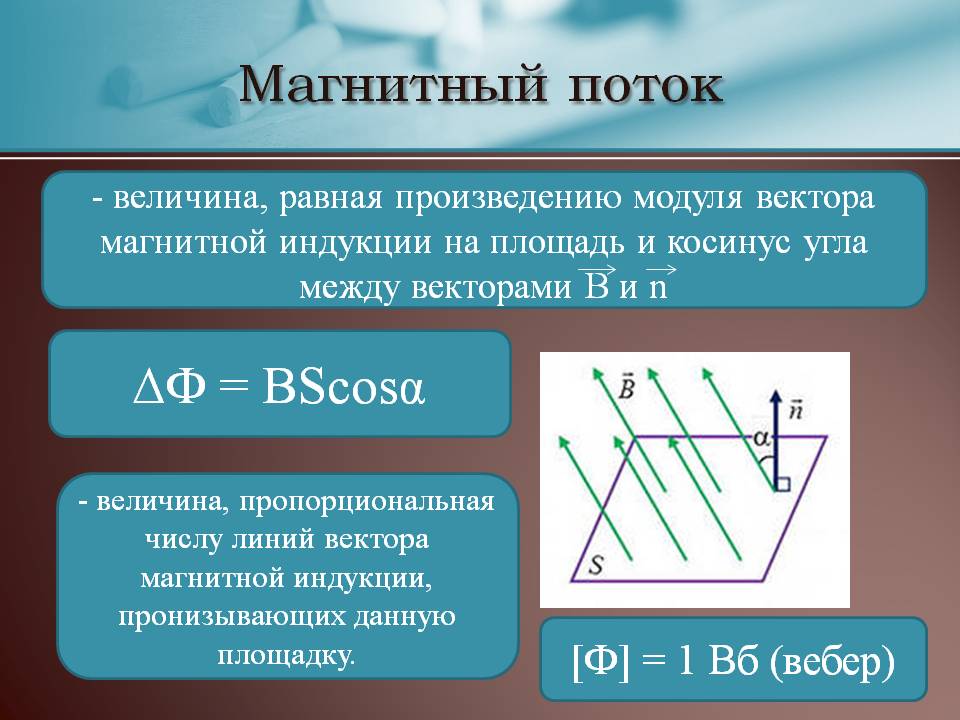 Магнитный поток
Магнитный поток
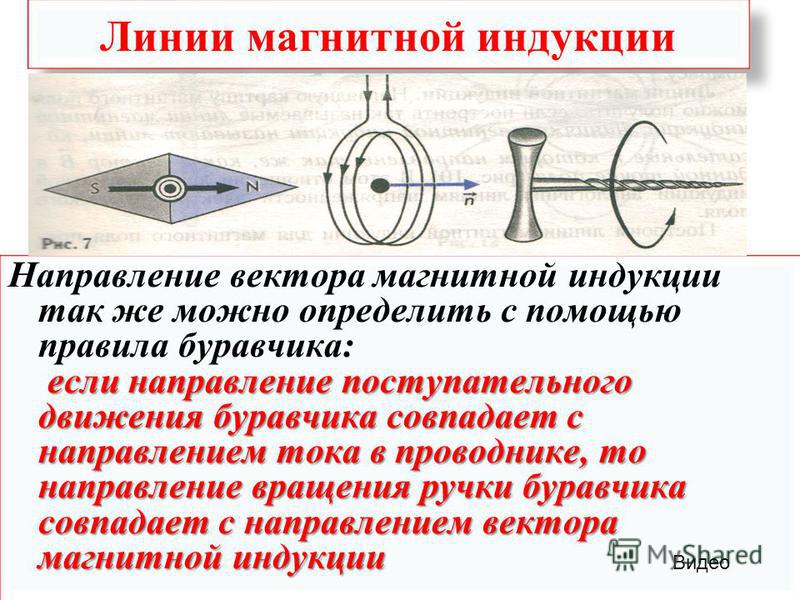
Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.
Основные уравнения
Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.
(Здесь формулы приведем в СИ, в виде для вакуума, где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).
В магнитостатике
В магнитостатическом пределе наиболее важными являются:
-
Закон Био — Савара — Лапласа: играет в магнитостатике ту же роль, что закон Кулона в электростатике:
- B→(r→)=μ4π∫L1I(r→1)dL1→×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int \limits _{L_{1}}{\frac {I\left({\vec {r}}_{1}\right){\vec {dL_{1}}}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}
- B→(r→)=μ4π∫j→(r→1)dV1×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int {\frac {{\vec {j}}\left({\vec {r}}_{1}\right)dV_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}
-
Теорема Ампера о циркуляции магнитного поля:
- ∮∂SB→⋅dl→=μIS≡μ∫Sj→⋅dS→,{\displaystyle \oint \limits _{\partial S}{\vec {B}}\cdot {\vec {dl}}=\mu _{0}I_{S}\equiv \mu _{0}\int \limits _{S}{\vec {j}}\cdot {\vec {dS}},}
- rotB→≡∇→×B→=μj→.{\displaystyle \mathrm {rot} \,{\vec {B}}\equiv {\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {j}}.}
В общем случае
Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции B→{\displaystyle {\vec {B}}}:
Три из четырех уравнений Максвелла (основных уравнений электродинамики)
-
- divE→=ρε, rotE→=−∂B→∂t{\displaystyle \mathrm {div} \,{\vec {E}}={\frac {\rho }{\varepsilon _{0}}},\ \ \ \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}}
- divB→=, rotB→=μj→+1c2∂E→∂t{\displaystyle \mathrm {div} \,{\vec {B}}=0,\ \ \ \ \,\mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}}
- а именно:
Закон отсутствия монополя:
-
- divB→=,{\displaystyle \mathrm {div} \,{\vec {B}}=0,}
Закон электромагнитной индукции Фарадея:
-
- rotE→=−∂B→∂t,{\displaystyle \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}
Закон Ампера — Максвелла:
-
- rotB→=μj→+1c2∂E→∂t.{\displaystyle \mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}.}
Формула силы Лоренца:
-
- F→=qE→+qv→×B→,{\displaystyle {\vec {F}}=q{\vec {E}}+q\left,}
-
- Следствия из неё, такие как
Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
-
- dF→=Idl→×B→,{\displaystyle d{\vec {F}}=\left,}
- dF→=j→dV×B→,{\displaystyle d{\vec {F}}=\left,}
выражение для момента силы, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):
-
- M→=m→×B→,{\displaystyle {\vec {M}}={\vec {m}}\times {\vec {B}},}
выражение для потенциальной энергии магнитного диполя в магнитном поле:
-
- U=−m→⋅B→,{\displaystyle U=-{\vec {m}}\cdot {\vec {B}},}
- а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
- Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
-
- F→=Kqmr→r3.{\displaystyle {\vec {F}}=K{\frac {q_{m}{\vec {r}}}{r^{3}}}.}
(это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).
Выражение для плотности энергии магнитного поля
-
- w=B22μ{\displaystyle w={\frac {B^{2}}{2\mu _{0}}}}
Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).
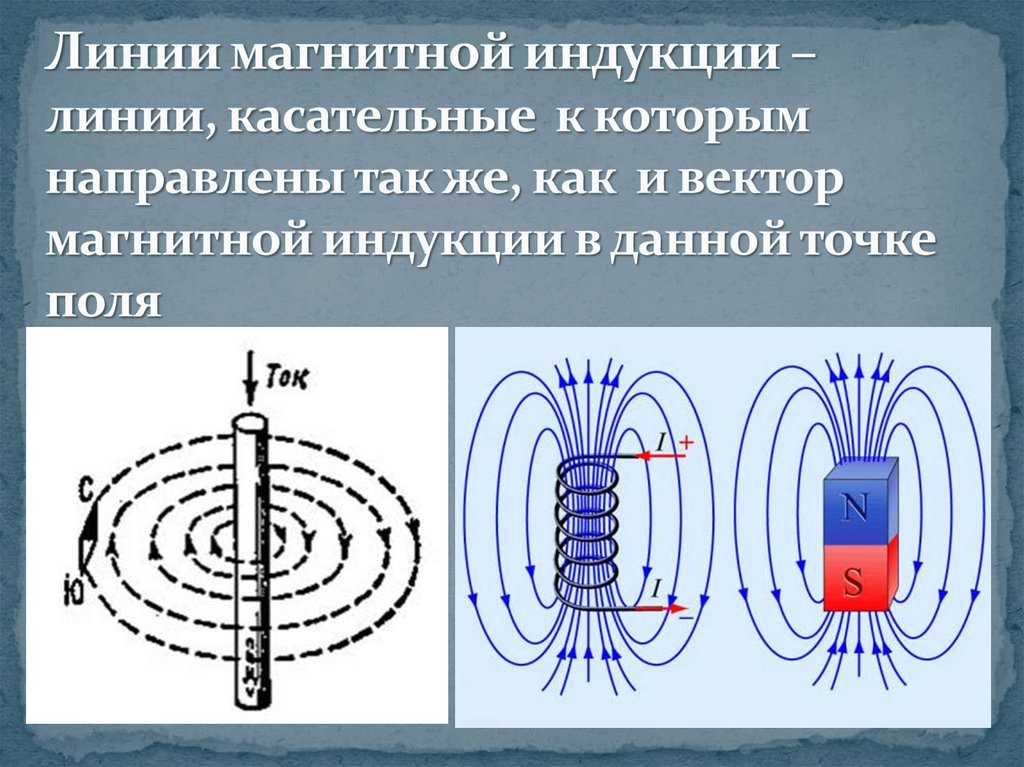
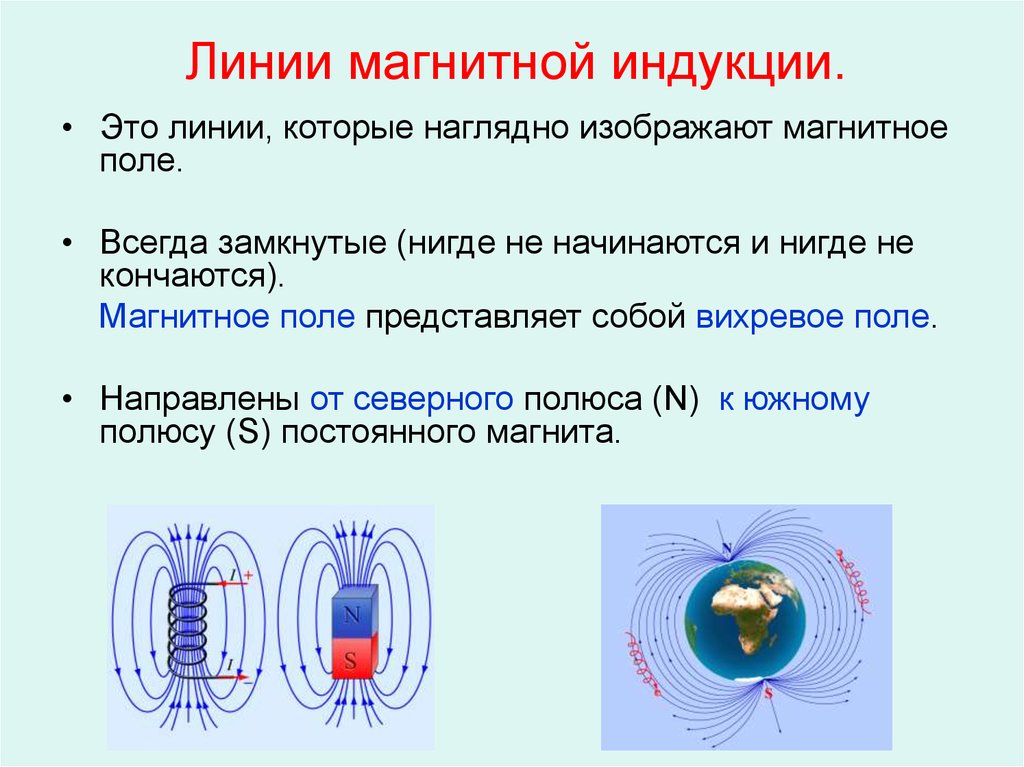
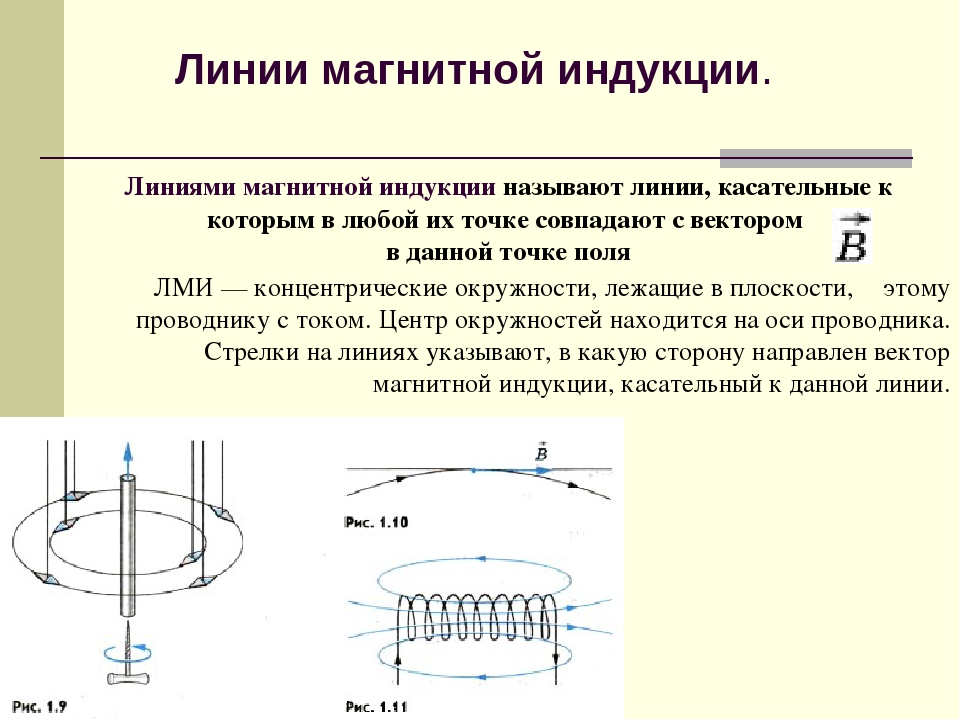
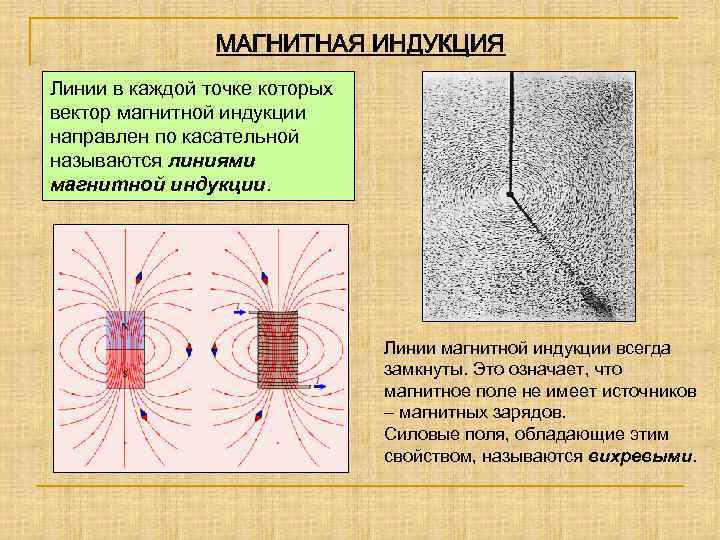
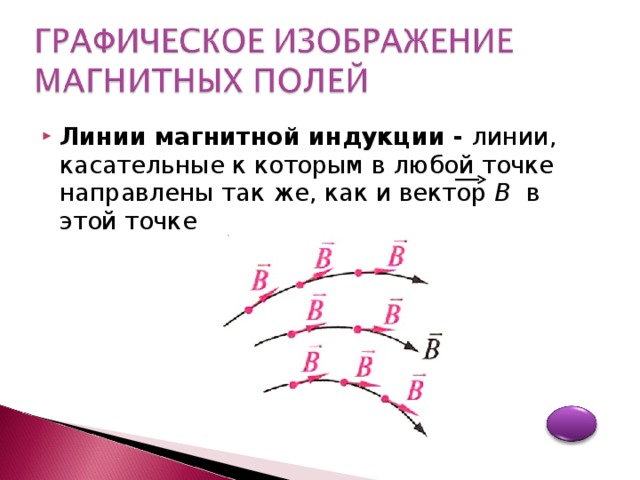
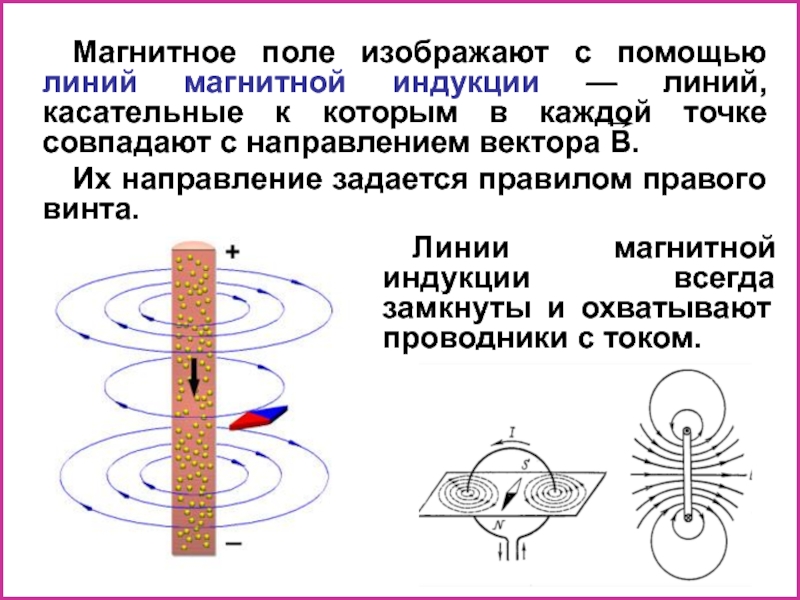
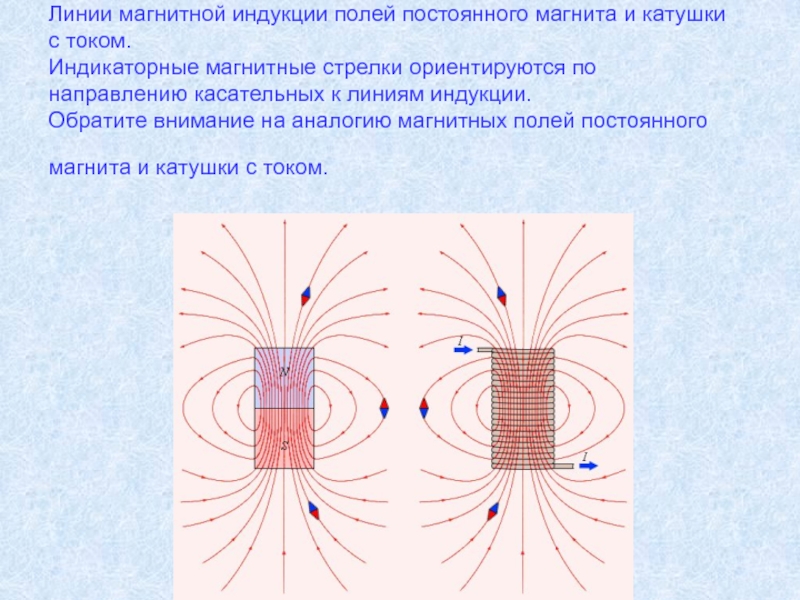
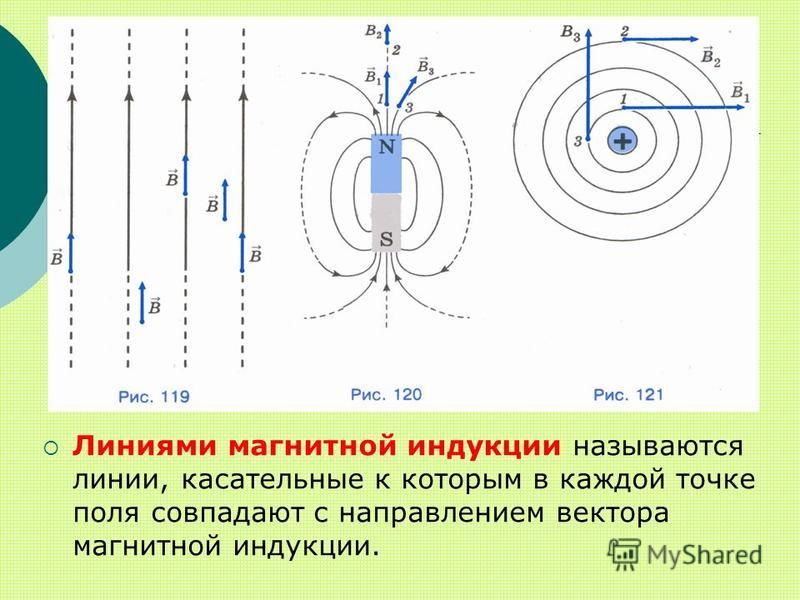
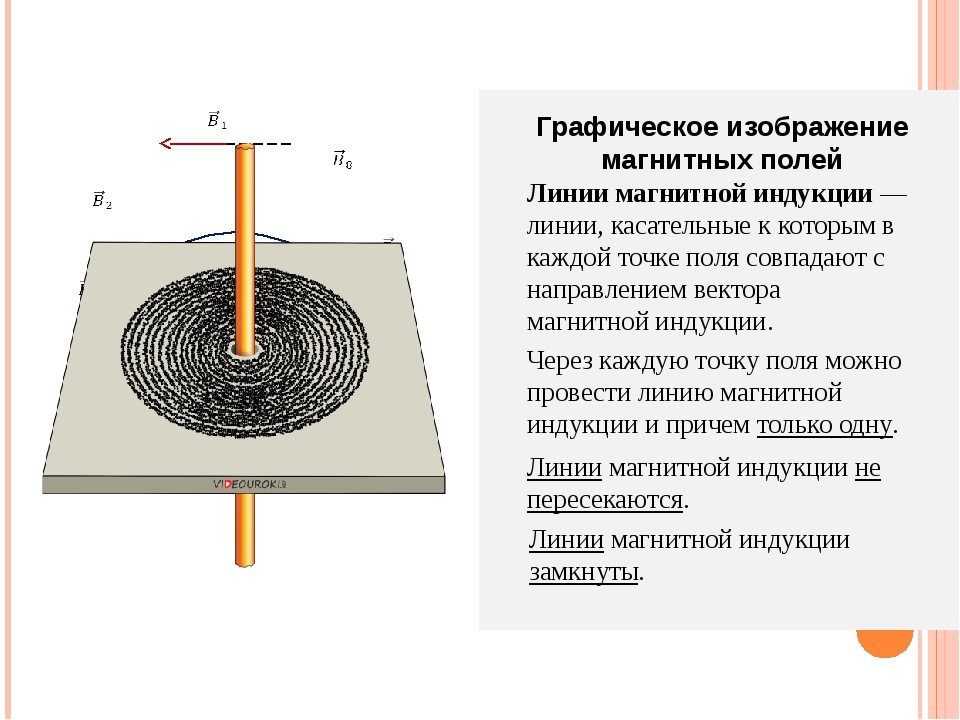
Линии магнитной индукции
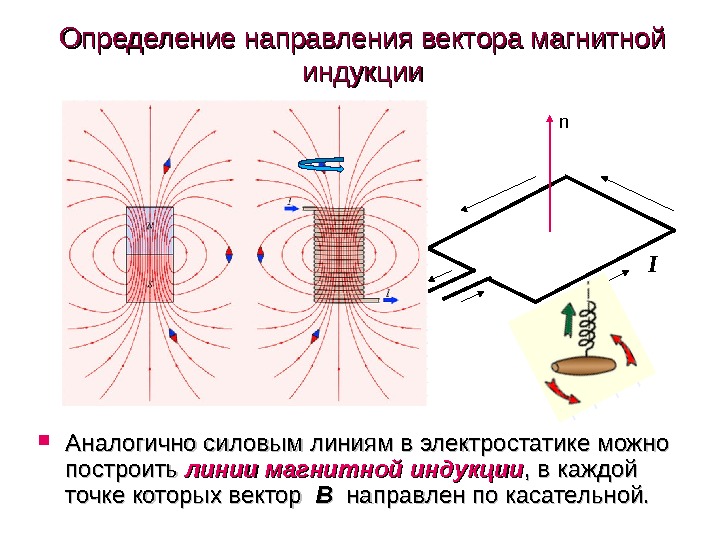
Линиями магнитной индукции называются линии, касательные к которым направлены так же, как и вектор в данной точке пространства (рис. 4.22).
Построим линии магнитной индукции для магнитного поля прямолинейного проводника с током. Из приведенных ранее описаний опытов с контуром и магнитной стрелкой, а также из соображений симметрии следует, что линии магнитной индукции в данном случае — концентрические окружности, лежащие в плоскости, перпендикулярной этому проводнику с током. Центр окружностей находится на оси проводника (рис. 4.23). Как и в случае линий напряженности электрического поля, линии магнитной индукции можно условиться проводить так, чтобы их густота характеризовала модуль вектора В в данном месте. На рисунке 4.23 концентрические окружности сгущаются к центру. Это должно означать, что магнитная индукция вблизи провода больше, чем вдали от него.
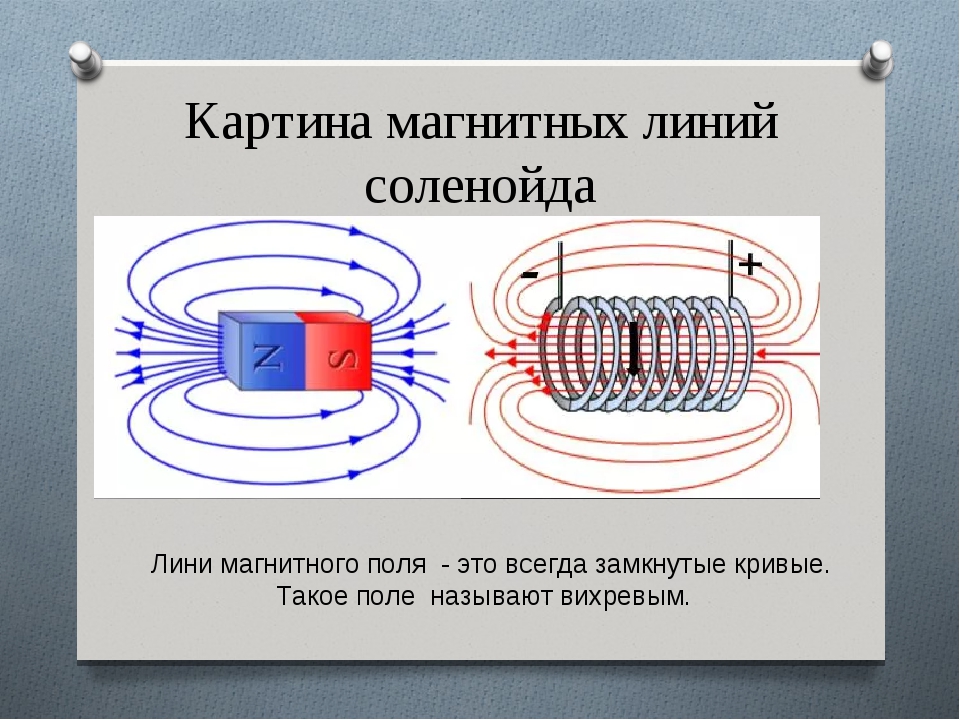
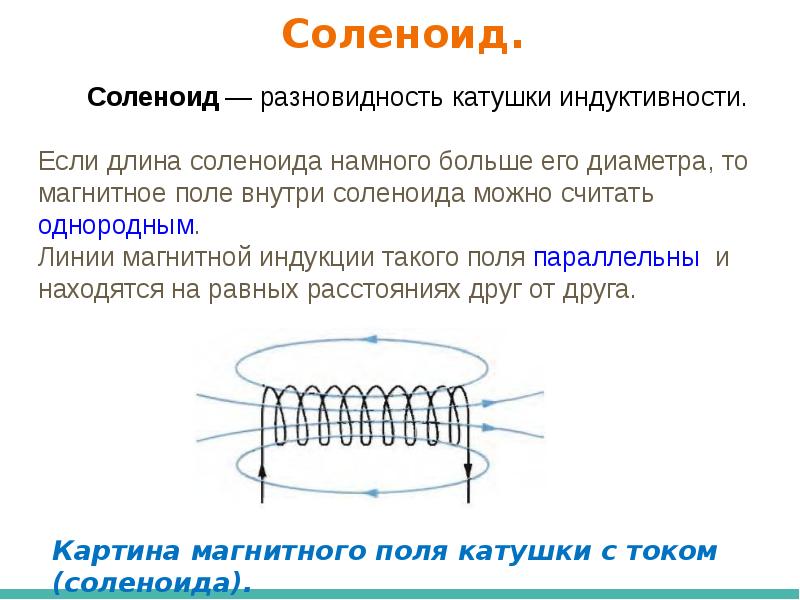
Картина линий магнитной индукции катушки с током (соленоида) показана на рисунке 4.24 (соленоид дан в разрезе). Если длина соленоида много больше его диаметра, то поле внутри соленоида можно считать однородным. Линии магнитной индукции такого поля параллельны, их густота везде одинакова.

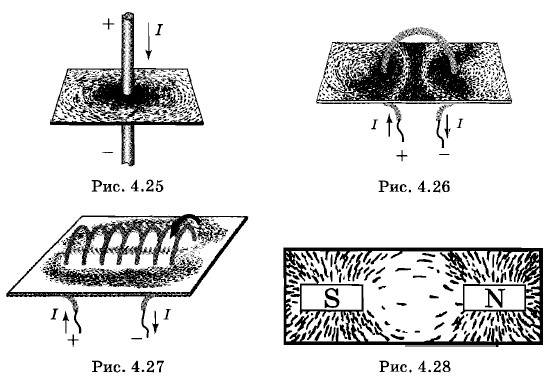
Картину линий магнитной индукции можно сделать видимой, воспользовавшись мелкими железными опилками. В магнитном поле каждый из насыпанных на лист картона кусочков железа намагничивается и ведет себя как маленькая магнитная стрелка. Наличие такого большого количества стрелок позволяет в большом числе точек определить направление вектора магнитной индукции магнитного поля и, следовательно, более точно выяснить расположение линий индукции. Некоторые из картин магнитного поля приведены на рисунках 4.25—4.28.
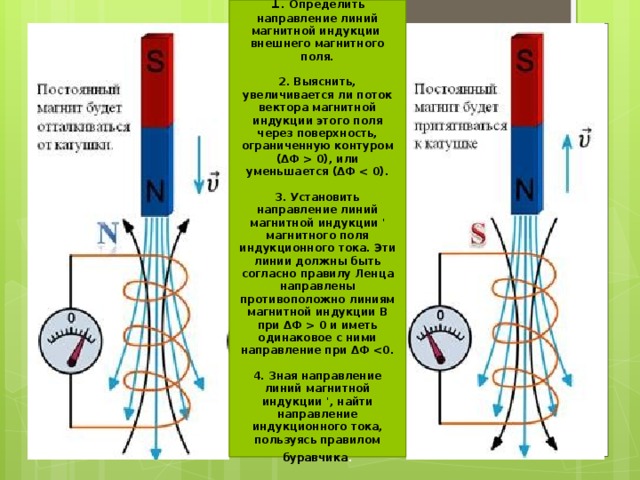
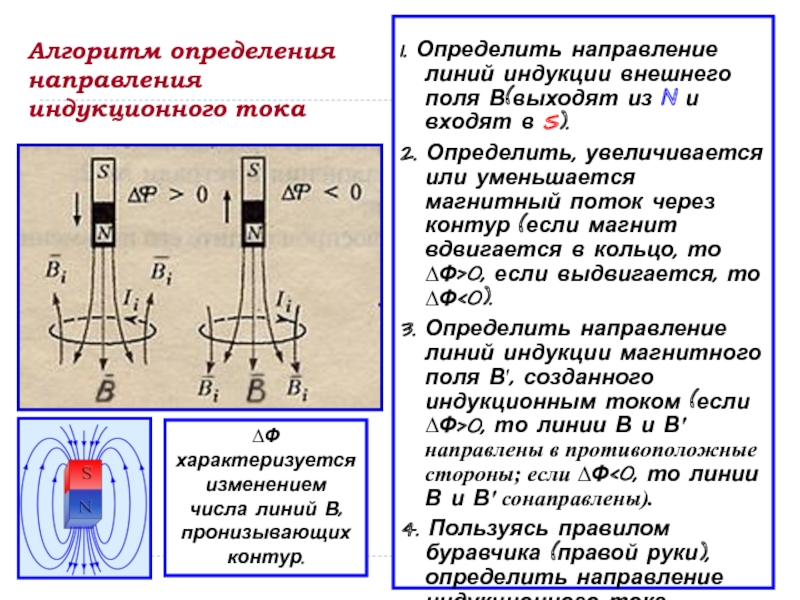
Как возникает ЭДС индукции и индукционный ток?
Как я говорил в предыдущих статьях вокруг проводника, по которому протекает электрический ток, возникает электромагнитное поле. Данное магнитное поле я рассмотрел здесь и здесь. Однако существует и обратное явление, которое называется электромагнитная индукция. Данное явление открыл английский физик М. Фарадей.
Для рассмотрения данного явления рассмотрим следующий рисунок

На данном рисунке показана рамка из проводника, помещённая в электрическое поле с индукцией В. Если данную рамку двигать вверх-вниз по направлению магнитных силовых линий или влево – вправо перпендикулярно силовым линиям, то магнитный поток Φ пронизывающий рамку буден практически постоянным. Если же вращать рамку вокруг оси О, то за некоторый промежуток времени ∆t магнитный поток изменится на некоторую величину ∆Φ и в результате в рамке появится ЭДС индукции Еi и потечёт ток I, называемым индукционным током.
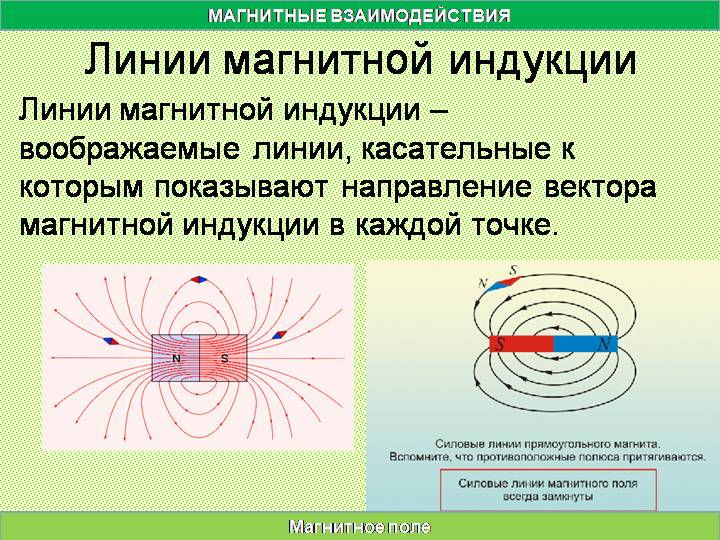
Сведения о линиях магнитной индукции
Из приведенных данных понятна силовая природа поля, созданного переменным током или перемещением проводника. Векторное выражение используют для точного выражения воздействий на индикаторный элемент. В начале публикации таким компонентом была стрелка компаса. Далее показана возможность применения проводящей рамки с током.
Линии индукции магнитного поля применяют для наглядного изображения данного явления. Если в любой точке такой кривой нарисовать вектор (В) по касательной, он укажет направление воздействия. Размером в масштабе показывают определенную силу.
Элементарной проверкой геометрических параметров можно установить уникальность каждого вектора. Они, как и линии силового поля, не пересекаются. Ниже представлены способы для уточнения распределения энергетических потоков в проводнике и окружающем пространстве.
 Два способа определения направленности силового поля (электрического тока)
Два способа определения направленности силового поля (электрического тока)
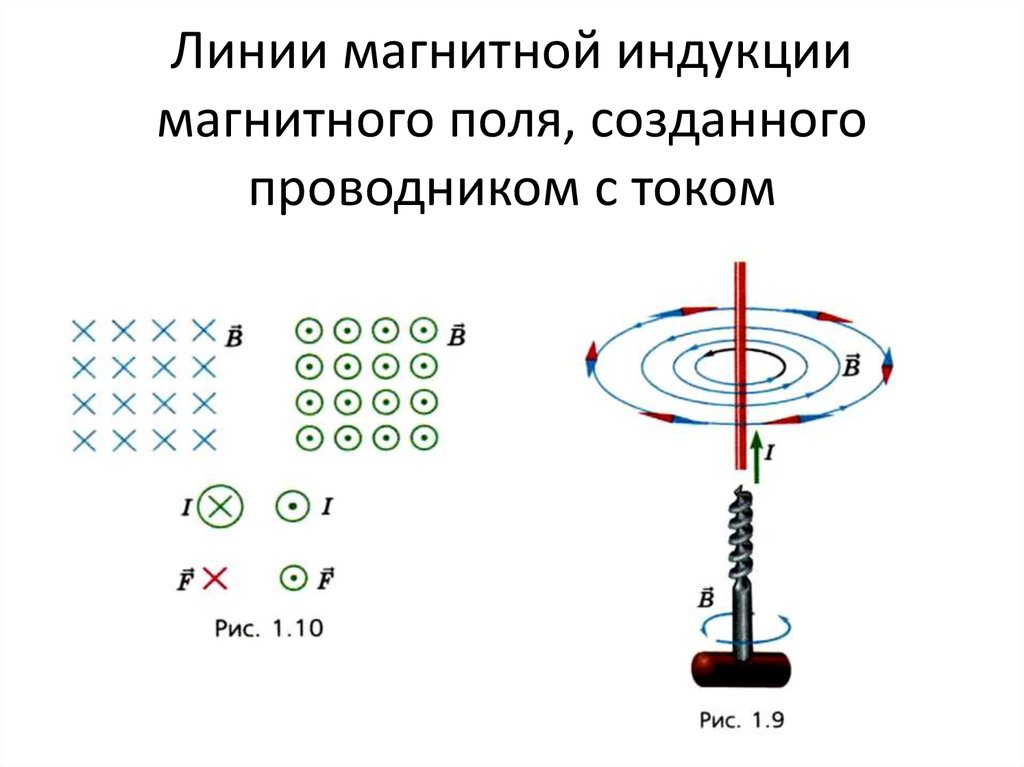
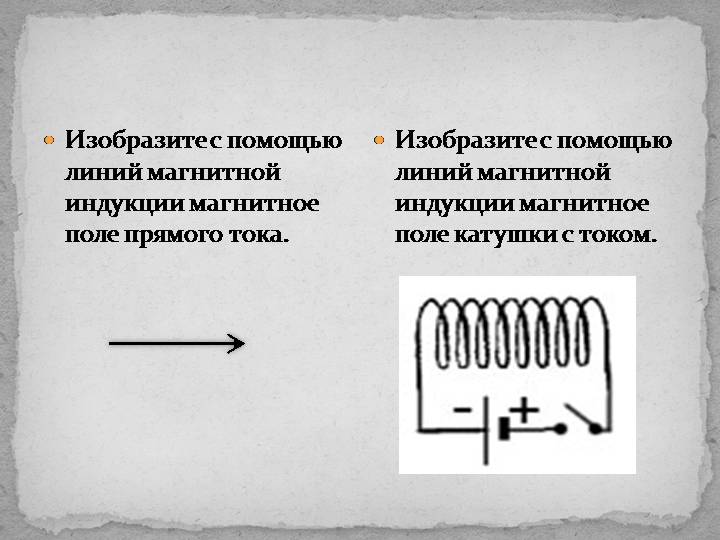
Для варианта с прямолинейным проводником правую руку сжимают, как показано на первом рисунке. Большой палец направляют в сторону движения тока. Сжатые пальцы покажут направление силовых линий. Вторая часть картинки демонстрирует определение параметров поля при пропускании тока через кольцевую рамку – «правило буравчика». Вращение этого инструмента аналогично направлению тока.
К сведению. Если соленоид достаточно большой по длине, поле в большей части рабочего объема будет однородным. Допустимо считать, что линии магнитного поля в этом случае расположены параллельно.
Направление магнитной индукции
Магнитные силы, как и любые другие силы, имеют направление. Для его определения служат специальные правила.
Правило буравчика
Согласно этому правилу, если направление поступательного движения острия буравчика при ввинчивании совпадает с направлением тока в проводнике, то направление вращательного движения буравчика в каждой точке совпадает с направлением вектора индукции магнитного поля.
Рис. 2. Правило буравчика.
Правило обхвата правой рукой
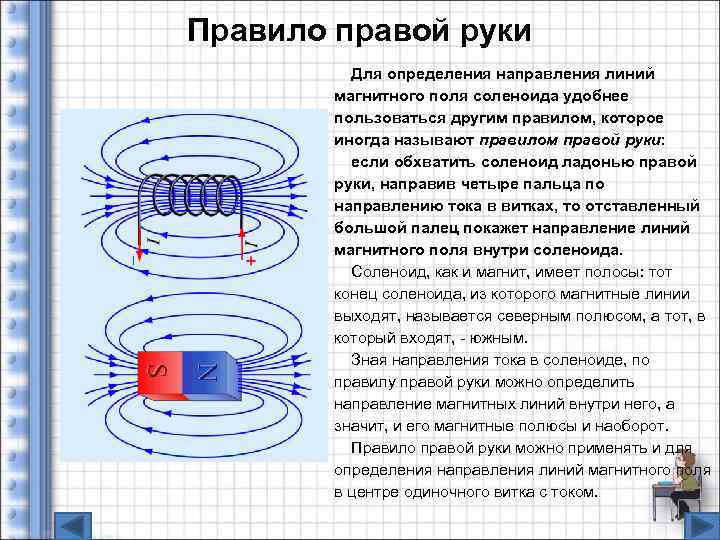
Приведенное правило зачастую недостаточно понятно из-за того, что буравчик в современном мире используется нечасто. Поэтому гораздо удобнее применять правило охвата правой рукой: если большой палец правой руки указывает направление тока, то остальные пальцы будут показывать направление магнитных линий.
Данное правило удобнее еще и потому, что его можно применять и для определения направления магнитной индукции катушки с током, в этом случае четыре пальца направляются вдоль витков катушки, в направлении тока в них, а большой палец укажет направление вектора магнитной индукции. То есть, большой палец в обоих случаях указывает на прямую линию, а остальные пальцы – на охватывающую.
Рис. 3. Правило обхвата правой рукой.
Что такое магнитный поток?
Магнитным потоком называется физическая величина пропорциональная количеству силовых линий магнитного поля на определённой площади пространства. Так как силовые линии являются абстрактным понятием, то, следовательно, магнитный поток характеризует интенсивность магнитного поля, то есть магнитную индукцию на данной площади. Магнитный поток обозначается Ф и имеет размерность Вб (Вебер).
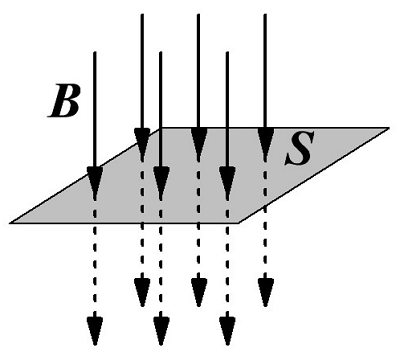
Таким образом, магнитный поток можно выразить следующим выражением
где В – магнитная индукция,
S – площадь поверхности, для которой рассчитывается магнитный поток.
На рисунке изображены силовые линии магнитного поля, которые перпендикулярны к поверхности S, то есть угол между вектором магнитной индукции В и поверхностью S равен 90°. Однако часто бывает, что необходимо вычислит магнитный поток на плоскости не перпендикулярной вектору магнитной индукции. Для определения такого магнитного потока необходимо привести вектор магнитной индукции к нормали
Таким образом, итоговое выражение для нахождения магнитного потока будет иметь вид
где В – вектор магнитной индукции,
S – площадь поверхности, на которой находят магнитный поток,
α – угол между вектором магнитной индукции и нормалью к поверхности S.
Линии магнитной индукции
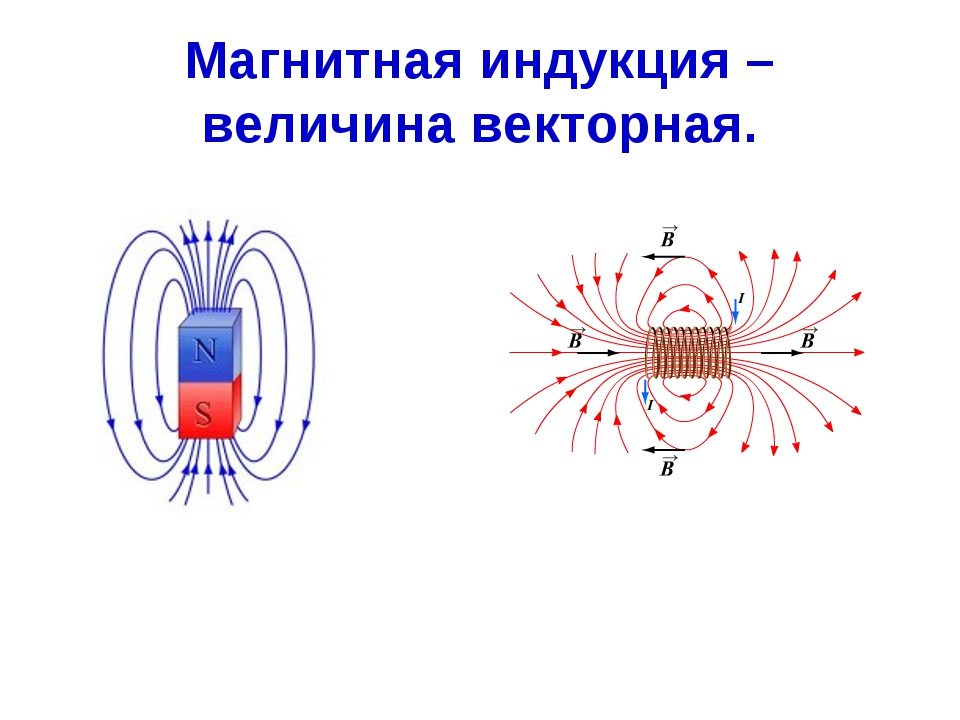
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым в любой их точке совпадают с вектором в данной точке поля (рис. 1.10). Линии вектора магнитной индукции аналогичны линиям вектора напряженности электростатического поля.
Для магнитного поля прямолинейного проводника с током из приведенных ранее опытов следует, что линии магнитной индукции — концентрические окружности, лежащие в плоскости, перпендикулярной этому проводнику с током (см. рис. 1.9). Центр окружностей находится на оси проводника. Стрелки на линиях указывают, в какую сторону направлен вектор магнитной индукции, касательный к данной линии.
На рисунке 1.11 показана картина магнитного поля катушки с током (соленоида). Если длина соленоида много больше его диаметра, то магнитное поле внутри соленоида можно считать однородным. Линии магнитной индукции такого поля параллельны и находятся на равных расстояниях друг от друга.
На рисунке 1.12 показано магнитное поле Земли. Линии магнитной индукции поля Земли подобны линиям магнитной индукции поля соленоида. Магнитный северный полюс N близок к Южному географическому полюсу, а магнитный южный полюс S — к Северному географическому полюсу. Ось такого большого магнита составляет с осью вращения Земли угол 11,5°. Периодически магнитные полюсы меняют свою полярность. Последняя такая замена произошла около 30 000 лет назад.
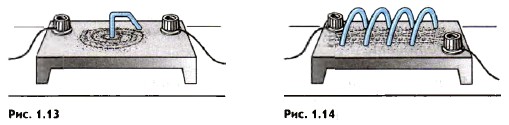
Картину линий магнитной индукции можно сделать видимой, воспользовавшись мелкими железными опилками. С этим методом вы уже знакомы.
В магнитном поле каждый кусочек железа, насыпанный на лист картона, намагничивается и ведет себя как маленькая магнитная стрелка. Большое количество таких стрелок позволяет в большем числе точек определить направление магнитного поля и, следовательно, точнее выяснить расположение линий магнитной индукции. Примеры картин магнитного поля приведены на рисунках 1.13—1.16.
Вихревое поле
Поля с замкнутыми векторными линиями называют вихревыми. Магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобных электрическим, в природе не существует.
Магнитное поле — вихревое поле, в каждой точке поля вектор магнитной индукции имеет определенное направление. Это направление указывает магнитная стрелка или его можно определить по правилу буравчика. Магнитное поле не имеет источников; магнитных зарядов в природе не существует.
Вопросы к параграфу
1. Как ориентируются в однородном магнитном поле замкнутый контур с током и магнитная стрелка?
2. Что называют линиями магнитной индукции?
3. Какие поля называют вихревыми?
4. Чем вихревое поле отличается от потенциального?
Непотенциальный характер магнитных сил
Замкнутость силовых линий магнитного поля означает, что работа магнитных сил на замкнутом пути может быть не равна нулю. Магнитные силы, в отличие от электростатических, непотенциальны.
Непотенциальный характер магнитных сил отчетливо проявляется во вращении проводника с током в поле постоянного магнита. Впервые подобное вращение (прообраз современного электродвигателя) осуществил Фарадей через год после открытия Эрстеда.
Концы подвешенного П-образного проводника Фарадей опустил в желоб со ртутью. Снизу через желоб проходил вертикально магнит так, что один из его полюсов выступал над ртутью.
Благодаря этому проводники с током находились в магнитном поле одного полюса магнита. При пропускании тока через ртуть и проводник последний начинал вращаться вокруг магнита. На рисунке 4.29 изображена действующая модель установки Фарадея.
Этот опыт демонстрирует еще одно замечательное свойство магнитных взаимодействий — его нецентральный характер. Полюс магнита не притягивает и не отталкивает проводники с током, а заставляет их поворачиваться вокруг себя. Сила, действующая со стороны магнита, не направлена вдоль линии, соединяющей полюс магнита с отдельными участками проводника с током.
Чему равно ЭДС индукции?
Для определения величины возникающей ЭДС рассмотрим контур помещенный в однородное магнитное поле с индукцией В, по данному контуру свободно может перемещаться проводник длиной l.
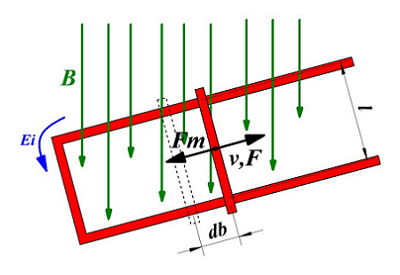
Под действием силы F проводник начинает двигаться со скоростью v. За некоторое время ∆t проводник пройдёт путь db. Таким образом, затрачиваемая работа на перемещение проводника составит
Так как проводник состоит из заряженных частиц – электронов и протонов, то они также движутся вместе с проводником. Как известно на движущуюся заряженную частицу действует сила Лоренца, которая перпендикулярна к направлению движения частицы и к вектору магнитной индукции В, то есть электроны начинают двигаться вдоль проводника приводя к возникновению электрического тока в нём.
Однако на проводник с током в магнитном поле действует некоторая сила Fт, которая в соответствии с правилом левой руки будет противоположна действию силы F, за счёт которой проводник движется. Так как проводник движется равномерно, то есть с постоянной скоростью, то силы Fт и F равны по абсолютному значению
где В – индукция магнитного поля,
I – сила тока в проводника, возникающая по действием ЭДС индукции,
l – длина проводника.
Так как путь db пройденный проводником зависит от скорости v и времени t, то работа, затрачиваемая на перемещения проводника, в магнитном поле составит
При перемещении проводника в магнитном поле практически вся затрачиваемая на эту работу механическая энергия переходит в электрическую энергию, то есть
Таким образом, преобразовав последнее выражение, получим значение ЭДС индукции при движении прямолинейного проводника в магнитном поле
где В – индукция магнитного поля,
l – длина проводника,
v – скорость перемещения проводника.
Данное выражение соответствует движению проводника перпендикулярно линиям магнитной индукции. Если происходит движение под некоторым углом к линиям магнитной индукции, то выражение приобретает вид
На практике достаточно трудно посчитать скорость перемещения проводника, поэтому преобразуем выражение к следующему виду
где dS – площадка, которую пересекает проводник при своём движении,
dΦ – магнитный поток пронизывающий площадку dS.
Таким образом, ЭДС индукции равна скорости изменения магнитного потока, который пронизывает контур.
Для обозначения направления движения тока в контуре вводят знак «–», который указывает, что ток в контуре направлен против положительного обхода контура. Таким образом
Зачастую в магнитном поле движется контур, состоящий из множества витков провода, поэтому ЭДС индукции будет иметь вид
где w – количество витков в контуре,
dΨ = wdΦ – элементарное потокосцепление.
Перефразируя предыдущее определение, ЭДС индукции в контуре равна скорости изменения потокосцепления этого контура.
Изображение линий магнитной индукции
Чтобы наглядно изучить распределение поля в пространстве, уменьшают размеры измерительных элементов. Для эксперимента подойдут железные опилки, равномерно рассыпанные на поверхности картонного листа или другой электрически нейтральной плоскости.
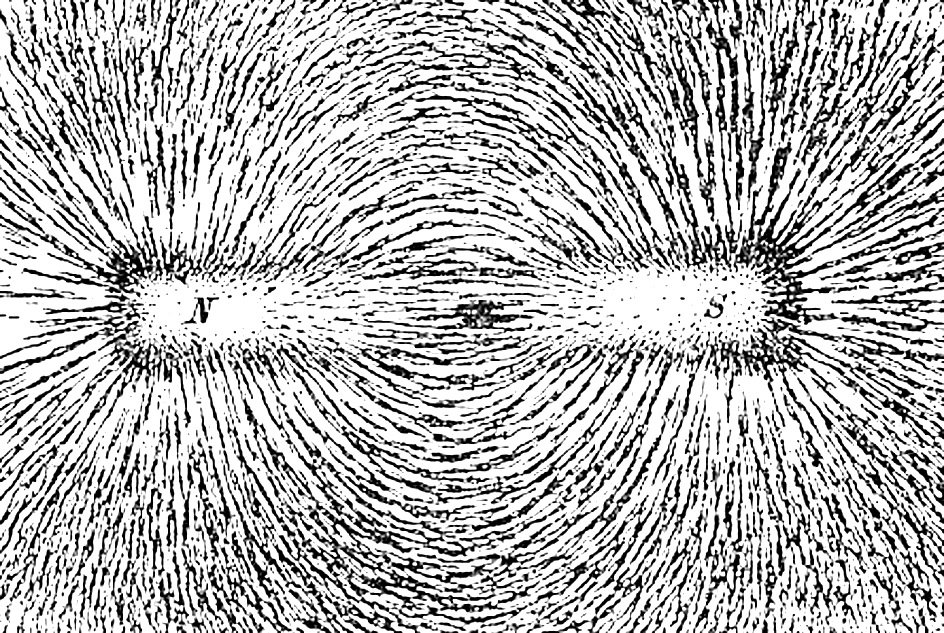 Линии магнитной индукции – наглядное изображение распределения силового поля
Линии магнитной индукции – наглядное изображение распределения силового поля
Если поднести с обратной стороны магнит, металлические частицы, как миниатюрные стрелки компаса, распределяться вдоль силовых полос. По расстоянию между ними можно судить об энергетических параметрах поля в определенном месте. Аналогичным образом создают рисунок. Большая густота (около полюсов) свидетельствует об увеличенном значении индукции.
К сведению. Физическим разделением постоянного магнита на части не получится создать отдельные полюса. В этом – принципиальное отличие от электростатических зарядов определенной полярности, которые также создают силовое поле.
Представленные знания применяют для решения разных инженерных задач. В частности, пригодятся простые правила определения направления тока в проводнике и стороны, в которую перемещается сердечник соленоида.
 Поезд на магнитной подушке разгоняется до высоких скоростей с минимальными энергетическими потерями
Поезд на магнитной подушке разгоняется до высоких скоростей с минимальными энергетическими потерями
Что такое ЭДС самоидукции? Индуктивность
Как известно вокруг проводника с током существует магнитное поле. Так как индукция магнитного поля пропорциональна силе тока протекающего через проводник, а магнитный поток пропорционален магнитной индукции, следовательно, магнитный поток пропорционален силе тока, протекающей через проводник.
Таким образом, при изменении силы тока происходит изменение магнитного потока (или потокосцепления). Однако в соответствие с законом электромагнитной индукции, изменение потокосцепления приводит к возникновению в проводнике ЭДС индукции.
Данное явление (возникновение ЭДС) в проводнике при изменении проходящего по нему тока называется самоиндукцией. Возникающая вследствие самоиндукции ЭДС называется ЭДС самоиндукции ЕL, которая равна
где dΨL – изменение потокосцепления.
Следовательно между электрическим током в проводнике и потокосцеплением, возникающего вокруг проводника магнитного поля существует некоторый коэффициент пропорциональности связывающий их. Таким коэффициентом является индуктивность – обозначается L (имеет старое название коэффициент самоиндукции)
Величина индуктивности характеризует способность электрической цепи создавать потокосцепление (магнитный поток) при протекании по ней электрического тока. Единицей индуктивности является Генри (обозначается Гн)
Таким образом, индуктивность зависит от геометрических размеров проводника с током и от магнитных свойств магнитной цепи, через которую замыкается магнитный поток, создаваемый проводником с током.
В следующей статье я расскажу, как рассчитать индуктивность различных по форме проводников с током.
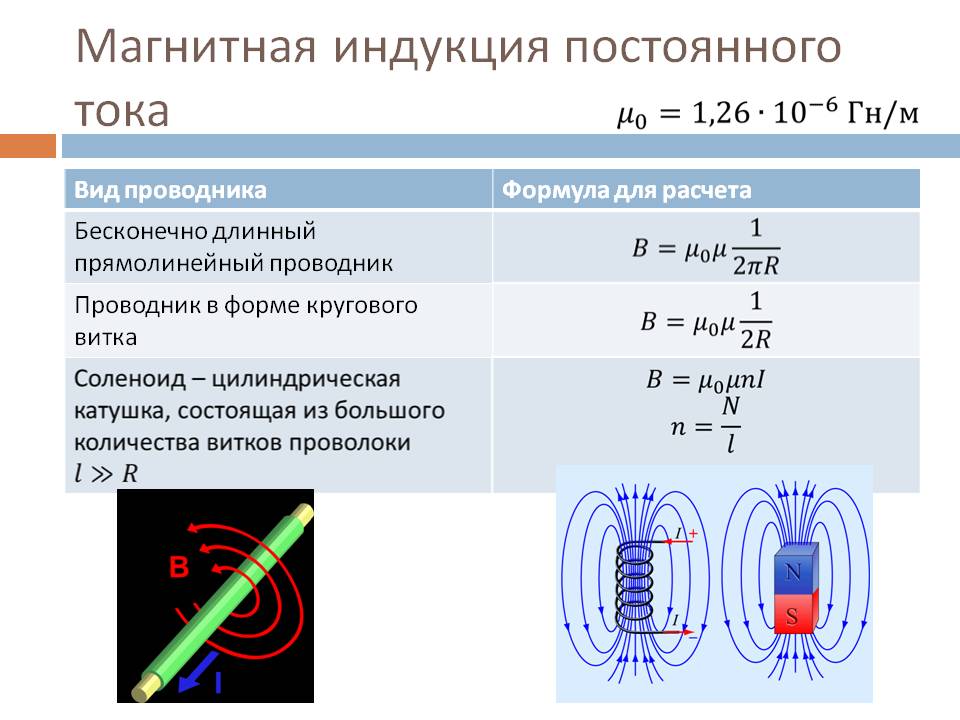
Магнитное поле соленоида и тороида
С помощью закона полного тока и циркуляции вектора магнитной индукции достаточно легко определить магнитную индукцию таких сложных магнитных полей как у соленоида и тороида.
Соленоидом называется цилиндрическая катушка, которая состоит из множества витков проводника, намотанных виток к витку на цилиндрический каркас. Магнитное поле соленоида фактически состоит из множества магнитных полей кругового тока с общей осью, перпендикулярной к плоскости каждого кругового тока.
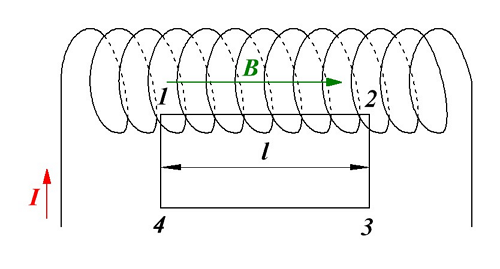
Воспользуемся циркуляцией вектора магнитной индукции и представим циркуляцию по прямоугольному контуру 1-2-3-4. Тогда циркуляция вектора магнитной индукции для данного контура будет иметь вид
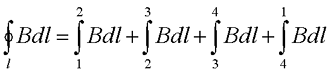
Так как на участках 2-3 и 4-1 вектор магнитной индукции перпендикулярен к контуру, то циркуляция равна нулю. На участке 3-4, который значительно удалён от соленоида, то его так же можно не учитывать. Тогда с учётом закона полного тока магнитная индукция в соленоиде достаточно большой длины будет иметь вид
где n – число витков проводника соленоида, которое приходится на единицу длины,
I – ток, протекающий по соленоиду.
Тороид образуется путём намотки проводника на кольцевой каркас. Данная конструкция эквивалентна системе из множества одинаковых круговых токов, центры которых расположены на окружности.
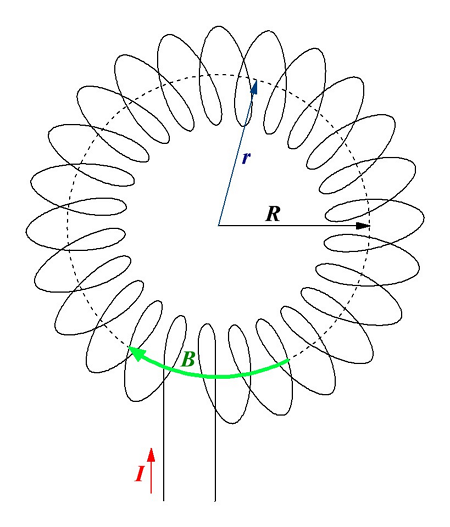
В качестве примера рассмотрим тороид радиуса R, на который намотано N витков провода. Вокруг каждого витка провода возьмём контур радиуса r, центр данного контура совпадает в центром тороида. Так как вектор магнитной индукции B направлен по касательной к контуру в каждой точке контура, то циркуляция вектора магнитной индукции будет иметь вид
где r – радиус контура магнитной индукции.
Контур проходя внутри тороида охватывает N витков провода с током I, тогда закон полного тока для тороида будет иметь вид
где n – число витков проводника, которое приходится на единицу длины,
r – радиус контура магнитной индукции,
R – радиус тороида.
Таким образом, используя закон полного тока и циркуляцию вектора магнитной индукции можно рассчитать сколь угодно сложное магнитное поле. Однако закон полного тока дает правильные результаты только лишь в вакууме. В случае расчёта магнитной индукции в веществе необходимо учитывать так называемые молекулярные токи. Об этом пойдёт речь в следующей статье.
Что такое магнитное поле?
В одной из предыдущих статей, рассказывая об электрическом поле, я упомянул, что оно является частью общего электромагнитного поля. Не трудно догадаться, что второй частью является магнитное поле, дополняющее картину взаимодействия электрических зарядов.
Использование магнитов началось давно, так, к примеру, магнитный компас используется уже более 4000 лет, а исследованиями магнитных полей занялись в XIII веке. Однако магнетизм, как наука стал распространяться только с XVII века с работ Уильям Гильберт Колчестера. С момента открытия электричества и исследования электрических явлений, стало ясно, что электрические и магнитные явления взаимосвязаны. Данную связь исследовали Андре-Мари Ампер и Джеймс Клерк Максвелл.
В результате этих исследований было установлено, что существуют тела, которые обладают следующими свойствами:
— данные тела притягивают металлические предметы;
— если проводник с током поместить возле данного тела, то на данный проводник будет действовать некоторая сила, которая заставляет перемещаться данный проводник с током;
— если проводник перемещать возле таких тел, то на концах проводника появляется ЭДС (электродвижущая сила), то есть напряжение.
Тела вокруг, которых наблюдались данные явления, назвали магнитами, а пространство вокруг магнитов – магнитными полями. Магнитное поле на поверхности магнита имеет максимальное значение в некоторых точках, которые назвали полюсами магнита. Каждый магнит имеет два полюса: северный, обозначаемый буквой N и южный, имеющий обозначение – S. Магнитное поле состоит из силовых линий, направление, которых приняли считать от северного полюса к южному полюсу.
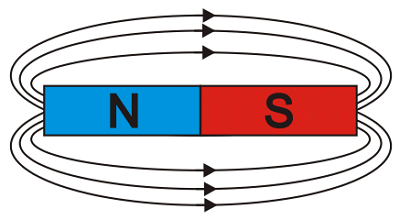
Изначально для получения магнитного поля использовали природными магнитами, но после того как обнаружили явление электромагнетизма, то есть свойство проводника с электрическим током, создавать магнитное поле, то начали использовать электромагниты.
Примечания
-
Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид:
- F→=qE→+qv→×B→.{\displaystyle {\vec {F}}=q{\vec {E}}+q.}
При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведённую в основном тексте.
- Это определение с современной точки зрения менее фундаментально, чем приведённое выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
- То есть в наиболее фундаментальном и простом для ознакомления виде.
- То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближённо — если изменения настолько медленны, что ими можно пренебречь.
- Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в статье далее).
Источники магнитного поля
Приведенный выше эксперимент наглядно демонстрирует, как любой человек может определить направление силовых линий магнитного поля Земли. Стрелка прибора покажет направления на южный и северный полюс. Продольная ось этого индикатора будет совпадать с вектором (В).
Электромагнитное поле проводника
Если аналогичный опыт выполнить около проводника с током, по движению стрелки можно определить круговое расположение силовых линий. Они образуют замкнутые кольца, перпендикулярные осевой линии кабеля.
Электромагнитная индукция
Достаточно сильное поле образует индукционная катушка. Практический пример – соленоид реле или запорного устройства. При включении такой узел втягивает внутрь металлический сердечник.
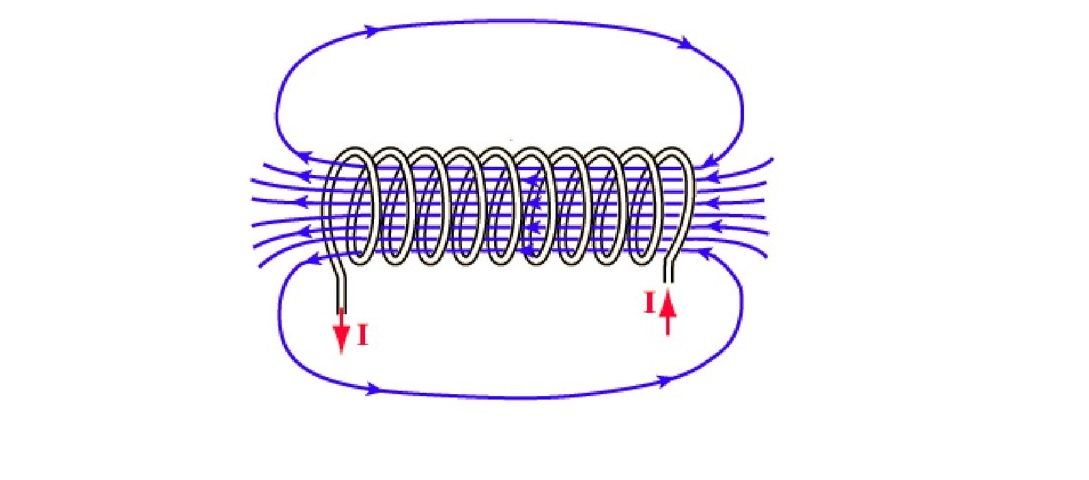 Схематический рисунок поясняет направление втягивающей силы, которая образуется в центральной оси соленоида
Схематический рисунок поясняет направление втягивающей силы, которая образуется в центральной оси соленоида