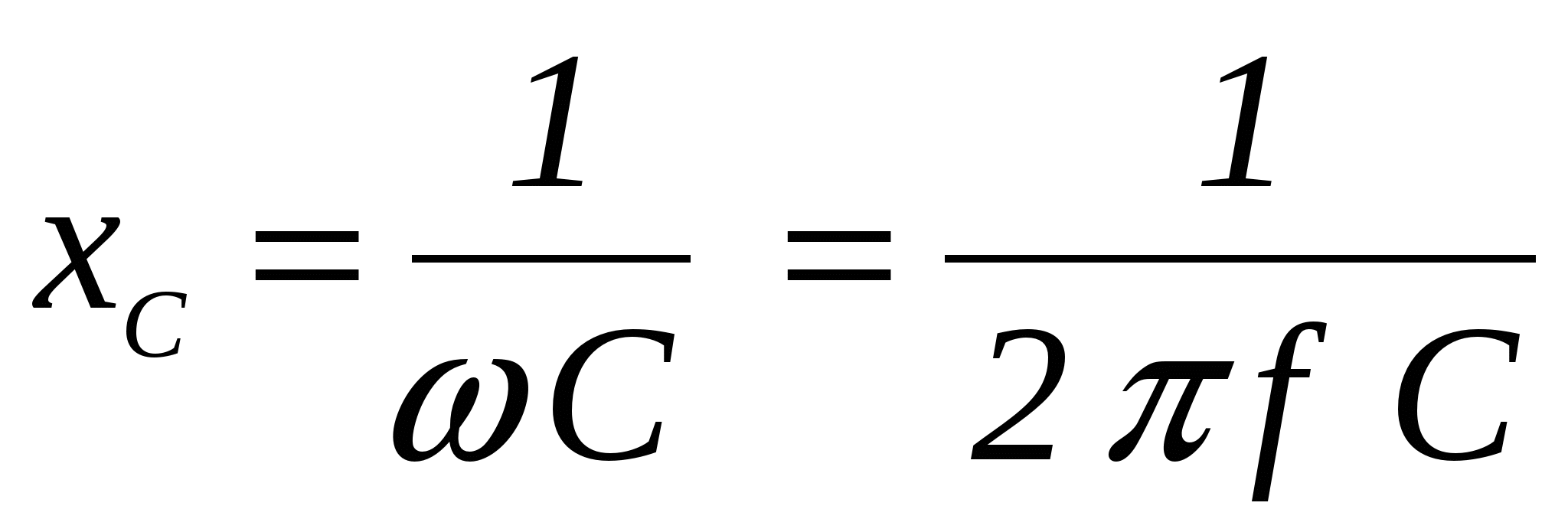Реактивное сопротивление

Что такое активное сопротивление

Активное нагрузочное сопротивление – это та его форма, которая наблюдается при безвозвратной трансформации электрической энергии в другие ее виды, например, тепловую (как в электроплите), световую или механического движения. На элементе, имеющем активное сопротивление, падает цепное напряжение, притом, чем больше падение, тем больше  значение резистивности. Кроме того, когда по такому компоненту идет ток, происходят безвозвратные потери мощности. В качестве иллюстрации можно упомянуть выделение тепла на резисторе. Таким противодействием обладают также проводники и конфигурации из них, в том числе кабели, которыми компоненты цепи соединяют друг с другом, и обмотки электрических моторов.

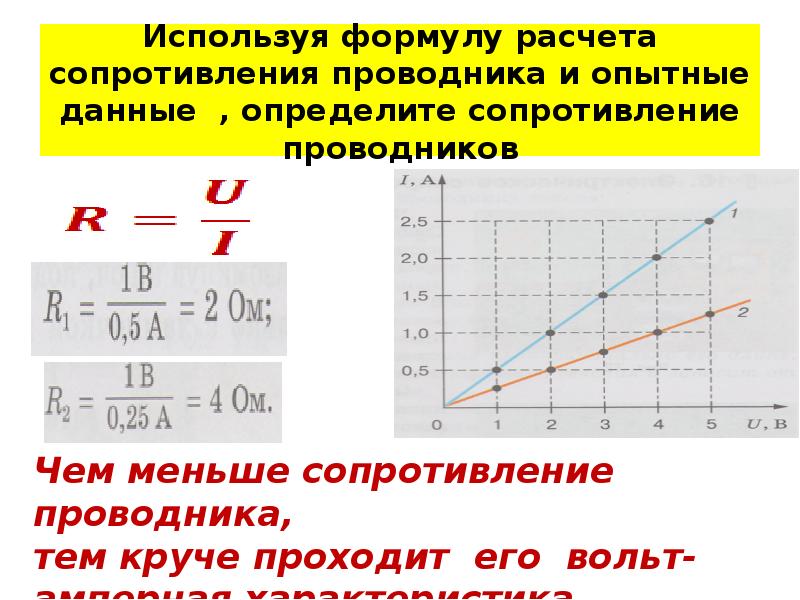
Определение значения осуществляется посредством формулы:

R=U/I.

Напряжение на детали делится на проходящий через нее электроток. На результат влияют различные характеристики провода: материал, конфигурация, геометрические параметры, температура.

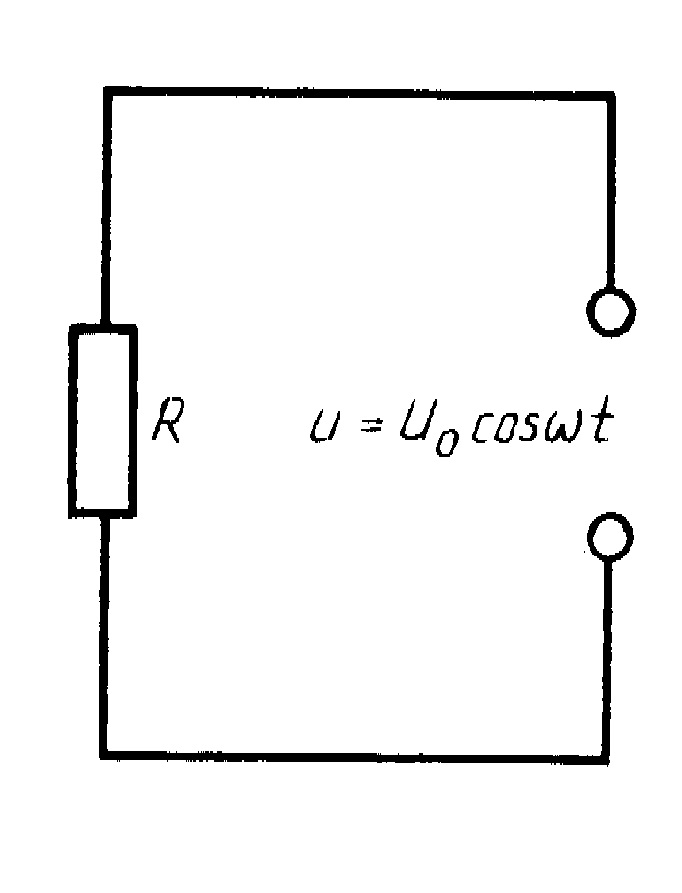Цепь с резисторным компонентом

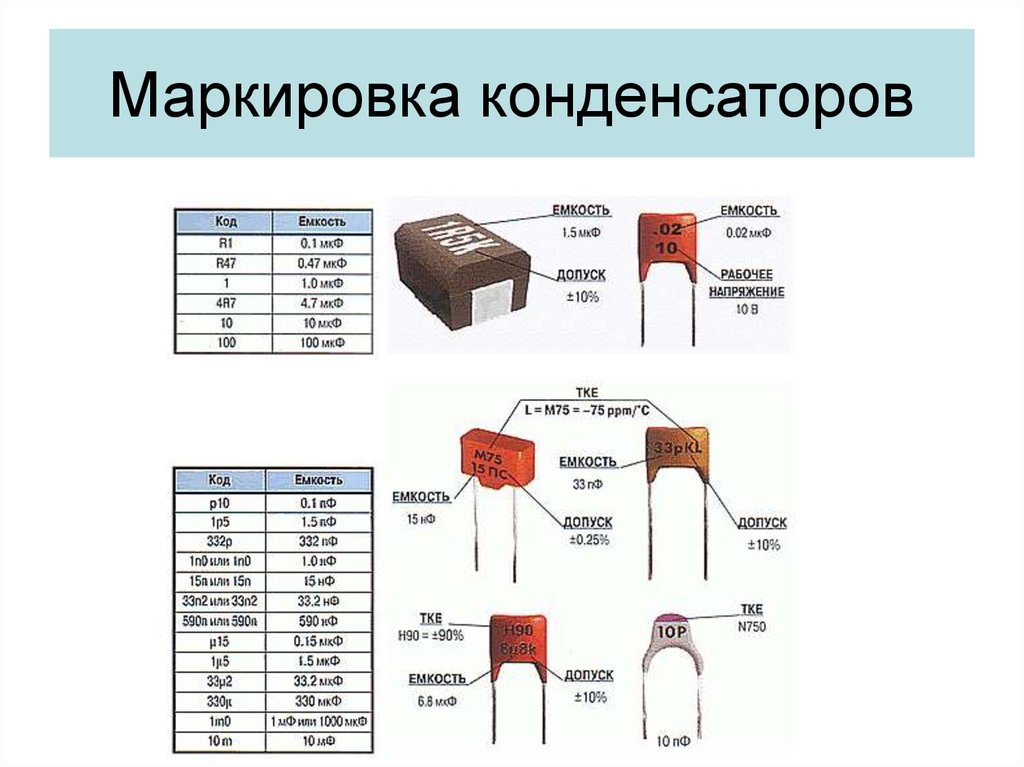
Характеристики реактивного конденсатора

Параметры, характеризующие элементы, наносятся на их внешних корпусах, там же прописываются сведения о типе, наименовании изготовителя и дате выпуска продукции.

Перечень основных критериев:

Номинальная ёмкость – это значение, определенное ГОСТом, задаваемое в диапазоне 0 – 9999 Пф, наносимое на схемы, но без обозначений. Если числа указываются на самом конденсаторе в пределах от 10000 до 9999 в мкФ, то значения надписываются в мкФ (uF).

Единицы

• Далее – наносятся условные отклонения от номинала.
• Еще один важный параметр – показатель номинального напряжения (В). Специалистами рекомендовано использовать в работе элемент с дополнительными ресурсами. Не допускается применять прибор с меньшими показателями, для предотвращения пробоя изоляции из диэлектрического материала, что провоцирует поломку детали.
• Иные характерные параметры на корпусах – рабочая температура, показатель предельной силы тока.
• Количество фаз, от которых осуществляется работа – одна или три.
• По виду установки: внутренняя и наружная.

Важно! Перечисленные критерии можно увидеть на корпусной детали, а расчет реактивного сопротивления выполнить самостоятельно. Дополнительные характеристики устройства для накопления зарядов:

Дополнительные характеристики устройства для накопления зарядов:

• Удельная ёмкость – это отношение непосредственных габаритов к массе диэлектрического элемента.
• Рабочее напряжение – это номинал, который выдерживает деталь при подаче напряжения на изоляцию.
• Стабильность температуры. В этом диапазоне изменений не отмечается.
• Сопротивление изоляционного слоя. Этот параметр определяется исходя из тока утечки и саморазряда.

Поле

• Эквивалентное сопротивление – обуславливается потерями на выводах и в диэлектрическом слое.
• Процесс адсорбции. Это разность потенциалов, образовавшаяся на обкатках после обнуления заряда.
• Сопротивление емкости. Возникает при снижении проводимости подачи переменного тока.
• Полярность. При приложении потенциала с соответствующим значением конденсатор функционирует корректно.
• Эквивалентная индуктивность. Это параметр, образующийся на контактах, для возникновения колебательного контура.

Характеристики

Как рассчитать потерю напряжения?

Калькулятор в режиме онлайн позволяет правильно вычислить необходимые параметры, которые в дальнейшем сократят появление различного рода неприятностей. Для самостоятельного вычисления потери электрического напряжения используют следующую формулу:

U =(P*ro+Q*xo)*L/U ном:

• Р – это активная мощность. Её измеряют в Вт;
• Q – реактивная мощность. Единица измерения вар;
• ro – выступает в качестве активного сопротивления (Ом);
• хо – реактивное сопротивление (м);
• U ном – это номинальное напряжение (В). Оно указывается в техническом паспорте устройства.

Согласно правилам устройства электроустановок (ПУЭ) допустимой нормой возможных отклонений напряжения принято считать:

• в силовых цепях оно может составлять не выше +/- 6%;
• в жилом пространстве и за его пределами до +/- 5%;
• на производственных предприятиях от +/- 5% до -2%.

Потери электрического напряжения от трансформаторной установки до жилого помещения не должны превышать +/- 10%.

В процессе проектирования, рекомендуется сделать равномерную нагрузку на трехфазной линии. Допустимая норма составляет 0,5 кВ. В ходе монтажных работ электродвигатели необходимо подключить к линейным проводникам. Линия освещения будет заключена между фазой и нейтралью. В результате этого, нагрузка правильно распределяется между проводниками.

Когда рассчитывают потерю напряжения в кабеле, за основу берут данные значения тока или мощности. На протяженной электрической линии учитывают индуктивное сопротивление.

Как снизить потери ?

Одним из способов снижения потери напряжения в проводнике, является увеличение его сечения. Помимо этого, рекомендуется сократить его протяженность и удаленность от точки назначения. В некоторых случаях эти способы не всегда можно применить по техническим причинам.В большинстве случаем, сокращение сопротивления позволяет нормализовать работу линии.

Главным недостатком большой площади сечения кабеля, являются существенные материальные затраты в процессе использования. Именно поэтому правильный расчёт и подбор нужного диаметра, позволяют избавиться от этой неприятности. Калькулятор в режиме онлайн применяют для проектов с высоковольтными линиями. Здесь программа помогает правильно рассчитать точные параметры для электрической цепи.

Основные причины появления потери напряжения

Большие потери электрического напряжения возникают в из – за чрезмерного рассеивания энергии. В результате этого, поверхность кабеля сильно нагревается, тем самым провоцируя деформирование изоляционного слоя. Такое явление распространено на высоковольтных линиях, где отмечают большие нагрузки.

Чаще всего существенные потери наблюдают на протяженных электролиниях. Помимо этого, здесь отмечают большие финансовые расходы на электричество в процессе эксплуатации.

Таблица потерь напряжения по длине кабеля

Определение потерь напряжения по длине кабеля

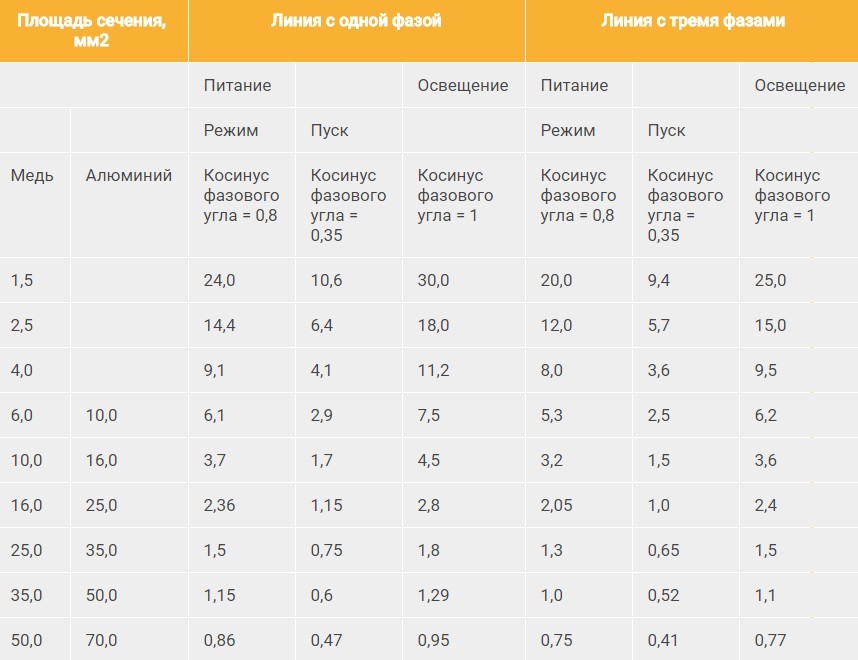
Воспользуйтесь другими онлайн калькуляторами:

• Расчет веса электрического кабеля
• Онлайн расчет силы тока в цепи
• Перевод Ватт в Амперы
• Расчет катушки индуктивности
• Онлайн расчет сечения кабеля

Практическое использование реактивного сопротивления

С помощью конденсаторных установок осуществляется компенсация реактивной мощности. Через электрические сети высоковольтная электроэнергия передается на большие расстояния. В большинстве случаев она потребляется электродвигателями с резистивными элементами и значительным индуктивным сопротивлением.

Полная мощность, поступающая к потребителям, включает в себя активную составляющую Р, с помощью которой совершается полезная работа, и реактивную составляющую Q, приводящую к нагреву обмоток электродвигателей и трансформаторов. Качество электроэнергии существенно снижается под действием реактивной составляющей, возникающей на индуктивных сопротивлениях. Для того чтобы ликвидировать ее негативное воздействие, была разработана специальная схема компенсации. С этой целью подключались конденсаторные батареи, емкостное сопротивление которых способствовало понижению косинуса угла ф.

Установка таких конденсаторных батарей практиковалась в основном на подстанциях, осуществляющих непосредственную поставку электроэнергии проблемным потребителям. Данное мероприятие позволяло эффективно регулировать качество поставляемой энергии.

Снижение уровня реактивной компоненты способствует существенному уменьшению нагрузки на установленное оборудование, хотя активная мощность остается на одном и том же уровне. Используя реактивное сопротивление конденсатора, удалось добиться экономии электроэнергии на предприятиях промышленного производства и объектах жилищно-коммунального хозяйства, повысить надежность работы энергетических систем.

Индуктивность в электрических цепях

В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.

В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:

Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:

где ω является угловой частотой резонансной частоты F:

Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.

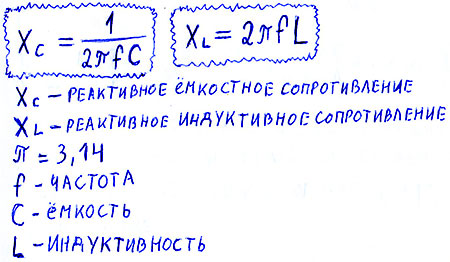
 Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.

Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:

Особые режимы работы цепи

Нажмите на соответствующую ссылку, чтобы посмотреть как работает калькулятор в особых режимах:

Примечания

• Нулевая частота в объяснениях поведения этой цепи означает постоянный ток. Если f = 0, предполагается, что цепь подключена к идеальному источнику напряжения.
• При нулевой частоте реактивное сопротивление конденсатора считается нулевым, если его емкость бесконечно большая. Если же емкость конденсатора конечная или нулевая, его реактивное сопротивление бесконечно большое и для источника постоянного напряжения он представляет собой обрыв цепи, иными словами отсутствующий конденсатор.
• При нулевой частоте реактивное сопротивление идеальной катушки индуктивности считается бесконечно большим, если ее индуктивность бесконечно большая. Если же индуктивность катушки конечная или нулевая, ее реактивное сопротивление при нулевой частоте равно нулю и для источника постоянного напряжения она представляет собой короткое замыкание.

Катушки индуктивности в высокочастотном модуле телевизионного приемника

Области проявления

Реактанс электросопротивления проявляется в емкости и индукции. Первое обуславливается наличием емкости проводниках и обмотках или включением в электрическую цепь переменного тока различных конденсаторов. Чем выше емкость потребителя и угловой частоты сигнала электротока, тем меньше емкостная характеристика.

Сопротивляемость, которую оказывает проводник переменному току и электродвижущей силе самоиндукции, называется индуктивным. Оно зависит от индуктивности потребителя. Чем выше его индуктивность и выше частота переменного электротока, тем выше индуктивное электросопротивление. Выражается оно формулой: xl = ωL, где xl — это электросопротивление индукции, L — индуктивность, а ω — угловая частота тока.

Емкостный реактанс электросопротивление проявляется, например, в конденсаторе, который накапливает электроэнергию в виде электромагнитного поля между своими обкладками. Индуктивное электросопротивление можно наблюдать в дросселе, который накапливает энергию в виде магнитного поля внутри своей обмотки.

Активностным же электросопротивлением может обладать любой резистор, линии электропередач, обмотки трансформатора или электрического двигателя.

Индукция ЭДС может наблюдаться в дросселе

Таким образом, активный резист и реактанс во многом отличаются друг от друга не только разницей по названию, но и по физическим свойствам. Первый вид превращает электроэнергию в другой вид и отдает ее в окружающую среду. Второй же — возвращает ее обратно в электросеть.

Расчет эквивалентного сопротивления элементов цепи

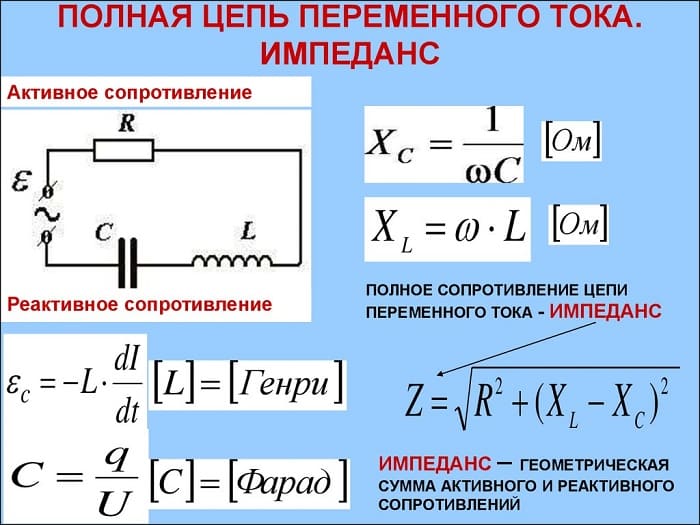
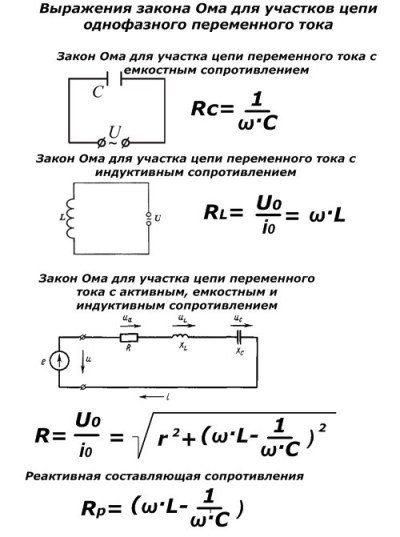
Определение общего цепного сопротивления будет зависеть от того, какого типа конфигурацию составляют компоненты цепи. Для параллельного и последовательного подключений правила расчета будут неодинаковыми. Опираться при вычислениях нужно на закон Ома.

Согласно ему, у всех последовательно соединенных деталей, подключенных в цепь переменного тока, будет одно и то же значение электротока:

I=U/Z, где Z – общий импеданс цепи.

Напряжения будут различаться и окажутся привязанными к сопротивлениям деталей: на концах резистора его значение будет равно UR = IR (здесь R – активная резистивность элемента), для дросселя – UL = IXL, для емкостного элемента – UC = IXC (XL и XC – реактивные показатели соответствующих устройств). Так как векторы напряженности катушки и конденсатора имеют противоположные направления, суммарный показатель на реактивных деталях будет равен: UX = UL – UC . Противодействие будет равно: X = XL – XC.

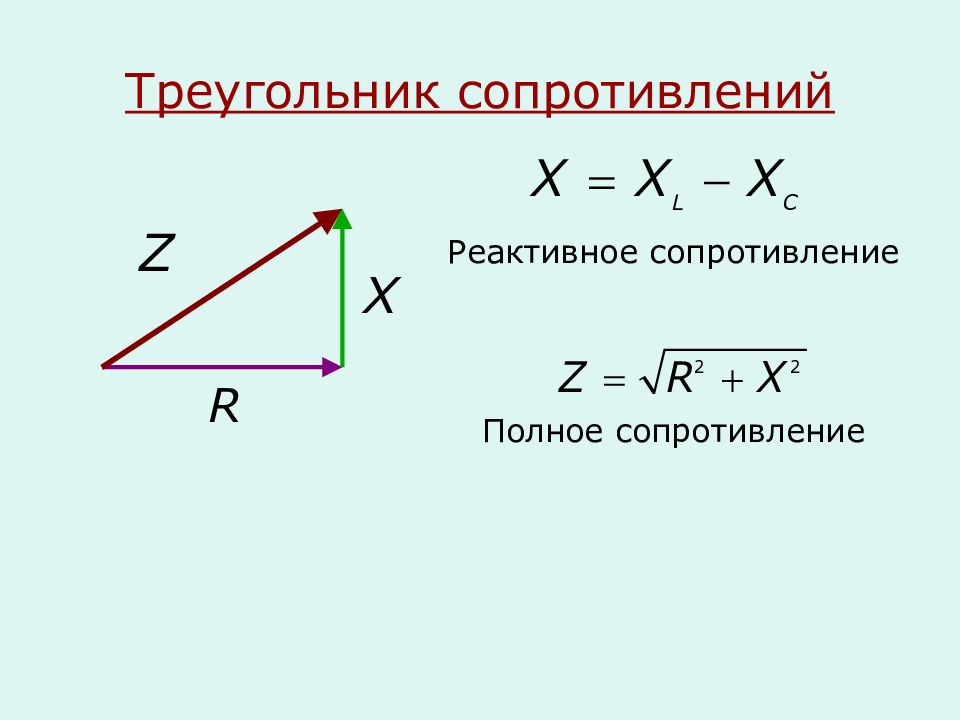
Напряжения (общее, реактивное и активное) могут быть представлены в виде прямоугольного треугольника. Из него получается, что U² = UR² + UX². Поскольку противодействия входящих в цепь компонентов пропорциональны напряжениям, имеем Z2=R2+X2=R2+(XL – XC)2.

Для параллельного соединения принято выводить значения импеданса из проводимостей элементов, которые обратны их сопротивлениям. Отсюда 1/z2 = 1/R2 + 1/X2. Таким образом, выходит следующая формула:

Z2=1/(1/R2+(1/ XL – 1/ XC)2).

Общее сопротивление определяется компонентным составом цепи и характером соединения ее элементов. При расчетах показателей используется закон Ома.

Список литературы

1. Brehm, J. W. (1966). A theory of psychological reactance. Academic Press.
2. Brehm, S. S., & Brehm, J. W. (1981). Psychological Reactance: A Theory of Freedom and Control. Academic Press.
3. Miller, C. H., Lane, L. T., Deatrick, L. M., Young, A. M., & Potts, K. A. (2007). Psychological reactance and promotional health messages: The effects of controlling language, lexical concreteness, and the restoration of freedom. Human Communication Research, 33, 219—240.
4. Аронсон Э. Общественное животное. Введение в социальную психологию. изд. 7.; пер. с англ. — М.: Аспект Пресс, 1998. — 517 с
5. Майерс Д. Социальная психология. изд 7.; пер с англ. — СПб.: Питер, 1997. — 688 с.

Особенности активного сопротивления

В общем виде данный параметр выглядит, как противодействие определенного участка цепи проходящему по нему току. Полученная в результате такого процесса величина участвует в преобразовании энергии и ее переходе в какое-то другое состояние.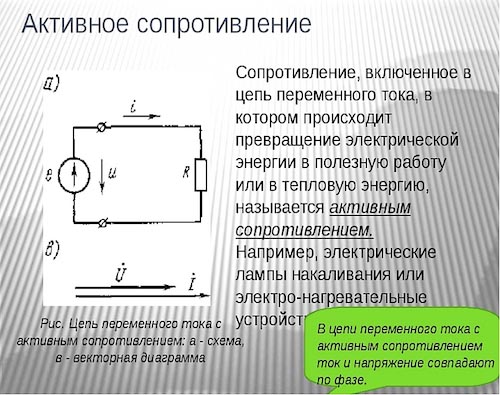

Величина активного сопротивления обусловлена эффектом поверхностного типа. Наблюдается процесс своеобразного перемещения тока от центра к поверхности проводника. Сечение кабеля используется не полностью, а возникающее противодействие будет значительно превышать аналогичный омический показатель.

Обратим внимание на такой момент:

Поверхностный эффект имеет незначительную величину в линиях из металлов, относящихся к категории цветных. Активное сопротивление приравнивают к омическому и считают его при условной температуре в +20°С, без учета фактических показателей окружающей среды. В справочниках имеются данные определения для использования в основном выражении R=r0l, с учетом того, что r0 – это номинальное значение искомой величины для 1 км провода, а l – его фактическая протяженность.
А вот в стальных изделиях данный показатель намного выше

Обязательно потребуется брать во внимание, зависящее от сечения явление перемагничивания и влияние таких компонентов, как вихревые токи. На практике обычно при больших нагрузках пользуются справочными данными

При этом, само явление ослабевает в проводниках многопроволочного типа.

Полезные примеры из жизни

Как продлить ресурс лампы накаливания

В пожарном депо Ливермоля (Калифорния) зарегистрирован рекорд рабочего режима осветительной лампы: 117 лет. Она практически непрерывно выполняет свою задачу с 1901 года по настоящее время.

Такой ресурс обеспечен за счет:

• правильного выбора сопротивления, ограничивающего ток через нить накала и создания экономного режима освещения;
• беспрерывной работы, исключающей переходные процессы при включениях/выключениях, сопровождаемые бросками токов;
• надежной конструкции.

Как регулировать токи от 100 ампер в силовой цепи

Этот случай я привожу не для повторения, а с целью расширения кругозора и лучшего уяснения процессов, происходящих в электричестве.

Ни один обычный резистор не способен длительно выдерживать токи такой величины. Он просто сгорит. Однако при наладке промышленных генераторов требуется иметь устройство, справляющееся с подобными мощностями.

Это водяной реостат, состоящий из металлического корпуса — ведра прямоугольной формы, служащего одним из контактов для подключения провода от нагрузки.

Второй контакт составляет металлический нож, подключаемый через изоляторы.

Внутрь ведра наливают воду и засыпают соль: создают электролит, хорошо проводящий большие токи.

Перемещение ножа в электролите меняет сопротивление среды и обеспечивает регулировку высоких токов. Проводимость можно изменять концентрацией соли в растворе.

Напоминаю: подобное устройство нельзя использовать в бытовых цепях: оно не отвечает требованиям безопасности.

Таким образом, под каждый конкретный случай расчета используется своя формула электрического сопротивления, которой следует внимательно пользоваться. Исключить ошибки в расчетах помогает специализированный онлайн калькулятор.

По этой теме рекомендую посмотреть видеоролик Владимира Романова.

Если хотите задать вопрос или дополнить информацию, то воспользуйтесь разделом комментариев.

Примечания[править | править код]

1. Shamieh C. и McComb G., Electronics for Dummies, John Wiley & Sons, 2011.
2. Мид Р., Основы электроники, Cengage Learning, 2002.
3. Young, Hugh D.; Roger A. Freedman; A. Lewis Ford (2004) . Сирс и Земанский университет физики (11-е изд.). Сан-Франциско : Эддисон Уэсли . ISBN Young, Hugh D.; Roger A. Freedman; A. Lewis Ford (2004) . Young, Hugh D.; Roger A. Freedman; A. Lewis Ford (2004) .

1. ↑ Irwin, D. (2002). Basic Engineering Circuit Analysis, page 274. New York: John Wiley & Sons, Inc.
2. Hayt, W.H., Kimmerly J.E. (2007). Engineering Circuit Analysis, 7th ed., McGraw-Hill, p. 388
3. ↑ Glisson, T.H. (2011). Introduction to Circuit Analysis and Design, Springer, p. 408
4. Horowitz P., Hill W. (2015). The Art of Electronics, 3rd ed., p. 42
5. ↑ Hughes E., Hiley J., Brown K., Smith I.McK., (2012). Hughes Electrical and Electronic Technology, 11th edition, Pearson, pp. 237—241
6. Robbins, A.H., Miller W. (2012). Circuit Analysis: Theory and Practice, 5th ed., Cengage Learning, pp. 554—558

Почему проводник “сопротивляется”?

Напряжение U, поданное на концы проводника, создает внутри него электрическое поле, которое приводит в движение свободные электроны вещества. Электроны, получив дополнительную кинетическую энергию, начинают двигаться упорядоченно в одном направлении, создавая тем самым электрический ток цепи.

В процессе движения электроны сталкиваются с нейтральными и заряженными атомами, из которых стоит проводник, теряют энергию. Масса атома превосходит массу электрона в тысячи раз, поэтому их столкновение приводит к изменению направления движения электронов и потере скорости (“торможению”).

Рис. 1. Электрический ток в проводнике ограничивается столкновением электронов с атомами.

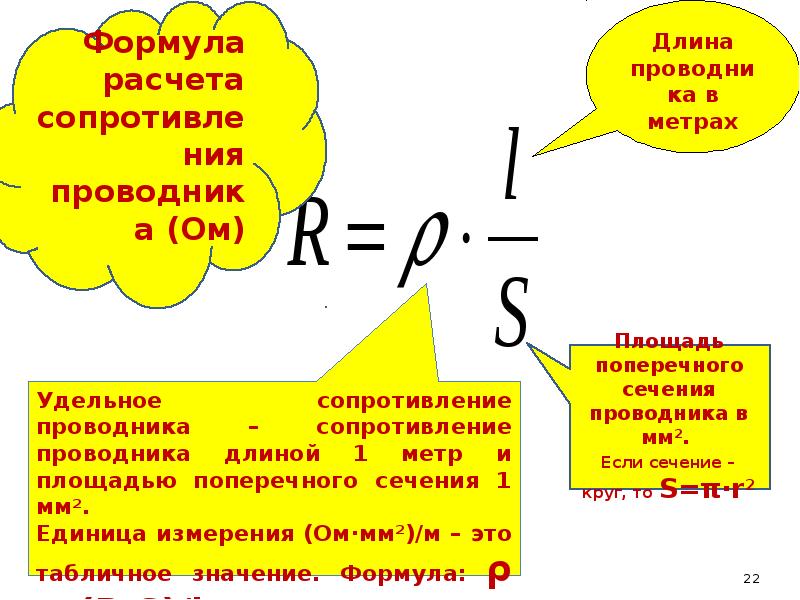
Расчет с помощью удельного сопротивления

Расчет сопротивления проводника можно произвести без измерения величин напряжения и тока. Но для этого необходимо знать дополнительную информацию о проводнике.

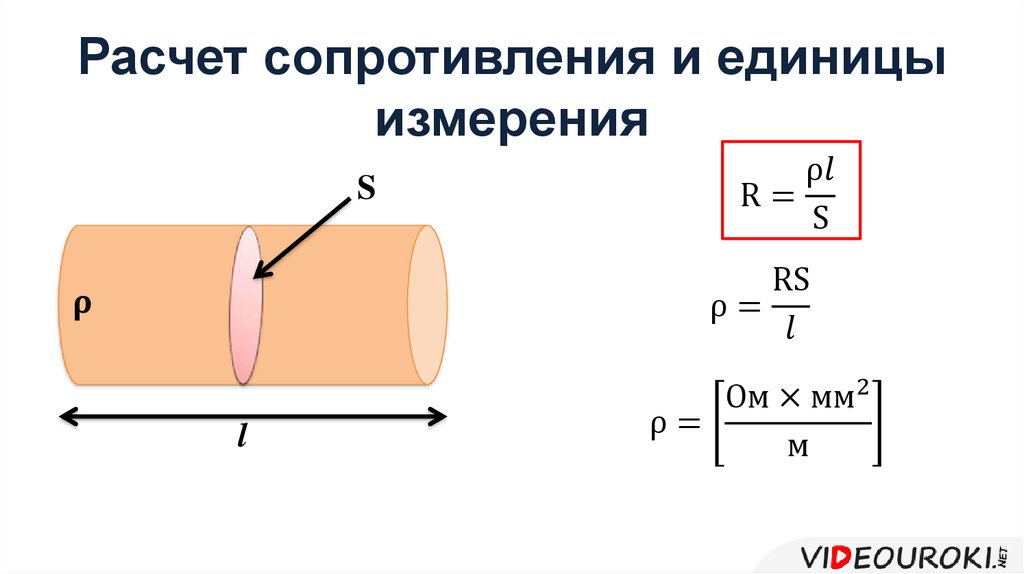
Рис. 3. Проводник с поперечным сечением S и длиной L, через который течет ток I.

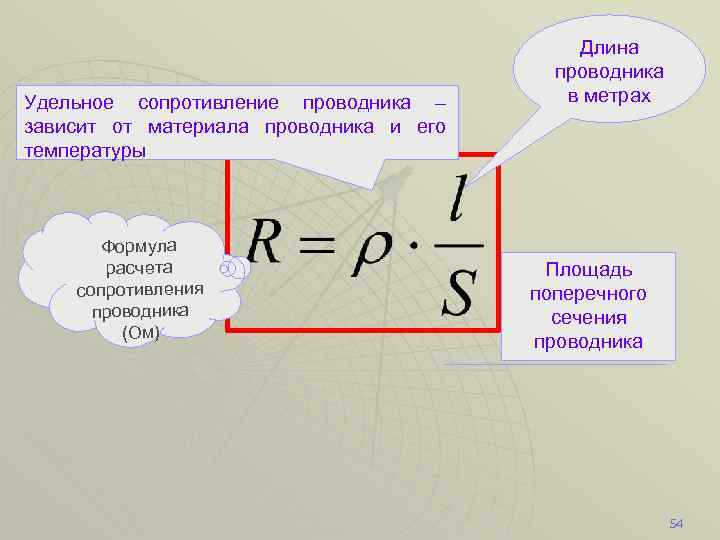
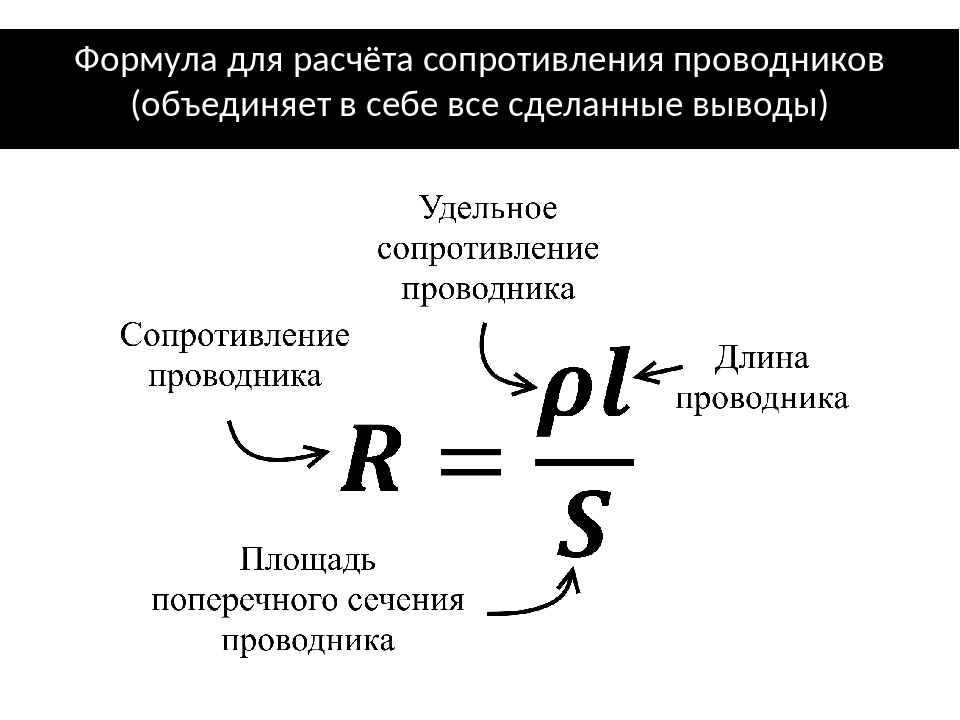
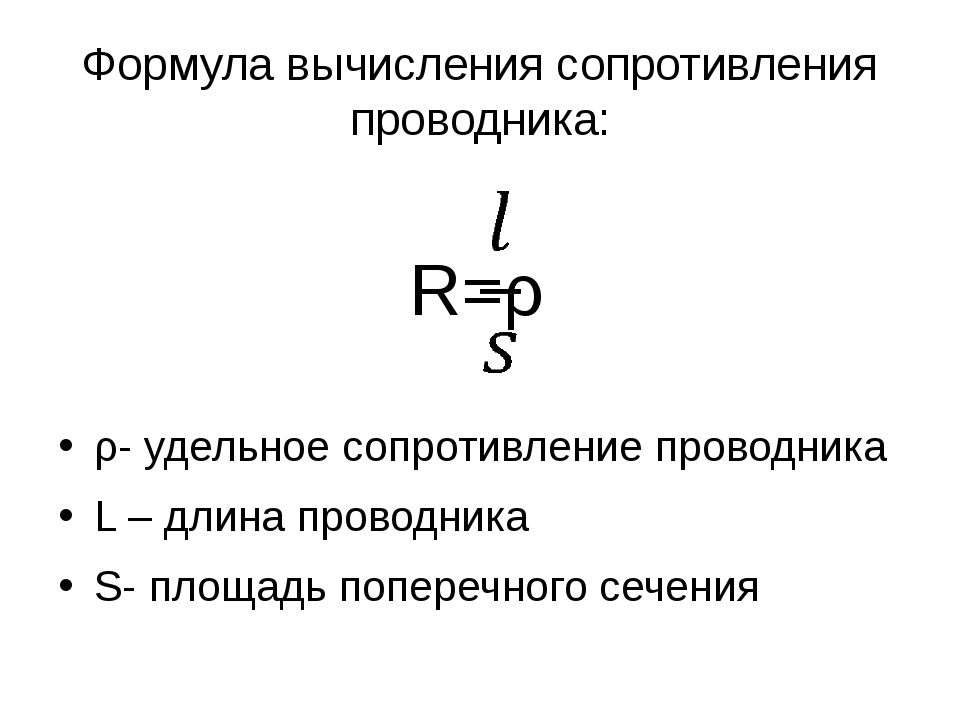
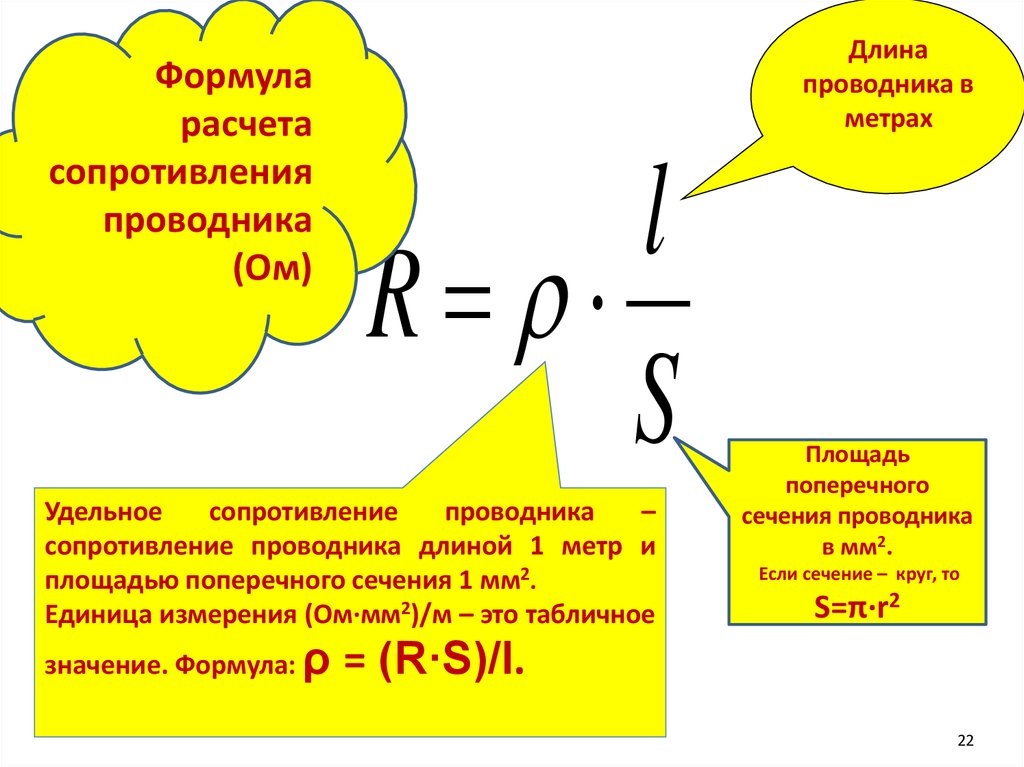
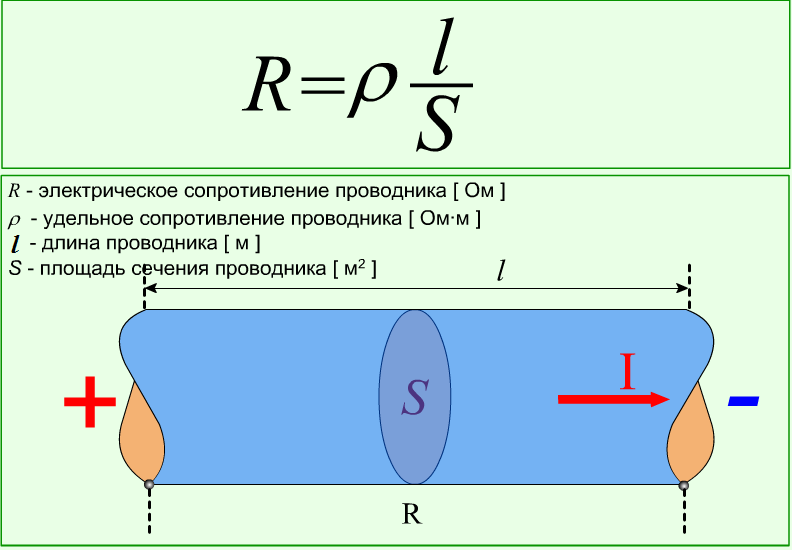
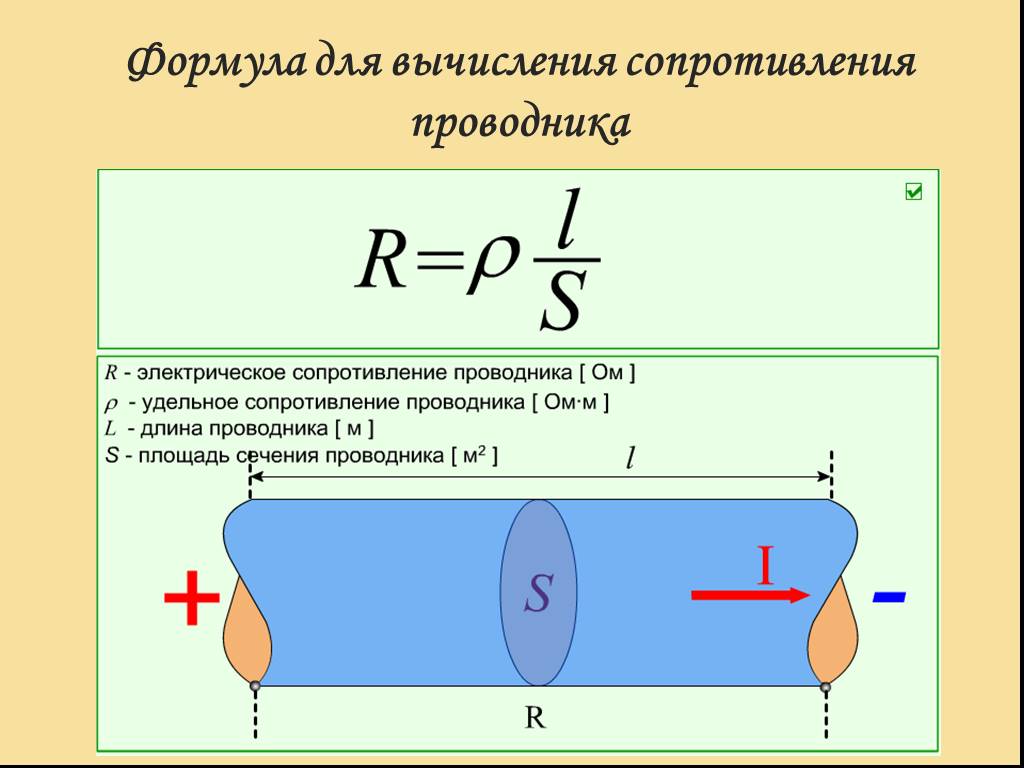
Георг Ом и другие исследователи опытным путем определили, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника S. Эту закономерность можно описать формулой расчета сопротивления проводника:

$ R = ρ *{ L\over S} $ (2)

Коэффициент ρ был назван удельным сопротивлением. Эта физическая величина отражает особенности конкретного вещества, которые зависят от плотности вещества, кристаллической структуры, строения атомов и других внутренних параметров. Расчет удельного сопротивления проводника производить каждый раз необязательно, так как для большинства веществ удельные сопротивления измерены и сведены в справочные таблицы, которые можно найти в бумажных справочниках или в их интернет-версиях.

Но если такая необходимость возникнет, то из формулы (2) можно получить следующую формулу (3), и по ней рассчитать ρ:

$ ρ = R*{ S\over L } $ (3)

Серебро имеет одно из самых низких значений ρ, равное $ 0,016 {Ом*мм^2\over м} $. Этим объясняется использование такого довольно дорогого металла для пайки особенно важных радиодеталей (микросхем, микропроцессоров, электронных плат), которые должны как можно меньше нагреваться в процессе работы.

Что мы узнали?

Итак, мы узнали, что расчет сопротивления проводника можно произвести двумя способами. Первый расчет проводится с помощью формулы закона Ома после измерения величин напряжения и тока. Для второго расчета необходима информация о геометрических размерах проводника и его удельном сопротивлении.

Особенность активного и реактивного сопротивления

Сеть с переменным током обладает необратимой трансформацией и передачей энергии элементам электрической цепи. Осуществляя обменный процесс электроэнергии с компонентами цепи и источником питания, сопротивление будет реактивным.

Если в качестве примера рассматривать микроволновую печь, электрическая энергия в ней необратимо конвертируется в тепловую, в результате чего микроволновая печь получает активное противодействие, равно как элементы, трансформирующие электрическую энергию в световую, механическую и т. д.

Активное сопротивление находится в прямой зависимости от количества полных циклов изменения электродвижущей силы (ЭДС), произошедших за одну секунду. Чем больше это количество, тем выше активное сопротивление.

https://youtube.com/watch?v=TMKBh18LKcw

Однако немало потребителей имеют индуктивные и емкостные свойства в момент прохождения сквозь них переменного тока. К ним можно отнести:

• конденсаторы;
• дроссели;
• электромагниты;
• трансформаторы.

Следует учитывать как активное, так и реактивное сопротивление, которое обусловлено присутствием в электропотребителе емкостного и индуктивного признака. Прерывая и замыкая цепь постоянного тока, проходящего по любой из обмоток, параллельно с преобразованием тока произойдет и изменение магнитного потока внутри самой обмотки, в итоге в ней появляется электродвижущая сила самоиндукции.

Аналогичная ситуация будет проявляться и в обмотке, подключенной к цепи с переменным током, с тем лишь отличием, что в этом случае ток беспрерывно меняется как по параметру, так и в направлении. Отсюда следует, что беспрерывно будет меняться параметр магнитного потока, проникающего в обмотку, в которой индуктируется электродвижущая сила самоиндукции.

Получается, что ЭДС, появляющаяся внутри проводника (обмотки), задействованного в цепи переменного тока, постоянно будет противодействовать току, препятствуя его изменению. Другими словами, ЭДС можно расценивать как вспомогательное сопротивление, которое совместно с активным сопротивлением катушки создает синергический эффект противодействия идущему через катушку переменному току.

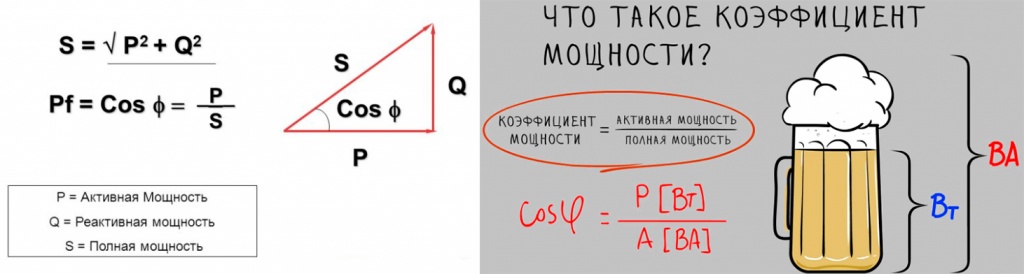
Сравнение влияния реактивного сопротивления на активную мощность сети

Из рисунков 1 и 2 видно, что сдвиг фаз на рисунках не одинаков. Вывод — чем больше в полном сопротивлении Z будет влияние X_Lили  X_C  тем больше будет разница фаз U и I.

Угол сдвига между током и напряжением называется φ .

Реактивная мощность однофазная:

Трехфазная:

U_ф, I_ф — фазные ток и напряжение

Вывод: реактивная мощность – не выполняет полезного действия.

Она «перегоняется» по сети нагревая кабели и увеличивая потери. На крупных промышленных предприятиях это особо ощутимо в силу наличия электроприводов  и других крупных потребителей. Этот вопрос очень актуален для энергосбережения и модернизации производства. Поэтому на пром. предприятиях устанавливаются компенсаторы реактивной мощности. Они могут быть разного типа и кроме компенсации выполнять еще и роль фильтров. С помощью компенсаторов стараются сохранить баланс реактивной мощности для минимизации ее влияния на сеть и подогнать угол φ к нулю.

Для компенсации реактивной мощности необходимо максимально сбалансировать в сети количество (L, C) элементов.

От чего зависит индуктивное сопротивление

Данная величина связана напрямую с частотой приложенного напряжения (f) и значением индуктивности (L). Формула индуктивного сопротивления будет выглядеть следующим образом: XL = 2πfL. Прямая пропорциональная зависимость, в случае необходимости, позволяет путем преобразования основной формулы вычислить частоту или значение индуктивности.

Под действием переменного тока, проходящего по проводнику, вокруг этого проводника образуется переменное магнитное поле. Действие этого поля приводит к наведению в проводнике электродвижущей силы обратного направления, известной еще как ЭДС самоиндукции. Противодействие или сопротивление ЭДС переменному току получило название реактивного индуктивного сопротивления.

Существует такое понятие, как погонное индуктивное сопротивление, которое вычисляется по формуле: X0 = ω x (4,61g x (Dср/Rпр) + 0,5μ) x 10-4 = X0’ + X0’’, в которой ω является угловой частотой, μ – магнитной проницаемостью, Dср – среднегеометрическим расстоянием между фазами ЛЭП, а Rпр – радиусом провода.

Величины X0’ и X0’’ представляют собой две составные части погонного индуктивного сопротивления. Первая из них X0’ представляет собой внешнее индуктивное сопротивление, зависящее только от внешнего магнитного поля и размеров ЛЭП. Другая величина – X0’’ является внутренним сопротивлением, зависящим от внутреннего магнитного поля и магнитной проницаемости μ.

На линиях электропередачи высокого напряжения от 330 кВ и более, проходящие фазы расщепляются на несколько отдельных проводов. Например, при напряжении 330 кВ фаза разделяется на два провода, что позволяет снизить индуктивное сопротивление примерно на 19%. Три провода используются при напряжении 500 кВ – индуктивное сопротивление удается снизить на 28%. Напряжение 750 кВ допускает разделение фаз на 4-6 проводников, что способствует снижению сопротивления примерно на 33%.

Погонное индуктивное сопротивление имеет величину в зависимости от радиуса провода и совершенно не зависит от сечения. Если радиус проводника будет увеличиваться, то значение погонного индуктивного сопротивления будет соответственно уменьшаться. Существенное влияние оказывают проводники, расположенные рядом.

Индуктивное сопротивление

Реактивное сопротивление подразделяется на два основных вида – индуктивное и емкостное.

При рассмотрении первого варианта следует отметить возникновение в индуктивной обмотке магнитного поля под действием переменного тока. В результате, в ней образуется ЭДС самоиндукции, направленной против движения тока при его росте, и по ходу движения при его уменьшении. Таким образом, при всех изменениях тока и наличии взаимосвязей, ЭДС оказывает на него противоположное действие и приводит к созданию индуктивного сопротивления катушки.

Под влиянием ЭДС самоиндукции энергия магнитного поля обмотки возвращается в электрическую цепь. То есть, между источником питания и обмоткой происходит своеобразный обмен энергией. Это дает основание полагать, что катушка индуктивности обладает реактивным сопротивлением.

В качестве типичного примера можно рассмотреть действие реактивного сопротивления в трансформаторе. Данное устройство имеет общий магнитопровод, с расположенными на нем двумя обмотками или более, имеющими общую зависимость. На одну из них поступает электроэнергия из внешнего источника, а из другой выходит уже трансформированный ток.

Под действием первичного тока, проходящего по катушке, в магнитопроводе и вокруг него происходит наведение магнитного потока. В результате пересечения витков вторичной обмотки, в ней формируется вторичный ток. При невозможности создания идеальной конструкции трансформатора, магнитный поток будет частично уходить в окружающую среду, что приведет к возникновению потерь. От них зависит величина реактивного сопротивления рассеяния, которая совместно с активной составляющей образуют комплексное сопротивление, называемое электрическим импедансом трансформатора.

Индуктивный элемент L

Индуктивный элемент ( рассмотрим на примере  катушки индуктивности) представляют собой витки изолированного между собой провода. При протекании тока катушка намагничивается. Если изменить полярность  источника, катушка начнет отдавать запасенную энергию обратно, стараясь поддержать величину тока в контуре. Поэтому при протекании через нее  переменной составляющей , энергия запасенная при прохождении положительного полупериода, не успеет рассеяться и будет препятствовать прохождению отрицательного полупериода. В результате отрицательному полупериоду придется  погасить энергию запасенную катушкой. В итоге напряжение(U),  будет опережать ток (І) на какой-то угол φ. Ниже  приведен результат моделирования работы на L-R нагрузку  L=1*10-3 Гн, R=0.5 Ом. U_ист= 250 В, частота f=50 Гц.

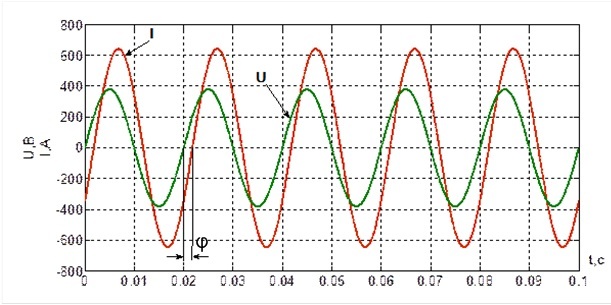Рисунок 1. Работа источника на R-L нагрузку

φ – это разница фаз  между U и  I.

Реактивное сопротивление обозначается буквой X, полное  Z, активное R.

Для  индуктивности :

Где ω – циклическая  частота 

— частота питающего напряжения,  Гц;

L – индуктивность катушки;

Вывод: чем выше индуктивность L или частота , тем больше будет сопротивление катушки переменному току.