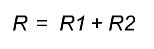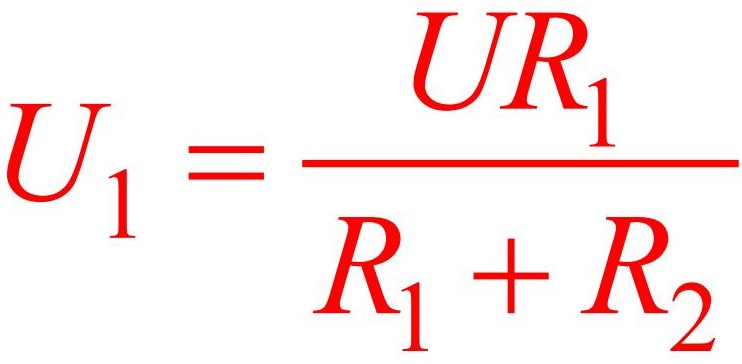- Виды резисторов
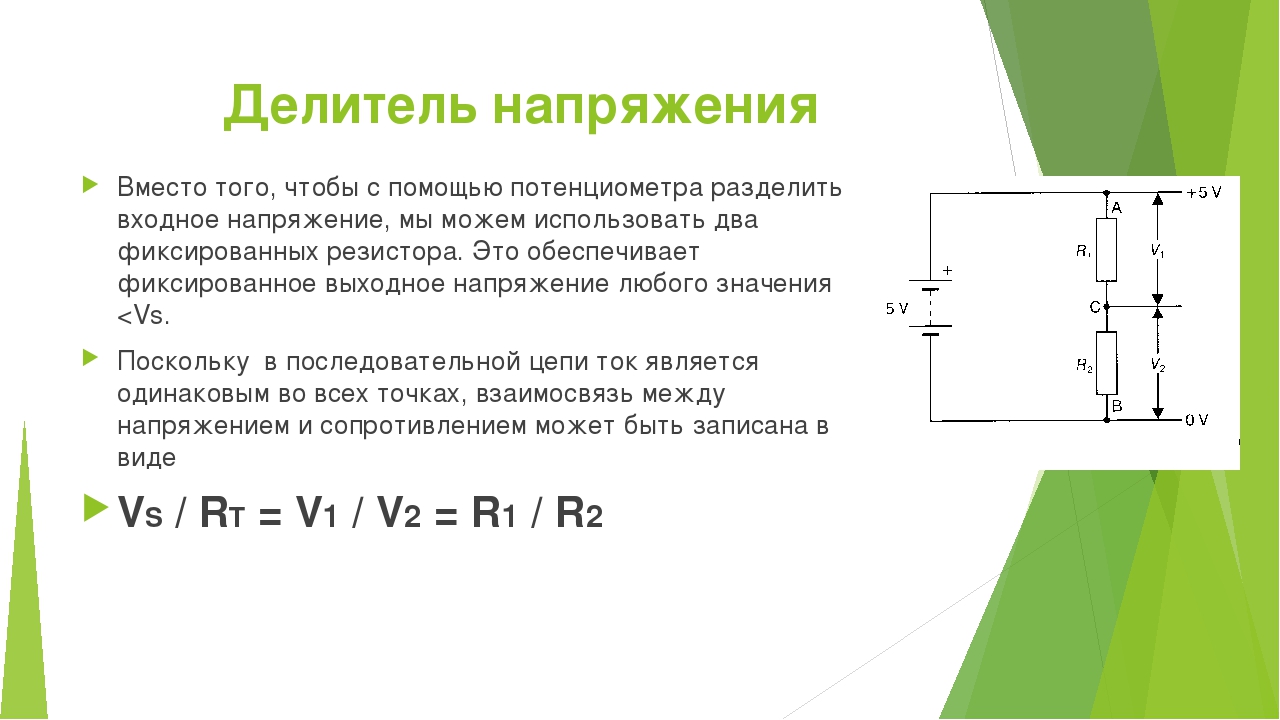
- Результат расчёта
- Назначение и применение
- Расчет резистивного делителя напряжения
- Практическое применение параллельного и последовательного соединения
- Пример работы делителя напряжения на фоторезисторе.
- Потенциометры
- Ограничения в применении
- Расчет резистора для светодиода
- Законы Кирхгофа
- Первый закон
- Второй закон Кирхгофа
- Виды и принцип действия
- Расчет гасящего резистора
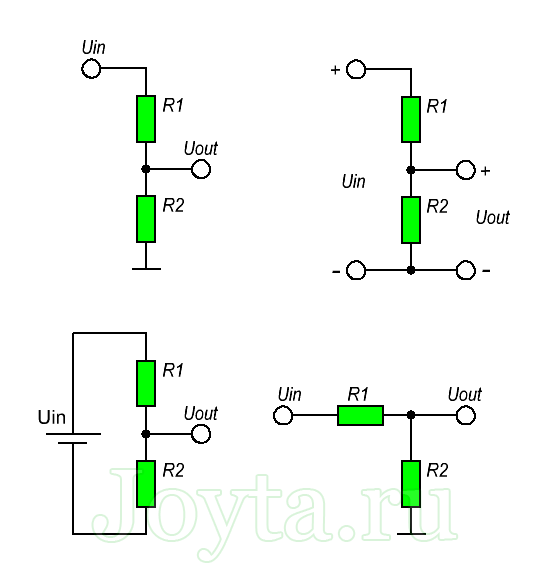
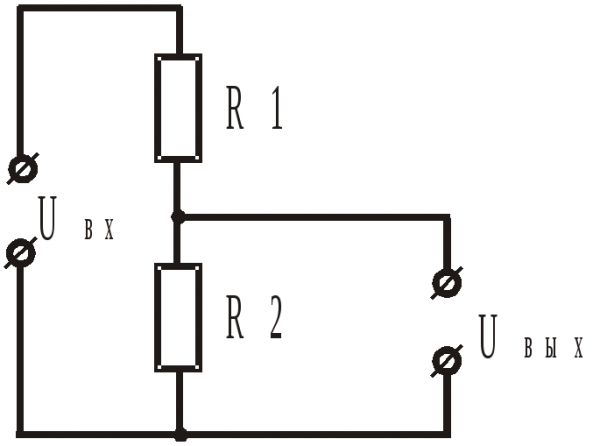
- Схема традиционного резисторного делителя напряжения
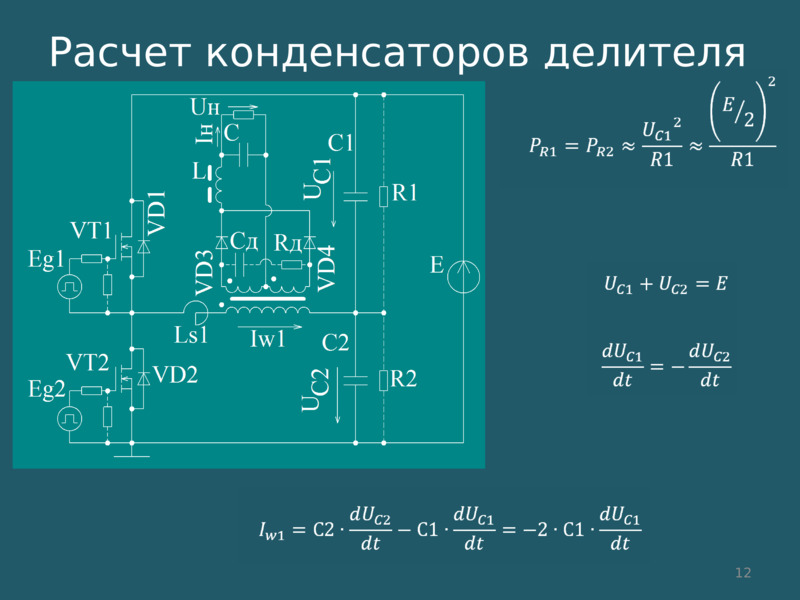
- Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях
- Практическое применение параллельного и последовательного соединения
- Пример работы делителя напряжения на фоторезисторе.
- Потенциометры
- Резистивные датчики
- Резистивный делитель напряжения
- Определение
- Как работает делитель напряжения
- Резистивный делитель напряжения
- Ограничения в применении резистивных делителей напряжения
- Резистивный делитель напряжения
- Расчет делителя напряжения на резисторах
- Формула делителя напряжения
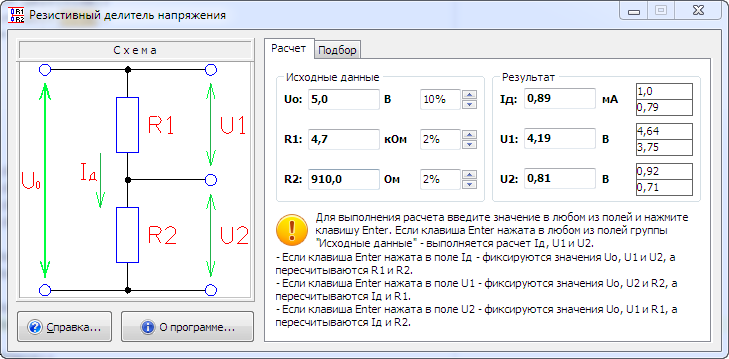
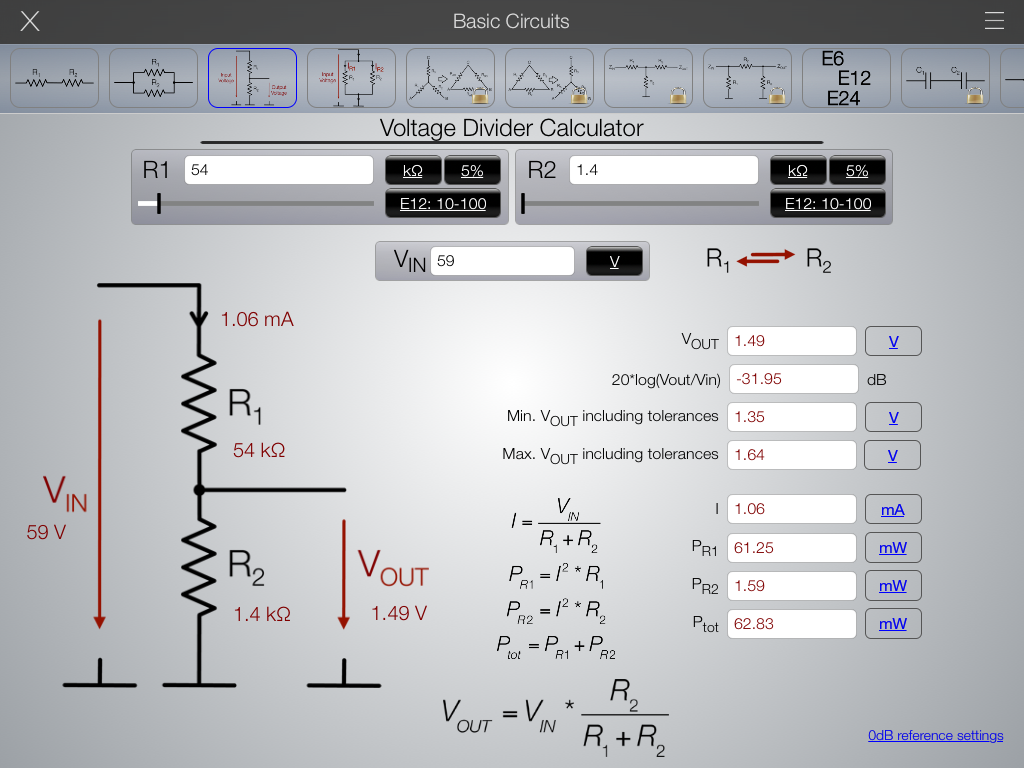
- Расчет делителя напряжения калькулятором онлайн
- Расчёт делителя напряжения
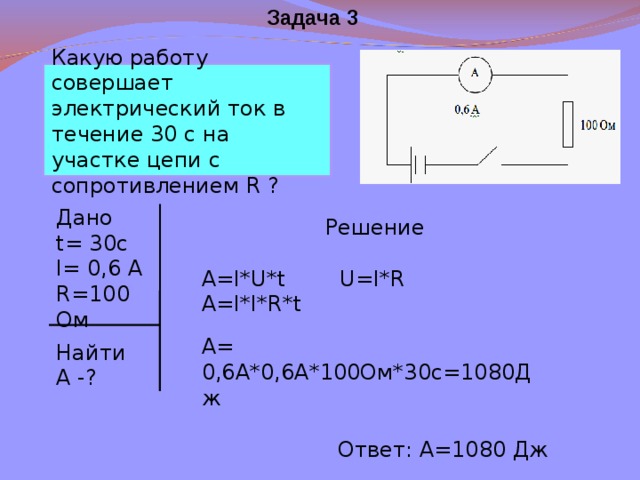
Виды резисторов
Резистор – инертный (пассивный) элемент цепи, у которого сопротивление может быть как постоянным, так и переменным. Это зависит от его конструкции. Он применяется для регулирования силы тока и напряжения в цепях, рассеивания мощности и иных ограничений. Дословный перевод с английского слова «резистор» – сопротивляюсь.
 Общий вид элементов
Общий вид элементов
Классификацию резисторов можно провести по следующим критериям:
- назначение элемента;
- тип изменения сопротивления;
- материал изготовления;
- вид проводника в элементе;
- ВАХ – вольт-амперная характеристика;
- способ монтажа.
Устройства делятся на элементы общего и специального назначения. У специальных деталей повышенные характеристики сопротивления, частоты, рабочего напряжения или особые требования к точности.
Тип изменения сопротивления делит их на постоянные и переменные. Переменные резисторы конструктивно отличаются не только от элементов, имеющих постоянное сопротивление, но и между собой. Они различны по конструкции: бывают регулировочные и подстроечные.
Регулировочные элементы переменного типа предназначены для частого изменения сопротивления. Это входит в процесс работы схемы устройства.
Подстроечный тип предназначен для того, чтобы выполнить подстройку и регулировку схемы при первичном запуске. После этого изменение положения регулятора не выполняют.
При изготовлении резистивных тел (рабочей поверхности) используются такие материалы, как:
- графитовые смеси;
- металлопленочные (окисные) ленты;
- проволока;
- композиционные компоненты.
Особое место занимают в этом ряду интегральные элементы. Это резисторы, выполненные в виде p-n перехода, который представляет собой зигзагообразный канал, интегрируемый в кристалл микросхемы.
Внимание! Интегральные элементы всегда отличаются повышенной нелинейностью своей ВАХ. Поэтому они применяются там, где использование других типов не представляется возможным
Вид вольт-амперной характеристики делит рассматриваемые элементы на линейные и нелинейные. Особенность нелинейности заключается в том, что компонент меняет своё сопротивление в зависимости от следующих характеристик:
- напряжения (варисторы);
- температуры (терморезисторы);
- уровня магнитного поля (магниторезисторы);
- величины освещённости (фоторезисторы);
- коэффициента деформации (тензорезисторы).
Нелинейность вольт-амперной характеристики расширило возможности их применения.
Способ монтажа может быть:
- печатным;
- навесным;
- интегрированным.
При печатном монтаже выводы детали вставляются в отверстие на плате, после чего припаиваются к контактной дорожке панели. Такой способ установки автоматизирован, и пайка происходит путём погружения контактных площадок в ванну с припоем.
Навесной монтаж, в большинстве своём, ручной. Выводы соединяемых деталей сначала скручиваются между собой, потом спаиваются для улучшения контакта. Сама пайка не предназначена для выдерживания механических нагрузок.
Интегрированный монтаж проводится в процессе изготовления кристаллов микросхем.
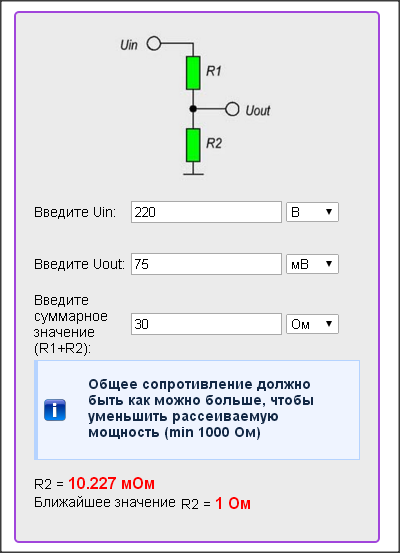
Результат расчёта
 Как правило окажется, что резисторы с таким номиналом не выпускаются, и вам будет показан ближайший стандартный номинал. Если не удаётся сделать точный подбор сопротивления, то используйте больший номинал. Подходящий номинал можно сделать подключая сопротивление параллельно или последовательно. Расчет сопротивления для светодиода можно не делать, если использовать мощный переменный или подстроечный резистор. Наиболее распространены типа 3296 на 0,5W. При использовании питания на 12В, последовательно можно подключить до 3 LED.
Как правило окажется, что резисторы с таким номиналом не выпускаются, и вам будет показан ближайший стандартный номинал. Если не удаётся сделать точный подбор сопротивления, то используйте больший номинал. Подходящий номинал можно сделать подключая сопротивление параллельно или последовательно. Расчет сопротивления для светодиода можно не делать, если использовать мощный переменный или подстроечный резистор. Наиболее распространены типа 3296 на 0,5W. При использовании питания на 12В, последовательно можно подключить до 3 LED.
Резисторы бывают разного класса точности, 10%, 5%, 1%. То есть их сопротивление может погрешность в этих пределах в положительную или отрицательную сторону. Не забываем учитывать и мощность токоограничивающего резистора, это его способность рассеивать определенное количество тепла. Если она будет мала, то он перегреется и выйдет из строя, тем самым разорвав электрическую цепь. Чтобы определить полярность можно подать небольшое напряжение или использовать функцию проверки диодов на мультиметре. Отличается от режима измерения сопротивления, обычно подаётся от 2В до 3В.
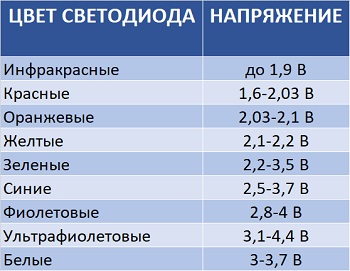 Таблица зависимости рабочего напряжения светодиода от его цвета.
Таблица зависимости рабочего напряжения светодиода от его цвета.
Так же при расчёте светодиодов следует учитывать разброс параметров, для дешевых они будут максимальны, для дорогих они будут более одинаковыми. Чтобы проверить этот параметр, необходимо включить их в равных условиях, то есть последовательно.
Уменьшая тока или напряжение снизить яркость до слегка светящихся точек. Визуально вы сможете оценить, некоторые будут светится ярче, другие тускло. Чем равномернее они горят, тем меньше разброс. Калькулятор расчёта резистора для светодиода подразумевает, что характеристики светодиодных чипов идеальные, то есть отличие равно нулю.
Напряжение падения для распространенных моделей маломощных до 10W может быть от 2В до 12В. С ростом мощности увеличивается количество кристаллов в COB диоде, на каждом есть падение. Кристаллы включаются цепочками последовательно, затем они объединяются в параллельные цепи. На мощностях от 10W до 100W снижение растёт с 12В до 36В. Этот параметр должен быть указан в технических характеристиках LED чипа и зависит от назначения цвета:
- синий;
- красный;
- зелёный;
- желтый;
- трёхцветный RGB;
- четырёхцветный RGBW;
- двухцветный;
- теплый и холодный белый.
 Светодиоды.
Светодиоды.
Прежде чем подобрать резистор для светодиода на онлайн калькуляторе, следует убедится в параметрах диодов. Китайцы на Aliexpress продают множество led, выдавая их за фирменные. Наиболее популярны модели SMD3014, SMD 3528, SMD2835, SMD 5050, SMD5630, SMD5730. Например, чаще всего китайцы обманывают на SMD5630 и SMD5730. Цифры в маркировке обозначают лишь размер корпуса 5,6мм на 3,0мм.
В фирменных такой большой корпус используется для установки мощных кристаллов на 0,5W , поэтому у покупателей диодов СМД5630 напрямую ассоциируется с мощностью 0,5W. Хитрый китаец этим пользуется, и в корпус 5630 устанавливает дешевый и слабенький кристалл в среднем на 0,1W , при этом указывая потребление энергии 0,5W.
Наглядным примером будут автомобильные лампы и светодиодные кукурузы, в которых поставлено большое количество слабеньких и некачественных ЛЕД чипов. Обычный покупатель считает, чем больше светодиодов чем лучше светит и выше мощность. Автомобильные лампы на самых слабых лед 0,1W Чтобы сэкономить денежку, мои светодиодные коллеги ищут приличные ЛЕД на Aliexpress. Ищут хорошего продавца, который обещает определённые параметры, заказывают , ждут доставку месяц. После тестов оказывается, что китайский продавец обманул, продал барахло. Повезёт, если на седьмой раз придут приличные диоды, а не барахло. Обычно сделают 5 заказов, и не добившись результата и идут делать заказ в отечественный магазин, который может сделать обмен.
Назначение и применение
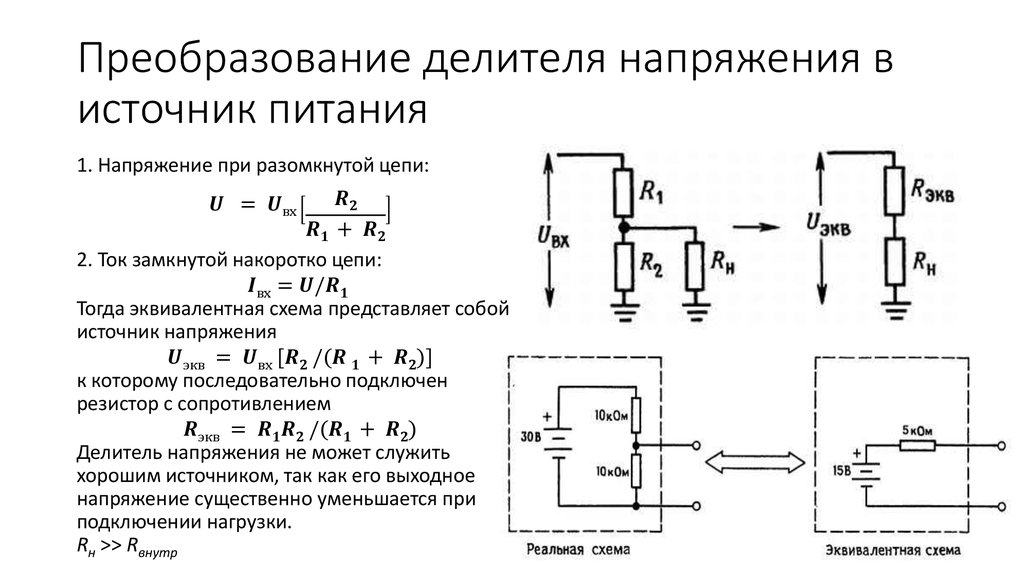
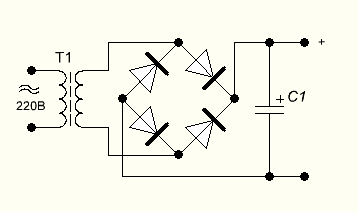
Для преобразования переменного напряжения применяется трансформатор, благодаря которому можно сохранить достаточно высокое значение тока. Если необходимо в электрическую цепь подключить нагрузку, потребляющую небольшой ток (до сотен мА), то использование трансформаторного преобразователя напряжения (U) не является целесообразным.
В этих случаях можно использовать простейший делитель напряжения (ДН), стоимость которого существенно ниже. После получения необходимой величины U выпрямляется и происходит подача питания на потребитель. При необходимости для увеличения силы тока (I) нужно использовать выходной каскад увеличения мощности. Кроме того, существуют делители и постоянного U, но эти модели применяются реже остальных.
ДН часто применяются для зарядок различных устройств, в которых нужно получить из 220 В более низкие значения U и токов для разного типа аккумуляторов. Кроме того, целесообразно использовать устройства для деления U для создания электроизмерительных приборов, компьютерной техники, а также лабораторных импульсных и обыкновенных блоков питания.
 Watch this video on YouTube
Watch this video on YouTube
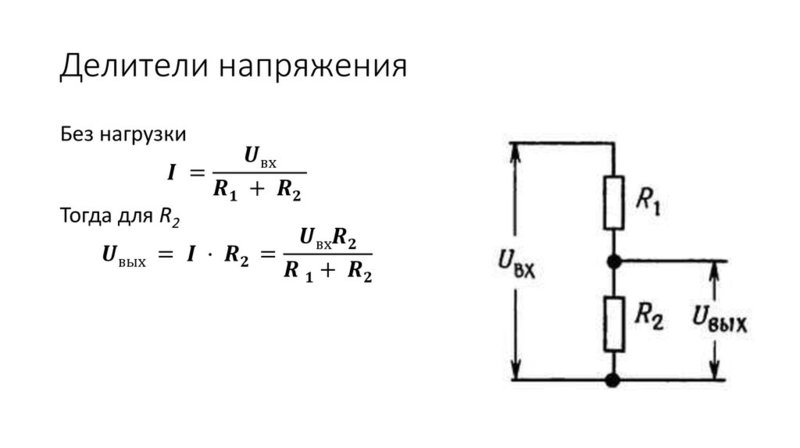
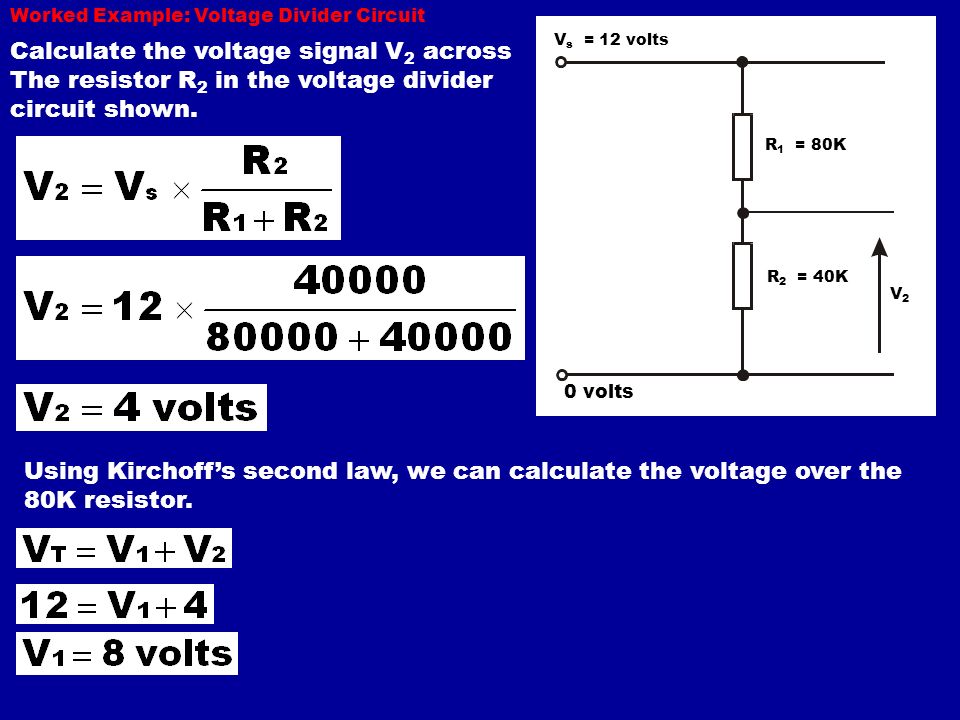
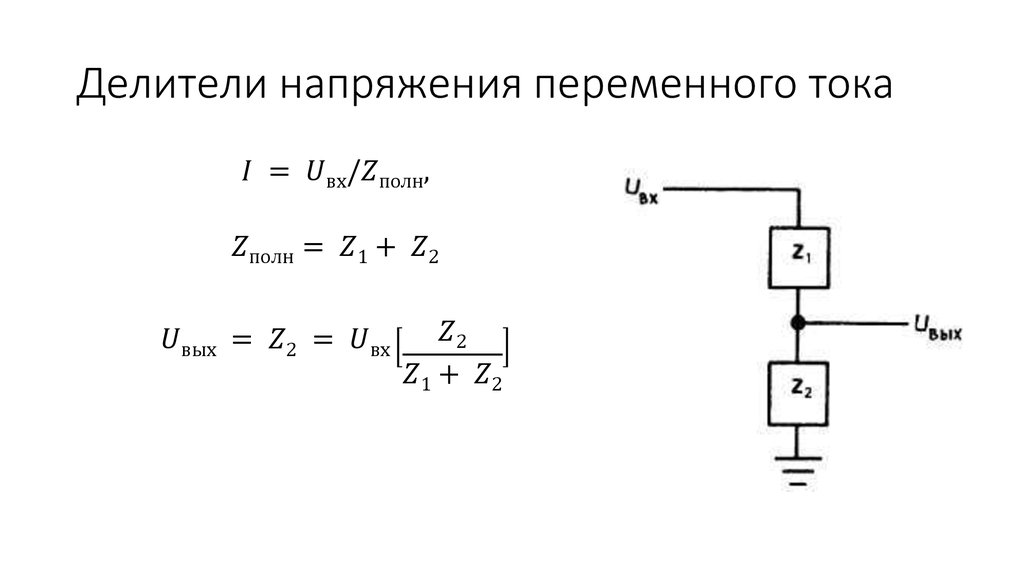
Расчет резистивного делителя напряжения
[Напряжение на выходе, В] = [Напряжение питания, В] * [Сопротивление резистора R2, Ом] / ([Сопротивление резистора R1, Ом] + [Сопротивление резистора R2, Ом])
Из этой формулы, в частности, видно, что резисторные (резистивные) делители выдают стабильное выходное напряжение, если напряжение питания фиксировано.
[Входное сопротивление делителя, Ом] = [Сопротивление резистора R1, Ом] + [Сопротивление резистора R2, Ом]
Эта формула верна для ненагруженного делителя. Если делитель работает на нагрузку, то [Входное сопротивление делителя, Ом] = [Сопротивление резистора R1, Ом] + 1 / (1 / [Сопротивление резистора R2, Ом] + 1 / [Сопротивление нагрузки, Ом])
[Эквивалентное выходное сопротивление делителя, Ом] = 1 / (1 / [Сопротивление резистора R1, Ом] + 1 / [Сопротивление резистора R2, Ом])
[Коэффициент ослабления сигнала] = [Сопротивление резистора R2, Ом] / ([Сопротивление резистора R1, Ом] + [Сопротивление резистора R2, Ом])
[Действующее / мгновенное / амплитудное напряжение на выходе делителя, В] = [Коэффициент ослабления сигнала] * [Действующее / мгновенное / амплитудное напряжение на входе делителя, В]
Эта формула верна, если ток нагрузки делителя равен нулю.
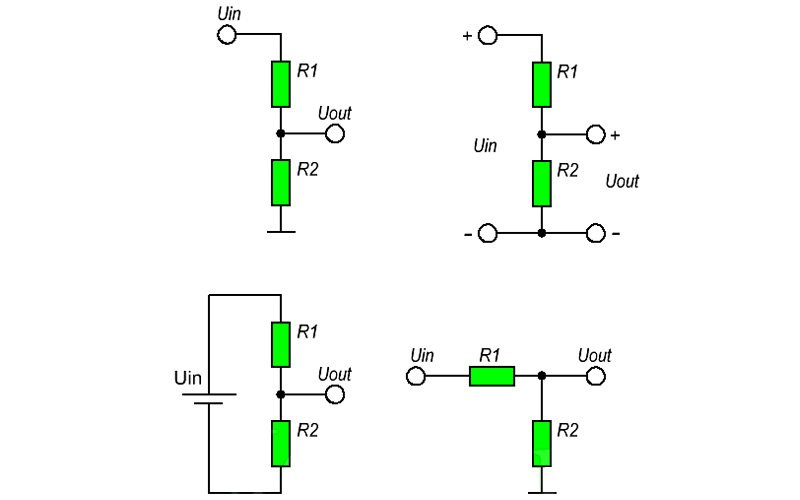
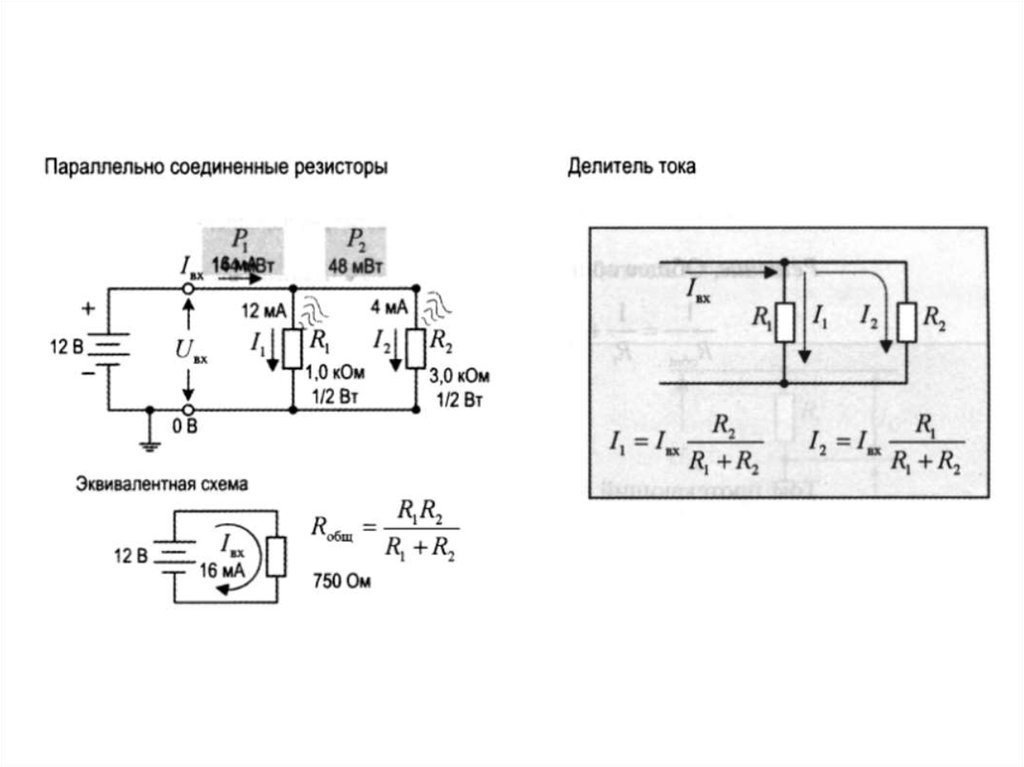
Практическое применение параллельного и последовательного соединения
Составные элементы прибора соединяют в цепь, чтобы получить из сети нужную для устройства часть энергии.
Пример работы делителя напряжения на фоторезисторе.
Исходное сопротивление меняется от 1кОм в момент полного освещения до 10кОм при отсутствии света, то можно увеличить диапазон сопротивления. При добавлении резисторов с R=5,6кОм, исходящее напряжение меняется следующим образом:
| Освещённость | R1 (кОм) | R2(кОм) | R2/(R1+R2) | U выходное (В) |
| Яркая | 5,6 | 1 | 0,15 | 0,76 |
| Тусклая | 5,6 | 7 | 0,56 | 2,78 |
| Темнота | 5,6 | 10 | 0,67 | 3,21 |
Таким образом, увеличивается диапазон выходного напряжения, и оно становится подходящим для большинства сетей.
Потенциометры
Потенциометры используют в качестве делителя в системе с постоянным током. Их применяют в основном для изменения отдельных параметров в механизме.

Ограничения в применении
Из приведенных в таблице примеров расчетов хорошо видно, как значительно увеличиваются потери при уменьшении сопротивления цепи. Энергия расходуется впустую для нагрева окружающей среды. При большой мощности рассеивания приходится использовать принудительные системы охлаждения, пассивные радиаторы.
В приведенных расчетах не учитывалась нагрузка. Если добавить соответствующее реальным условиям сопротивление, образуются дополнительные потери в параллельной цепи.
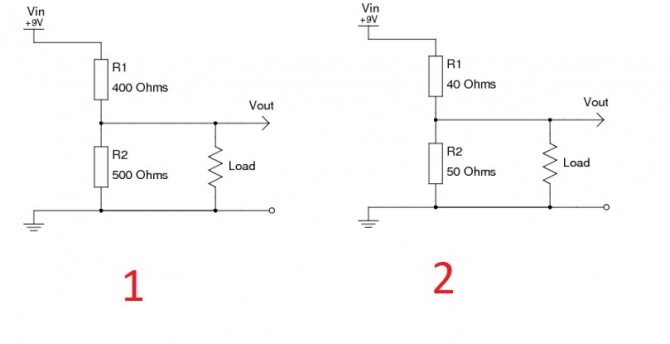
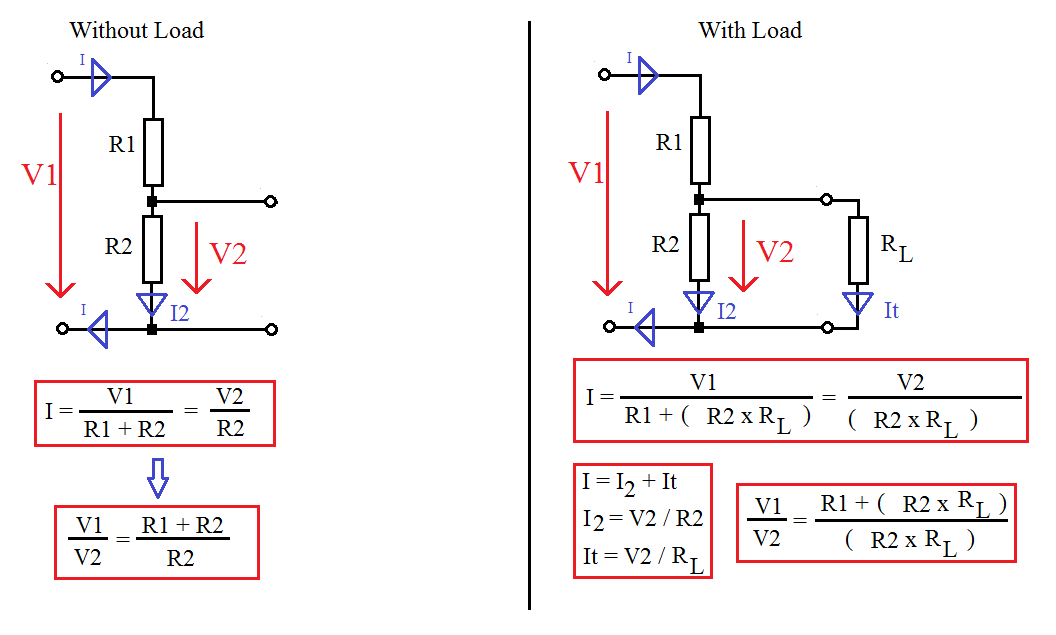
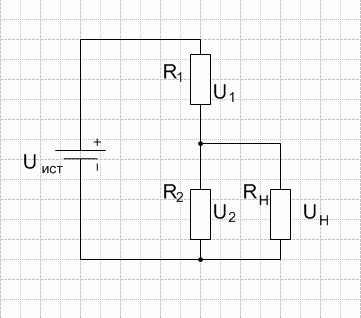
Влияние сопротивления нагрузки
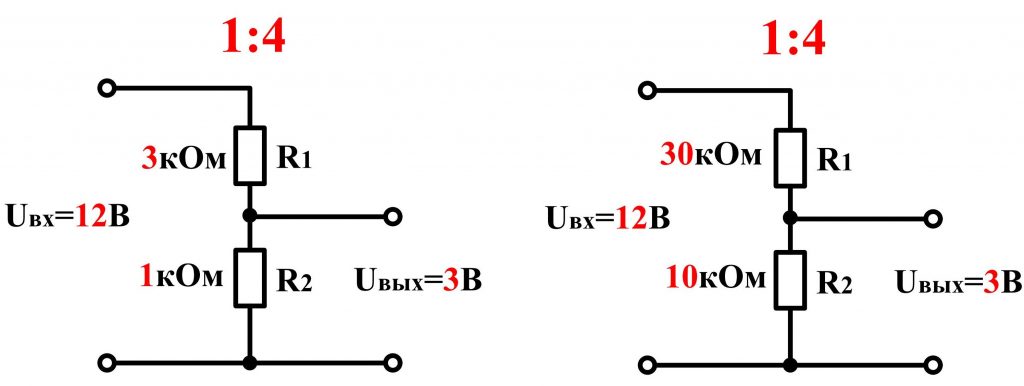
На первой части рисунка изображен типовой делитель, обеспечивающий выходное напряжение 5 V. При потреблении тока 0,01 А сопротивление нагрузки составит 0,5 кОм. Пользуясь формулой расчета для параллельной цепи, несложно выяснить суммарное значение R = 1/(1/R2 + 1/Rнагрузки) = 0,25 кОм. Это добавление уменьшит плановое значение Uвых до 3,46 V.
Уменьшением R2 можно снизить вредное влияние на выходное напряжение (4,75 V). Однако такой способ, приведенный на второй части рисунка, сопровождается значительными потерями энергии. Ток будет проходить по участку с меньшим сопротивлением, не выполняя полезные функции. В данном примере необходимо выбрать R1, рассчитанный на мощность не менее 2 Вт, чтобы обеспечить надежную работу устройства.
Расчет резистора для светодиода
Сопротивление балластного резистора легко рассчитать, используя закон Ома и правила Кирхгофа. Чтобы рассчитать необходимое сопротивление резистора, нам необходимо из напряжения источника питания вычесть номинальное напряжение светодиода, а затем эту разницу разделить на рабочий ток светодиода:
где:
- V — напряжение источника питания
- VLED — напряжение падения на светодиоде
- I – рабочий ток светодиода
Ниже представлена таблица зависимости рабочего напряжения светодиода от его цвета:

Умный ПДУ для светодиодной лентыКонтроллер для RGBW/RGB/Dual White. Управление по радиоканалу, WIFI…

Светодиодный драйвер на PT4115Для светодиодов 3 Вт 700mA / 1 Вт 350mA

Инфракрасный включатель для светодиодной лентыНапряжение: 12/24В, ток: 5А, расстояние срабатыва…

Драйвер для светодиодной ленты220В/12В, мощность: 18 Вт / 36 Вт / 72 Вт / 100 Вт…

Светодиодный драйверМощность: 3 Вт, 4 Вт, 5 Вт, 7 Вт, Напряжение: 3…12В, выходной ток…

Контроллер светодиодной лентыBluetooth — WiFi контроллер для 5050, WS2811, WS2812B сведодиодной ленты…
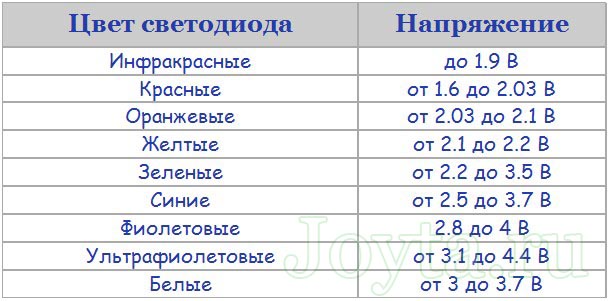
Хотя эта простая схема широко используется в бытовой электронике, но все же она не очень эффективна, так как избыток энергии источника питания рассеивается на балластном резисторе в виде тепла. Поэтому, зачастую используются более сложные схемы (драйверы для светодиодов) которые обладают большей эффективностью.
Давайте, на примере выполним расчет сопротивления резистора для светодиода.
Мы имеем:
- источник питания: 12 вольт
- напряжение светодиода: 2 вольта
- рабочий ток светодиода: 30 мА
Рассчитаем токоограничивающий резистор, используя формулу:
Получается, что наш резистор должен иметь сопротивление 333 Ом. Если точное значение из номинального ряда резисторов подобрать не получается, то необходимо взять ближайшее большее сопротивление. В нашем случае это будет 360 Ом (ряд E24).
Законы Кирхгофа
Первый закон
Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два. Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю. Если посмотреть на схему, I1 — это ток, который заходит в узел, I2 и I3 — это электроны, которые вытекают из него. Применяя формулировку первого закона можно записать формулу по-другому: I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.
Второй закон Кирхгофа
Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре.
Виды и принцип действия
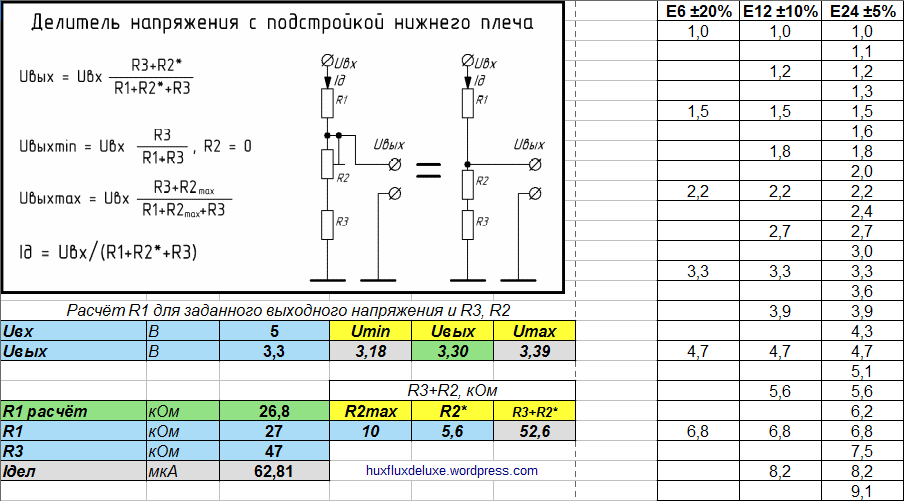
В данной публикации подробно рассмотрен резистивный делитель напряжения. Подразумевается линейность характеристики цепи. В таких схемах упрощен расчет сопротивления для понижения напряжения до необходимого уровня. При подключении источника постоянного тока происходит деление напряжений прямо пропорционально значениям электрических сопротивлений нижнего и верхнего плеча.
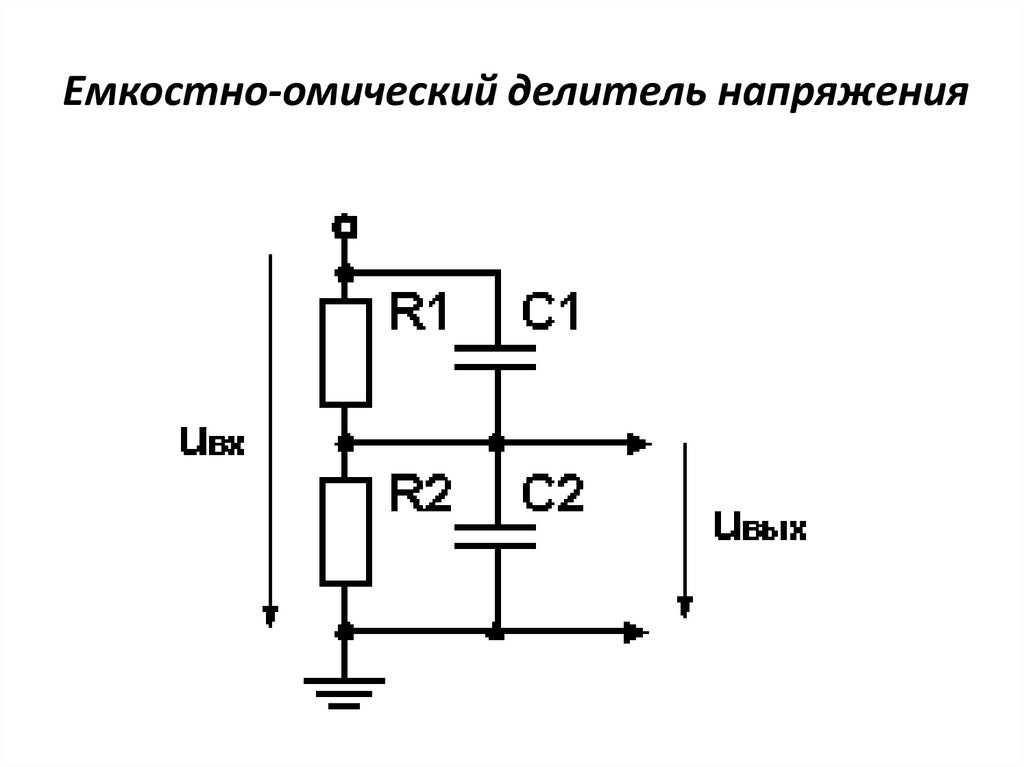
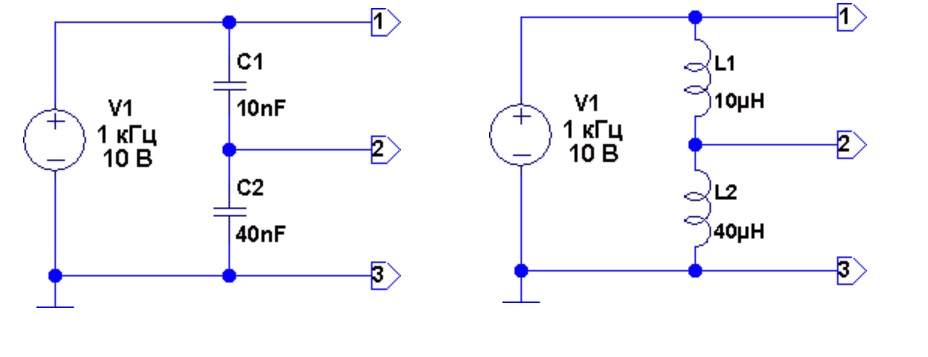 Цепи с реактивными характеристиками
Цепи с реактивными характеристиками
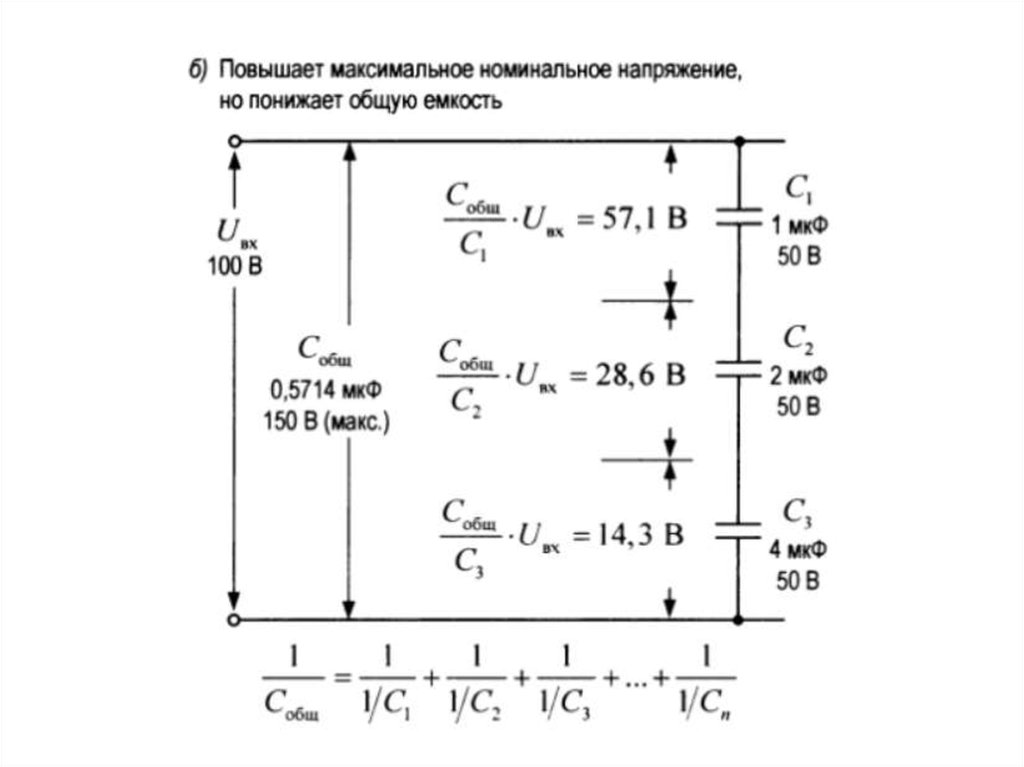
Если составить аналогичную схему с конденсаторами, то на вход для поддержания нормальной функциональности придется подать синусоиду. В этом случае также будет выполнено распределение напряжений на элементах с емкостными характеристиками. Однако этот процесс надо рассматривать в динамике, с учетом частоты и соответствующего изменения амплитуды. Аналогичную методику применяют при работе с индуктивными компонентами.
Значения реактивных сопротивлений:
- Rc=1/(2*f*π*C);
- RL=2*f*π*C.
По формулам видно, что сопротивление конденсатора/ катушки обратно (прямо) пропорционально емкости/ индуктивности. Соответственно выбирают значения элементов для деления напряжения.
В представленных примерах принимают бесконечно большим внутреннее сопротивление нагрузки. Для реальных расчетов пользуются более сложными формулами с поправочными коэффициентами. Учитывают действительные комплексные характеристики цепей.
К сведению. В стабилизаторах напряжения и некоторых иных устройствах сопротивление плеча делителя обладает нелинейными параметрами.
Расчет гасящего резистора
В схемах аппаратуры связи часто возникает необходимость подать на потребитель меньшее напряжение, чем дает источник. В этом случае последовательно с основным потребителем включают дополнительное сопротивление, на котором гасится избыток напряжения источника. Такое сопротивление называется гасящим.
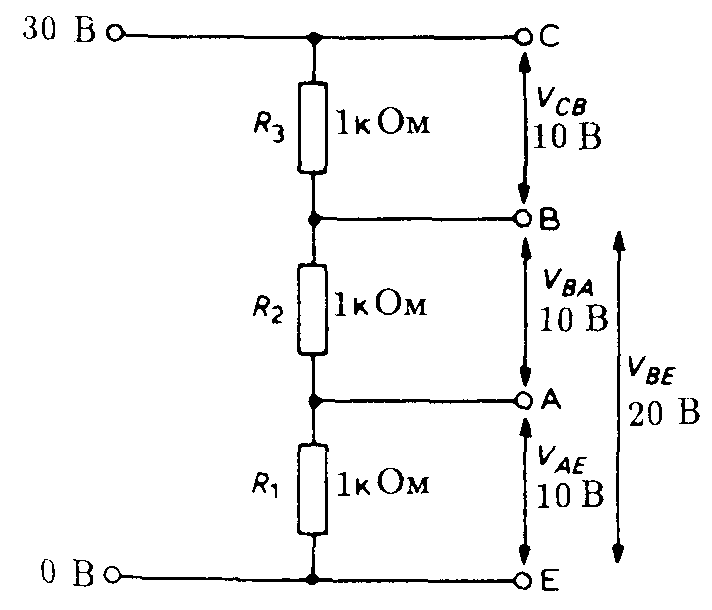
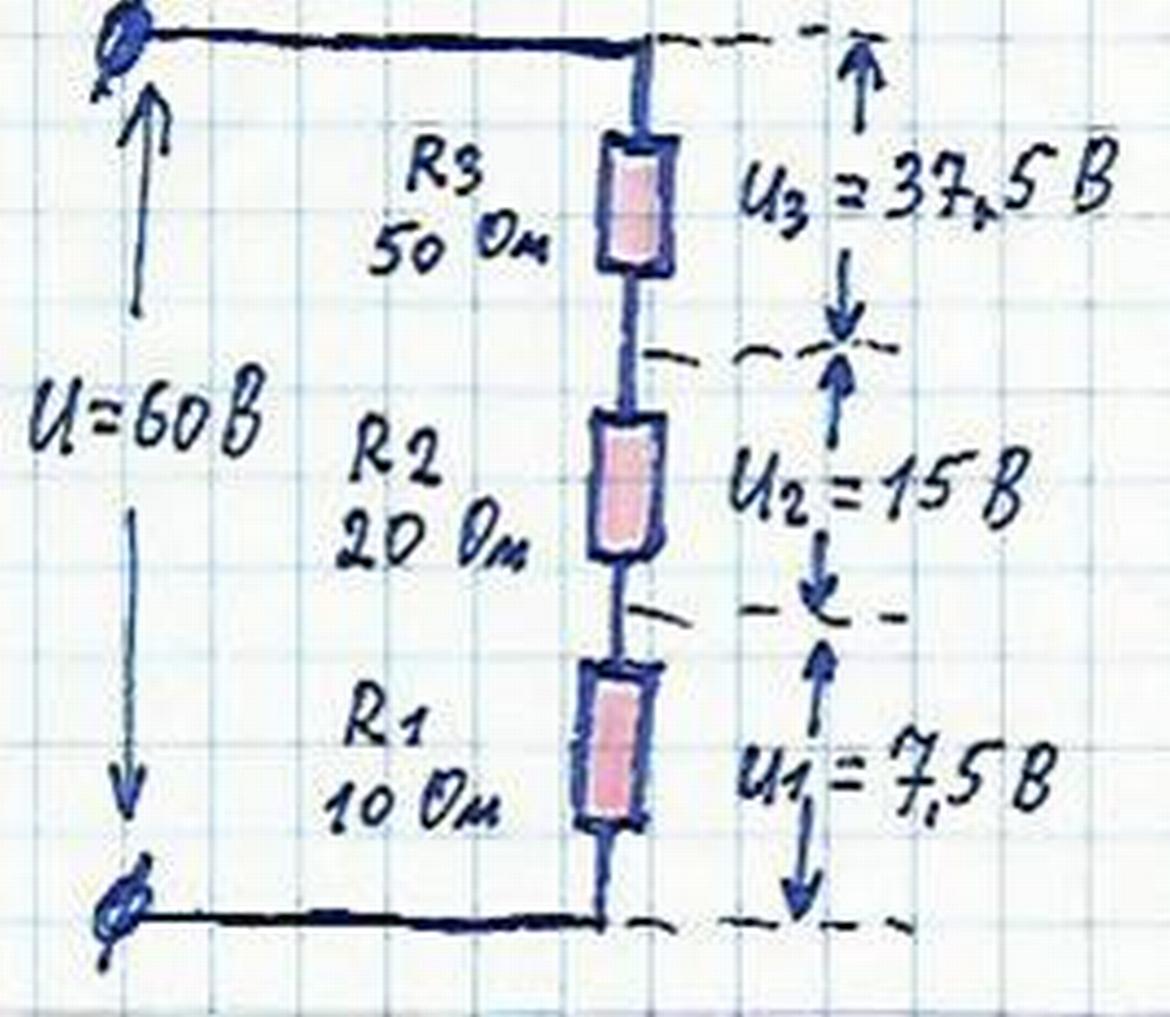
Напряжение источника тока распределяется по участкам последовательной цепи прямо пропорционально сопротивлениям этих участков. Рассмотрим схему включения гасящего сопротивления:
- Полезной нагрузкой в этой цепи является лампочка накаливания, рассчитанная на нормальную работу при величине напряжения Uл= 80 в и тока I =20 ма.
- Напряжение на зажимах источника тока U=120 в больше Uл, поэтому если подключить лампочку непосредственно к источнику, то через нее пройдет ток, превышающий нормальный, и она перегорит.
- Чтобы этого не случилось, последовательно с лампочкой включено гасящее сопротивление R гас.
Схема включения гасящего сопротивления резистора.
Расчет величины гасящего сопротивления при заданных значениях тока и напряжения потребителя сводится к следующему:
– определяется величина напряжения, которое должно быть погашено:
Uгас = Uист – Uпотр,
Uгас = 120 – 80 = 40в
определяется величина гасящего сопротивления
Rгас = Uгас / I
Rгас = 40 / 0,020 = 2000ом = 2 ком
Далее необходимо рассчитать мощность, выделяемую на гасящем сопротивлении по формуле
P = I2 * Rгас
P = 0,0202 * 2000 = 0,0004 * 2000 = 0,8вт
Зная величину сопротивления и расходуемую мощность, выбирают тип гасящего сопротивления.
Схема традиционного резисторного делителя напряжения
Для применения делителя напряжения нам надо уметь рассчитывать три величины: напряжение на выходе делителя, его эквивалентное выходное сопротивление, его входное сопротивление. С напряжением все понятно. Эквивалентное выходное сопротивление скажет нам, насколько изменится напряжение на выходе с изменением тока нагрузки делителя. Если эквивалентное выходное сопротивление равно 100 Ом, то изменение тока нагрузки на 10 мА приведет к изменению напряжения на выходе на 1 В. Входное сопротивление показывает, насколько делитель нагружает источник сигнала или источник питания. Дополнительно посчитаем коэффициент ослабления сигнала. Он может пригодиться при работе с сигналами сложной формы.
Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях
Делитель на резисторах — отличается своей универсальностью: используют при постоянном и переменном токе, но только при пониженном сопротивлении цепи.
Тогда на каждом из резисторов: U1= I х R1 и U2 = I х R2 Ток в цепи устройства:
Уменьшение на конденсаторах применяют для цепей с высоким переменным током. В нём минимальная потеря энергии на выходе. Реактивное сопротивление конденсатора зависит от его электроёмкости и частоты напряжения в цепи.
Формула для вычисления сопротивления:
Делитель на индуктивностях используется при переменном низком токе на высоких частотах. Сопротивление катушки переменного тока прямо пропорционально зависит от индуктивности и частоты. У провода катушки имеется активное сопротивление, из-за чего мощность такого прибора больше, чем у аналогов.
Сопротивление катушки находится по формуле:
Практическое применение параллельного и последовательного соединения
Составные элементы прибора соединяют в цепь, чтобы получить из сети нужную для устройства часть энергии.
Пример работы делителя напряжения на фоторезисторе.
Исходное сопротивление меняется от 1кОм в момент полного освещения до 10кОм при отсутствии света, то можно увеличить диапазон сопротивления. При добавлении резисторов с R=5,6кОм, исходящее напряжение меняется следующим образом:
| Освещённость | R1 (кОм) | R2(кОм) | R2/(R1+R2) | U выходное (В) |
| Яркая | 5,6 | 1 | 0,15 | 0,76 |
| Тусклая | 5,6 | 7 | 0,56 | 2,78 |
| Темнота | 5,6 | 10 | 0,67 | 3,21 |
Таким образом, увеличивается диапазон выходного напряжения, и оно становится подходящим для большинства сетей.
Потенциометры
Потенциометры используют в качестве делителя в системе с постоянным током. Их применяют в основном для изменения отдельных параметров в механизме.
На потенциометр подается напряжение, регулируемое подвижным контактом, который действует, когда крутят ручку, в результате оно может меняться от нуля до исходного значения.Потенциометры используют в быту, как регулятор громкости, и в электронике, например, в качестве датчика.
Резистивные датчики
Резистивные датчики также называют омическими. Это приборы, в которых изменяется сопротивление, если изменяется длина, площадь сечения или удельное сопротивление. Их используют в устройствах для изменения сопротивления, а также при помощи микроконтроллера с его помощью вы можете измерить напряжение. Существуют различные датчики, одним из некоторых является фоторезистор — переменный резистор, сопротивление которого зависит от попадающего на него света.
Резистивный делитель напряжения
В общем случае устройства этого типа выполняют преобразование по формуле Uвых=Uвх*К, где:
- Uвх (вых) – напряжения на входе и выходе, соответственно;
- К – корректирующий множитель, обозначающий передающие способности узла.
Если взять первый пример из рис. выше, для уточнения сути процессов подойдет второй закон Кирхгофа. В соответствии с этим правилом, общее значение напряжений на последовательно соединенных резисторах будет равно сумме ЭДС на каждом элементе. Так как ток не изменяется в замкнутом контуре, для расчета можно использовать закон Ома:
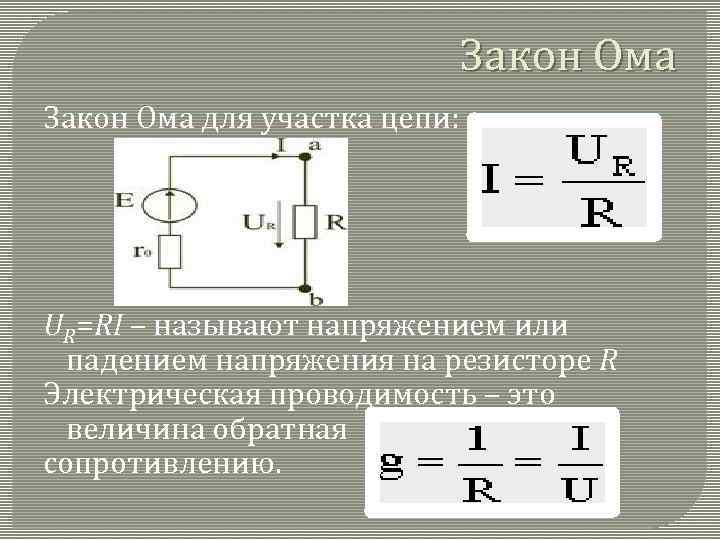
U (напряжение) = I (ток) * R (электрическое сопротивление)
Нижнюю часть схемы (плечо) используют для получения необходимого изменения входного параметра.
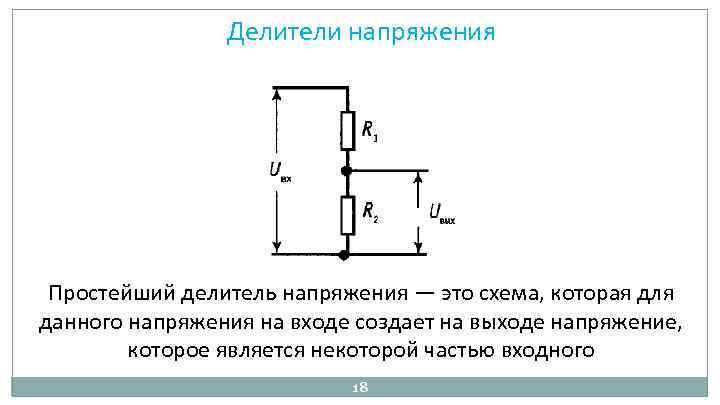
Определение
Делителем напряжения называется прибор или устройство, которое понижает уровень выходного напряжения относительно входного, пропорционально коэффициенту передачи (он будет всегда ниже нуля). Такое название он получил, потому что представляет собой два и более последовательно соединенных участка цепи.
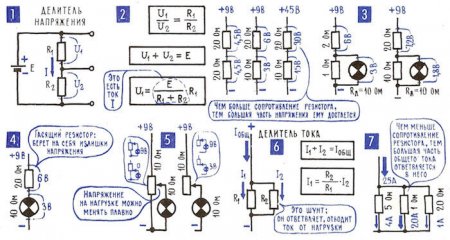
Они бывают линейными и нелинейными. При этом первые представляют собой активное или реактивное сопротивление, в которых коэффициент передачи определяется соотношением из закона Ома. К ярко выраженным нелинейным делителям относят параметрические стабилизаторы напряжения. Давайте разберемся как устроен это прибор и зачем он нужен.
Как работает делитель напряжения
Основной функцией делителя напряжения в электрических цепях является снижение напряжения и получение нескольких его значений с фиксированными показателями на различных участках. Его основой служат резисторы или реактивные сопротивления в количестве два и более элементов.
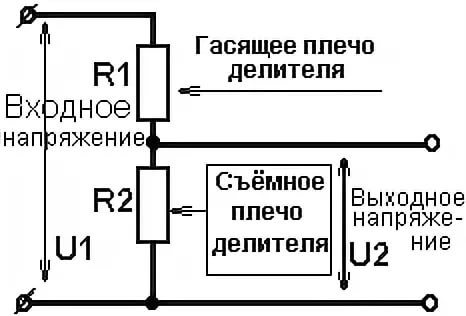
Простейший делитель представляется в виде двух участков цепи, называемых плечами. Верхним плечом считается участок между нулевой точкой и положительным напряжением, а нижним – участок между нулевой точкой и минусом. После того как определены исходные данные, можно сделать самый простой расчет делителя напряжения.
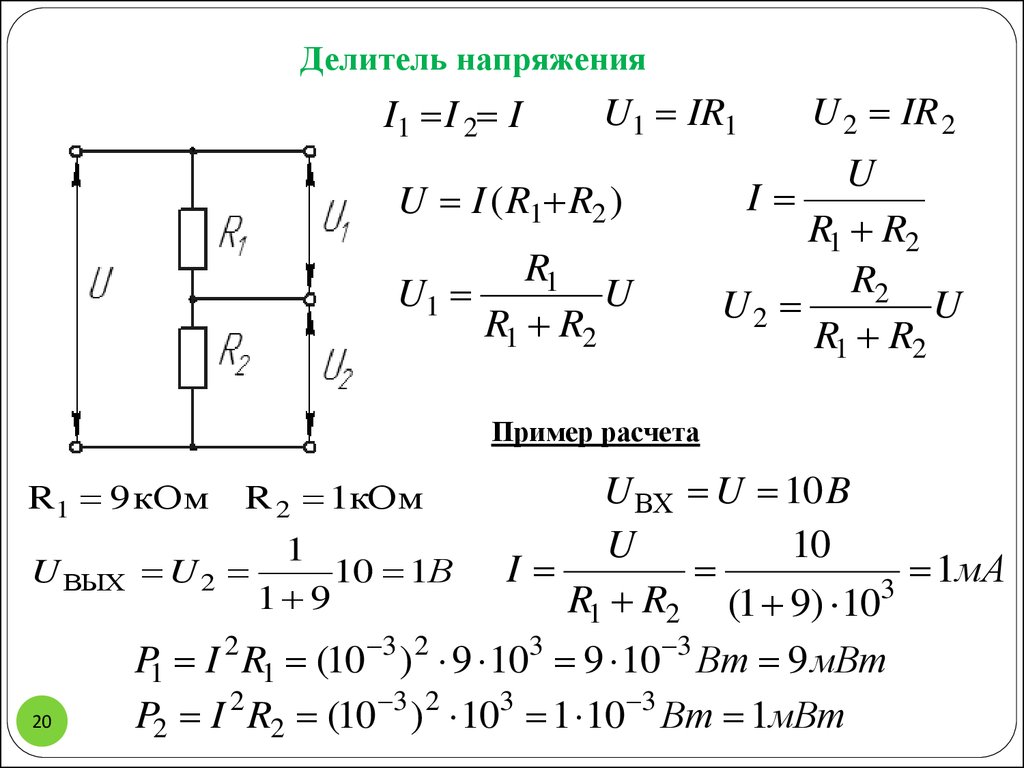
В качестве примера рассматриваются два резистора, соединенные последовательно. К ним подается напряжение U, которое может быть переменными или постоянным. После этого в действие вступает закон Ома, когда при последовательном соединении резисторов, общее сопротивление составит сумму их номиналов. В виде формы это будет выглядеть следующим образом: I = U/Rобщ, в которой Rобщ = R1+R2. Следовательно, I = U/(R1+R2).
Сила тока при последовательно соединенных резисторов, будет одинаковой на всех участках цепи. Если у каждого резистора имеется собственное значение сопротивления, то по закону Ома у них образуются совершенно разные напряжения. Сопротивлению R1 соответствует напряжение U1, а сопротивлению R2 – напряжение U2. В результате получается следующая ситуация, выраженная формулой I = U2/R2 = U1/R1 = U/(R1+R2).
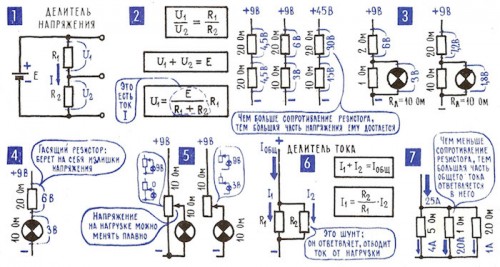
Для того, чтобы найти значения напряжений U1 и U2, необходимо выполнить такие действия: U1 = U x R1/(R1+R2) и U2 = U x R2/(R1+R2). Если правые части каждого уравнения сложить друг с другом, то в результате получится значение входящего напряжения U, состоящее из суммы напряжений U1 и U2, то есть U = U1 + U2. Это значит, что сумма падений напряжений на всех последовательно соединенных резисторах, будет равна напряжению источника питания, то есть входящему напряжению. Таким образом, данное выражение есть ни что иное, как формула делителя напряжения. Практически получается, что входящее напряжение U оказалось разделенным на два напряжения с собственными значениями – U1 и U2.
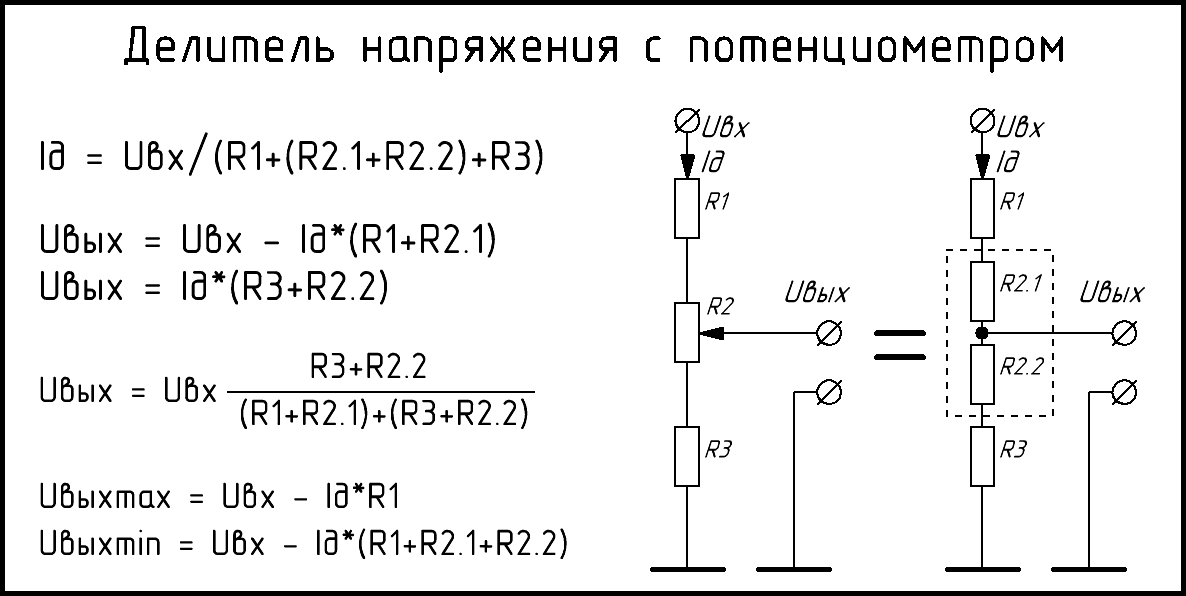
Во многих случаях необходимо, чтобы процесс разделения напряжения осуществлялся плавно. С этой целью был изобретен прибор – переменный резистор. Работа устройства происходит по установленной схеме. Два крайних контакта обладают постоянным сопротивлением, а сопротивление среднего контакта относительно крайних контактов будет изменяться в зависимости от направления вращения регулятора. С помощью переменных резисторов добавляется громкость в звуковых колонках, у радиоприемников и телевизоров старых марок.
Резистивный делитель напряжения
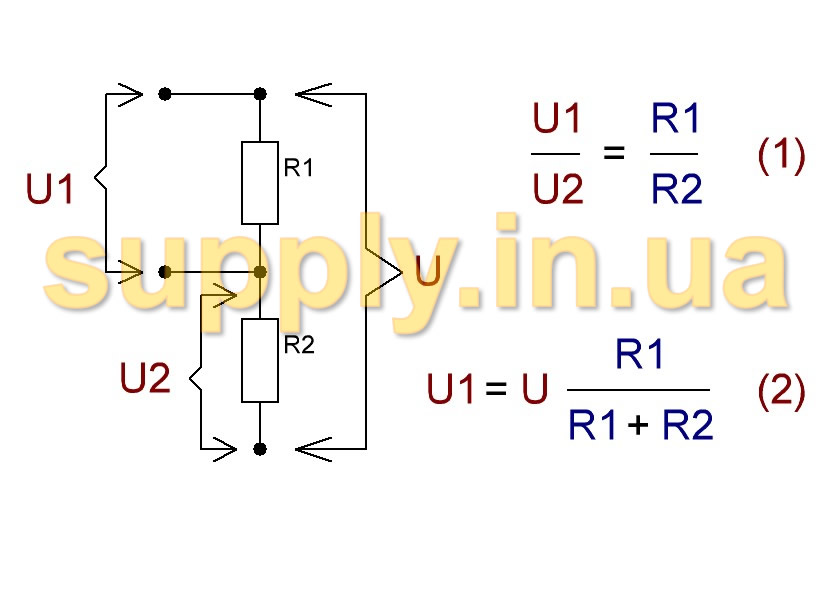
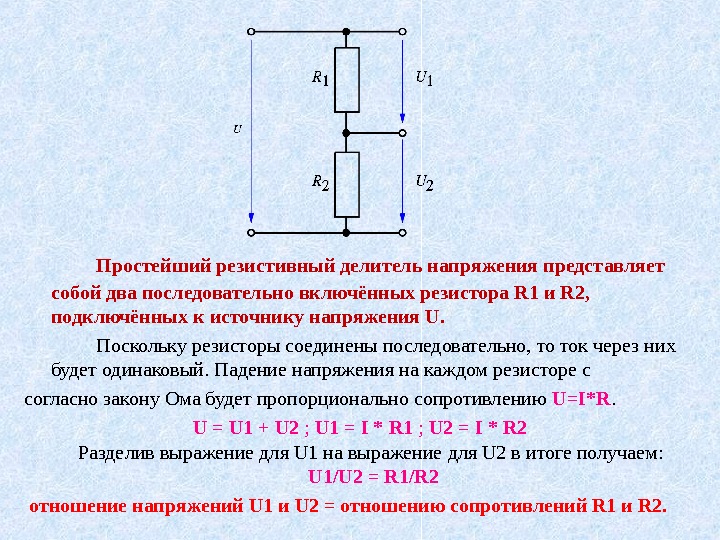
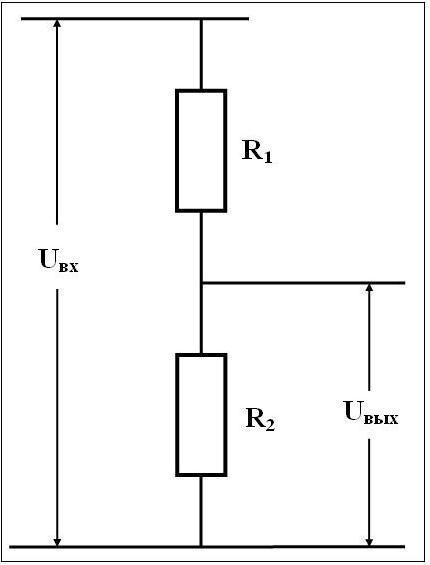
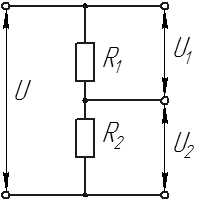
Схема простейшего резистивного делителя напряжения
Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения U{\displaystyle U}. Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
U=IR{\displaystyle \ U=IR}.
Для каждого резистора имеем:
{U1=IR1U2=IR2.{\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}\\U_{2}=IR_{2}.\end{array}}\right.}
Сложив выражения, получаем:
U1+U2=I(R1+R2).{\displaystyle U_{1}+U_{2}=I(R_{1}+R_{2}).}
Далее:
I=U1+U2R1+R2=UR1+R2.{\displaystyle I={\frac {U_{1}+U_{2}}{R_{1}+R_{2}}}={\frac {U}{R_{1}+R_{2}}}.}
Из этого следует:
{U1=IR1=UR1R1+R2U2=IR2=UR2R1+R2.{\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}=U{\frac {R_{1}}{R_{1}+R_{2}}}\\U_{2}=IR_{2}=U{\frac {R_{2}}{R_{1}+R_{2}}}.\end{array}}\right.}
Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно R2{\displaystyle R_{2}}, можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму
Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U{\displaystyle U}. Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R=R1+R2{\displaystyle R=R_{1}+R_{2}}. Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.
Ограничения в применении резистивных делителей напряжения
Для обеспечения приемлемой точности работы делителя требуется проектировать его таким образом, чтобы величина тока, протекающего через цепи делителя, была не менее чем в 10 раз больше, нежели ток, протекающий через нагрузку. Увеличение этого соотношения до ×100, ×1000 и более при прочих равных условиях пропорционально повышает точность работы делителя. Таким же образом, вообще говоря, должны соотноситься и величины сопротивлений делителя и нагрузки. Нетрудно видеть, что идеальным (с точки зрения КПД) режимом работы делителя, является режим т.н. холостого хода, т.е. режим работы при отключенной нагрузке, когда её свойствами можно пренебречь. Увеличение тока нагрузки приводит к существенному падению КПД делителя, из-за того, что существенная часть мощности тратится на нагрев резисторов делителя. Вот почему резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы. Для решения этой задачи используют другие схемотехнические решения, в частности применяют стабилизаторы напряжения. Если же не требуется большой мощности, но требуется исключительно высокая точность поддержания величины выходного напряжения, то используют разнообразные источники опорного напряжения.
Резистивный делитель напряжения
Схема простейшего резистивного делителя напряжения
Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения U{\displaystyle U}. Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
U=IR{\displaystyle \ U=IR}.
Для каждого резистора имеем:
{U1=IR1U2=IR2.{\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}\\U_{2}=IR_{2}.\end{array}}\right.}
Сложив выражения, получаем:
U1+U2=I(R1+R2).{\displaystyle U_{1}+U_{2}=I(R_{1}+R_{2}).}
Далее:
I=U1+U2R1+R2=UR1+R2.{\displaystyle I={\frac {U_{1}+U_{2}}{R_{1}+R_{2}}}={\frac {U}{R_{1}+R_{2}}}.}
Из этого следует:
{U1=IR1=UR1R1+R2U2=IR2=UR2R1+R2.{\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}=U{\frac {R_{1}}{R_{1}+R_{2}}}\\U_{2}=IR_{2}=U{\frac {R_{2}}{R_{1}+R_{2}}}.\end{array}}\right.}
Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно R2{\displaystyle R_{2}}, можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму
Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U{\displaystyle U}. Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R=R1+R2{\displaystyle R=R_{1}+R_{2}}. Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.
Расчет делителя напряжения на резисторах
Удельное сопротивление меди
В простейшей схеме применяют два резистора. При необходимости количество компонентов увеличивают для обеспечения ступенчатой регулировки. Чтобы рассчитать делитель напряжения, калькулятор онлайн использовать не обязательно. Приведенная ниже подробная инструкция поможет получить точный результат собственными силами за несколько минут.
Формула делителя напряжения
Для примера взяты определенные значения:
- Входного постоянного напряжения (Uвх) – 20 Вольт;
- Сопротивления резисторов R1 и R2 – 20 и 50 кОм, соответственно.
Уменьшение входного напряжения в два раза получится при равных значениях сопротивлений резисторов. Для настоящего примера придется рассчитать пропорцию, пользуясь формулой закона Ома:
I=Uвх/ (R1+R2)
Подставив исходные значения, несложно узнать силу тока, протекающего по данной последовательной цепи:
20/ (20 000 + 50 000) = 0,000286 А
На отдельных элементах падения напряжения составят:
- UR1 = 0,000286 * 20 000 = 5,72 V;
- UR2 = 0,000286 * 50 000 = 14,3 V.
Для непосредственного расчета напряжения на рабочем плече можно пользоваться формулой:
UR2 = Uвх * R2/ (R1+R2)
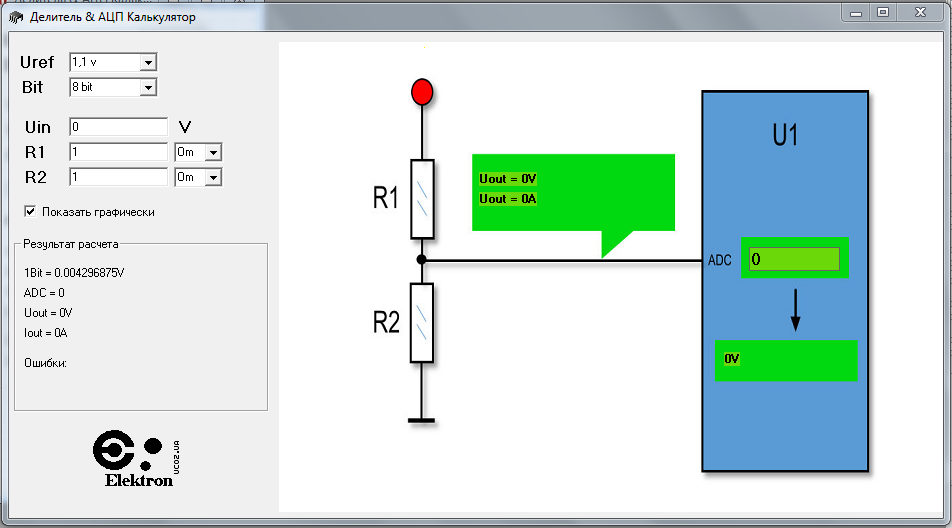
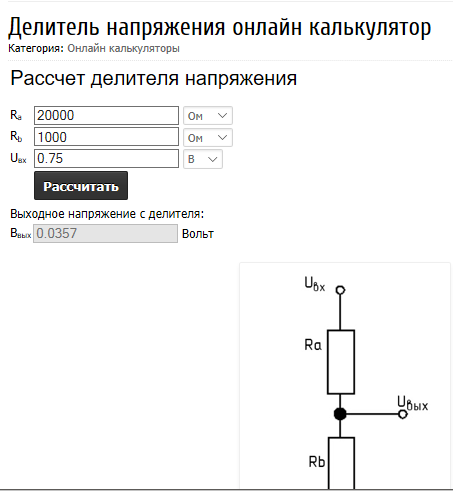
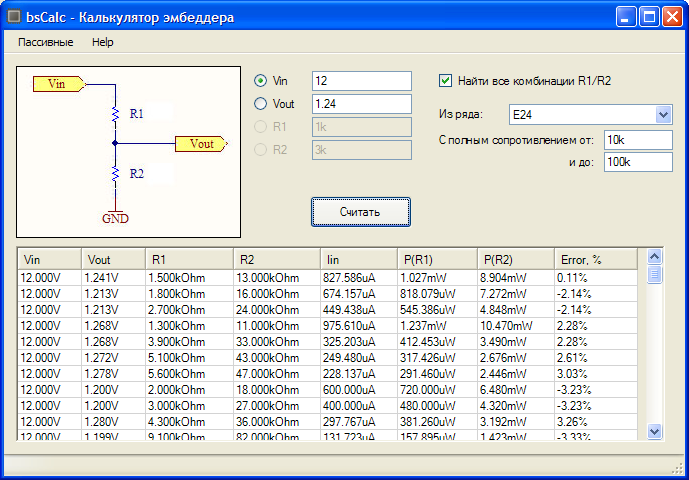
Расчет делителя напряжения калькулятором онлайн
Соответствующие программы предлагают посетителям «Паяльник» и другие специализированные сайты бесплатно и без регистрации. В стандартной форме заполняют «окошки» с напряжением на входе и выходе. После подтверждения автоматически выполняется расчет с отображением значений электрических сопротивлений резисторов и рассеиваемых мощностей.
Как понятно из примера, основные формулы не отличаются повышенной сложностью. Однако автоматизированный расчет делителя напряжения на резисторах онлайн (online) позволяет выполнять многократные теоретические эксперименты с минимальными затратами времени. Такой инструмент пригодится для точного определения основных параметров делителя.
Таблица расчетов
| Входное напряжение Uвх, V | Эл. сопротивление, Ом | Рассеиваемая мощность, Вт | Напряжение на выходе Uвых, V | ||
|---|---|---|---|---|---|
| R1 | R2 | R1 | R2 | ||
| 12 | 1000 | 2000 | 0,016 | 0,032 | 8 |
| 12 | 50000 | 4545 | 0,00242 | 0,00022 | 1 |
| 12 | 50000 | 550000 | 0,00002 | 0,00022 | 11,5 |
| 12 | 100 | 200 | 0,16 | 0,32 | 8 |
Приведенные цифры демонстрируют, что для существенного уменьшения Uвых сопротивление R1 должно быть значительно больше R2. Обратные пропорции применяют для примерного равенства напряжений на входе и выходе.
Совокупные потери в цепи определяют по рассеиваемой мощности. Чем меньше сопротивление, тем сильнее ток. Для самостоятельных расчетов пользуются формулой:
P=I2*R.
Расчёт делителя напряжения
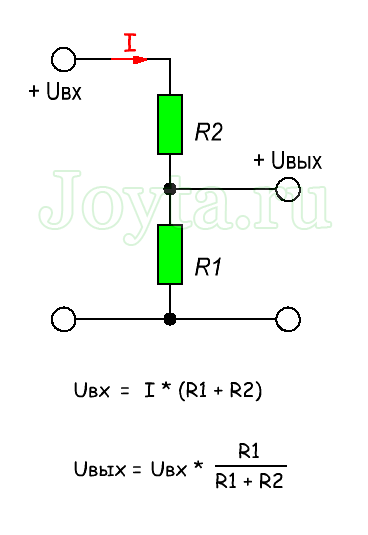
Многие сталкиваются с тем, что не существует формул для расчёта сопротивлений в делителе. На самом деле, такие формулы легко вывести. Но обо всё по порядку. Для наглядности, начнём расчёт с конца, т.е. расчитаем напряжение на выходе, зная номиналы резисторов.
Ток, протекающий через R1 и R2 одинаков, пока к среднему плечу (Uвых) ничего не подключено. Общее сопротивление резисторов при последовательном соединении равняется сумме их сопротивлений:
Rобщ = R1 + R2 = 400 + 500 = 900 Ом
По закону Ома находим силу тока, протекающего через резисторы:
I = Uвх / Rобщ = 9В / 900 Ом = 0.01 А = 10 мА
Теперь, когда нам известен ток в нижнем плече (ток, проходящий через R2), раcчитаем напряжение в нижнем плече (Опять закон Ома):
Uвых = I * R2 = 0.01А * 500 Ом = 5В
Или упрощая цепочку вычислений:
Uвых = Uвх * (R2 / (R1+R2))
Применив немного математики и прочих знаний, сдобрив всё законом Ома, можно получить следующие формулы:
R1 = (Uвх-Uвых)/Iд+Iн
R2 = Uвых / Iд
Здесь Iд и Iн — ток делителя и ток нагрузки соответственно. В общем случае, не нужно даже знать, что это за токи такие. Можно просто принять их равными Iд = 0.01 А (10 мА), а Iн = 0. То есть рассматривать делитель без нагрузки. Это приемлемо до тех пор, пока мы используем делитель только для измерений напряжения (а во всех примерах в нашей базе знаний он именно так и используется). Тогда формулы упростятся:
R1 = (Uвх-Uвых) * 100
R2 = Uвых * 100
P.S
Это совсем не важно, но обратите внимание: 100 — это не физическая величина. После принятия условия, что Iд у нас всегда равен 0.01 А, это просто коэффициент, получившийся при переносе 0.01 в числитель
Проверяем:
Входящее напряжение у нас 9 вольт, хотим получить 5 вольт на выходе. Подставляем значения в формулу, получаем:
R1 = (9-5) * 100 = 400 Ом
R2 = 5 * 100 = 500 Ом
Всё сходится!