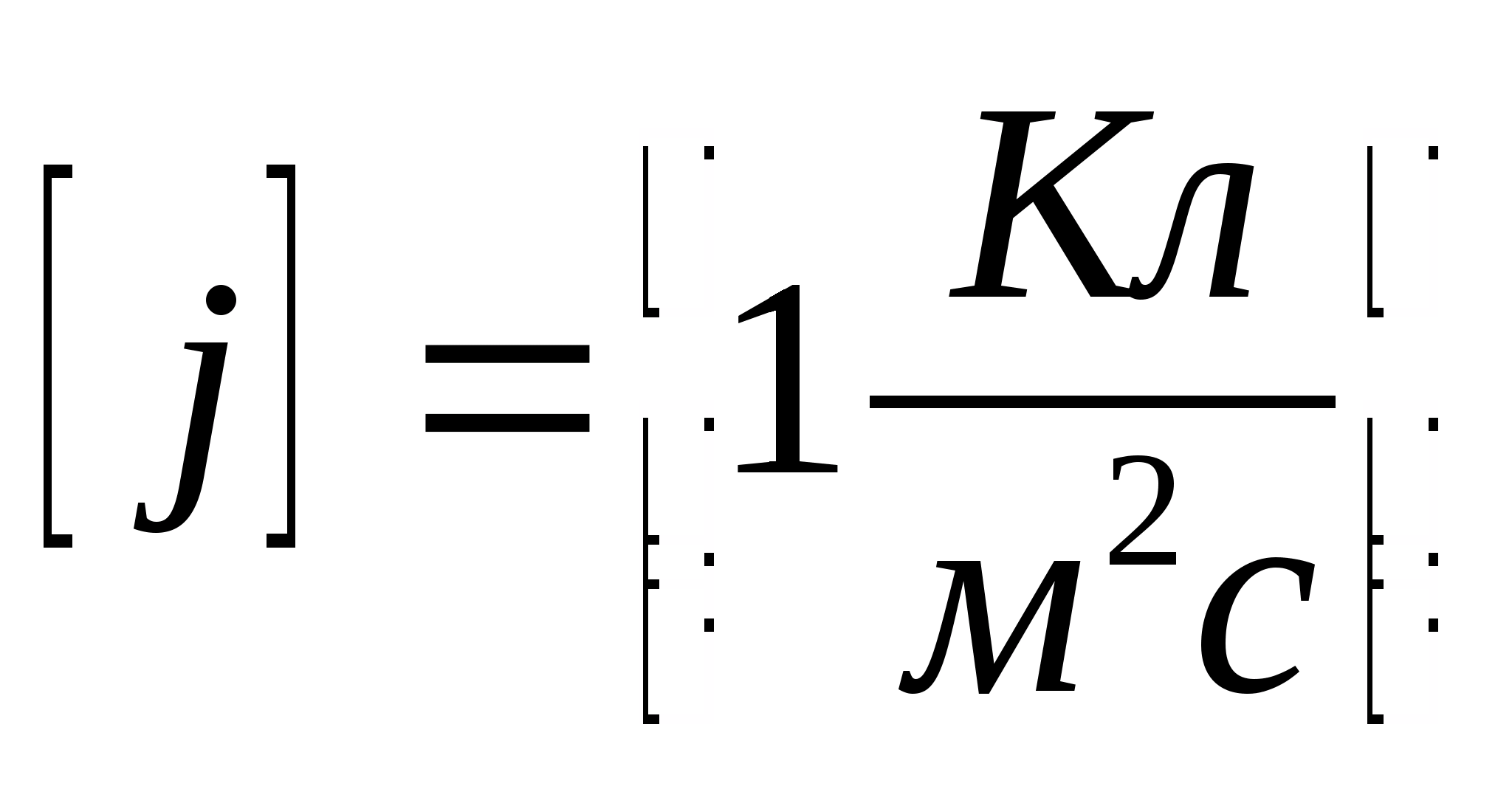Плотность тока – что это такое и в чем измеряется

Введение

Заряды, помещенные в электростатическое поле с разностью потенциалов приходят в движение. Это движение называется электрическим током, который определяется как направленное (упорядоченное) движение заряженных частиц через любое поперечное сечение проводящей среды. Величина этого тока зависит от сопротивления проводящей среды этому движению зарядов, которое, в свою очередь, зависит от поперечного сечения проводника.

Следует отметить, что в электротехнике основные физические величины, то есть единица измерения силы электрического тока ампер и единица измерения электрического заряда кулон часто бывают связаны между собой с помощью единицы длины — метра. И это неспроста. Заряд, который протекает через поперечное сечение проводящей среды, часто бывает распределен неравномерно. Поэтому вполне естественно было бы определять поток заряженных частиц через единичное поперечное сечения или единичную длину, иными словами определять плотность тока

В этой статье мы сравним электрический ток и плотность тока, а также рассмотрим важность достижения, поддержания и измерения необходимой плотности тока в различных областях электротехники и электронной техники

Введение

Заряды, помещенные в электростатическое поле с разностью потенциалов приходят в движение. Это движение называется электрическим током, который определяется как направленное (упорядоченное) движение заряженных частиц через любое поперечное сечение проводящей среды. Величина этого тока зависит от сопротивления проводящей среды этому движению зарядов, которое, в свою очередь, зависит от поперечного сечения проводника.

Следует отметить, что в электротехнике основные физические величины, то есть единица измерения силы электрического тока ампер и единица измерения электрического заряда кулон часто бывают связаны между собой с помощью единицы длины — метра. И это неспроста. Заряд, который протекает через поперечное сечение проводящей среды, часто бывает распределен неравномерно. Поэтому вполне естественно было бы определять поток заряженных частиц через единичное поперечное сечения или единичную длину, иными словами определять плотность тока

В этой статье мы сравним электрический ток и плотность тока, а также рассмотрим важность достижения, поддержания и измерения необходимой плотности тока в различных областях электротехники и электронной техники

Введение

Заряды, помещенные в электростатическое поле с разностью потенциалов приходят в движение. Это движение называется электрическим током, который определяется как направленное (упорядоченное) движение заряженных частиц через любое поперечное сечение проводящей среды. Величина этого тока зависит от сопротивления проводящей среды этому движению зарядов, которое, в свою очередь, зависит от поперечного сечения проводника.

Следует отметить, что в электротехнике основные физические величины, то есть единица измерения силы электрического тока ампер и единица измерения электрического заряда кулон часто бывают связаны между собой с помощью единицы длины — метра. И это неспроста. Заряд, который протекает через поперечное сечение проводящей среды, часто бывает распределен неравномерно. Поэтому вполне естественно было бы определять поток заряженных частиц через единичное поперечное сечения или единичную длину, иными словами определять плотность тока

В этой статье мы сравним электрический ток и плотность тока, а также рассмотрим важность достижения, поддержания и измерения необходимой плотности тока в различных областях электротехники и электронной техники

Измерение плотности тока

Гальваническая ванна, в которой наносятся покрытия металлами — как раз то место, где необходимо измерять плотность тока в жидкой проводящей среде — электролите в гальванической ванне. При этом необходимо рассчитать или измерить площадь поверхности покрываемой металлом детали, а также измерить ток, протекающий в ванне от анода к детали. Выпускаются приборы, позволяющие непосредственно измерить плотность тока в любой точке ванны. Они позволяют работникам гальванического цеха точно измерить как идет процесс покрытия металлом в каждой точки изделия. Измеритель плотности тока электролита чаще всего состоит из датчика с маленькой тороидальной катушкой и измерительного блока с дисплеем, который измеряет ток, индуцированный в катушке током в электролите внутри нее. Процессор таких приборов определяет значение плотности тока в точке измерения исходя из измеренного тока и площади катушки и выводит его на дисплей прямо в А/фут² или A/дм².

Еще одним примером измерения плотности тока являются солнечные батареи. Обычно плотности токов короткого замыкания распределены неравномерно по поверхности фотоэлементов. Различия в плотностях тока могут быть обусловлены различными сроками существования носителей в фотоэлементе, различными расстояниями до выводов и другими факторами. Исследователям интересно получить карту распределения плотностей токов по всей площади фотоэлемента. Для измерения плотности тока фотоэлемент освещают очень узким потоком электронов или лучом света, который сканирует поверхность фотоэлемента. При этом регистрируется возникающий фототок. Таким образом создается карта плотностей тока, которую в дальнейшем можно использовать для оптимизации устройства.

Автор статьи: Анатолий Золотков

Закон Ома

В линейной и изотропной проводящей среде плотность тока связана с напряжённостью электрического поля в данной точке по закону Ома:

j→=σE→{\displaystyle {\vec {j}}=\sigma {\vec {E}}}

где σ {\displaystyle \sigma \ } — удельная проводимость среды, E→{\displaystyle {\vec {E}}} — напряжённость электрического поля. Или:

j→=1ρE→,{\displaystyle {\vec {j}}={\frac {1}{\rho }}{\vec {E}},}

где ρ {\displaystyle \rho \ } — удельное сопротивление.

В линейной анизотропной среде имеет место такое же соотношение, однако удельная электропроводность σ{\displaystyle \sigma } в этом случае, вообще говоря, должна рассматриваться как тензор, а умножение на неё — как умножение вектора на матрицу.

Формула для работы электрического поля (плотности её мощности)

w=E→⋅j→,{\displaystyle w={\vec {E}}\cdot {\vec {j}},}

вместе с законом Ома принимает для изотропной электропроводности вид:

w=σE2=j2σ≡ρj2,{\displaystyle w=\sigma E^{2}={\frac {j^{2}}{\sigma }}\equiv \rho j^{2},}

где σ{\displaystyle \sigma } и ρ{\displaystyle \rho } — скаляры, а для анизотропной:

w=E→σE→=j→ρj→,{\displaystyle w={\vec {E}}\sigma {\vec {E}}={\vec {j}}\rho {\vec {j}},}

где подразумевается матричное умножение (справа налево) вектора-столбца на матрицу и на вектор-строку, а тензор σ{\displaystyle \sigma } и тензор ρ{\displaystyle \rho } порождают соответствующие квадратичные формы.

Формула вычисления

Рассматриваемая величина находится в обратной зависимости от размеров сечения (чем больше площадь, тем меньше плотность тока) и временного периода прохождения электрозаряда и в прямой – от величины этого заряда.

Это можно записать так:

j=Δq/ΔtΔS (q тут – элементарно малый заряд, t – бесконечно малый промежуток времени, а S – площадь сечения).

Так как токовая сила выражается как частное заряда и временного промежутка его прохода, формулу можно записать и так:

j= I/ΔS.

Формула плотности тока с опорой на параметры перемещающихся зарядов будет выглядеть так:

j=q*n*V (V тут – скорость, а n – концентрация электронных частиц).

Определения

Электрический ток

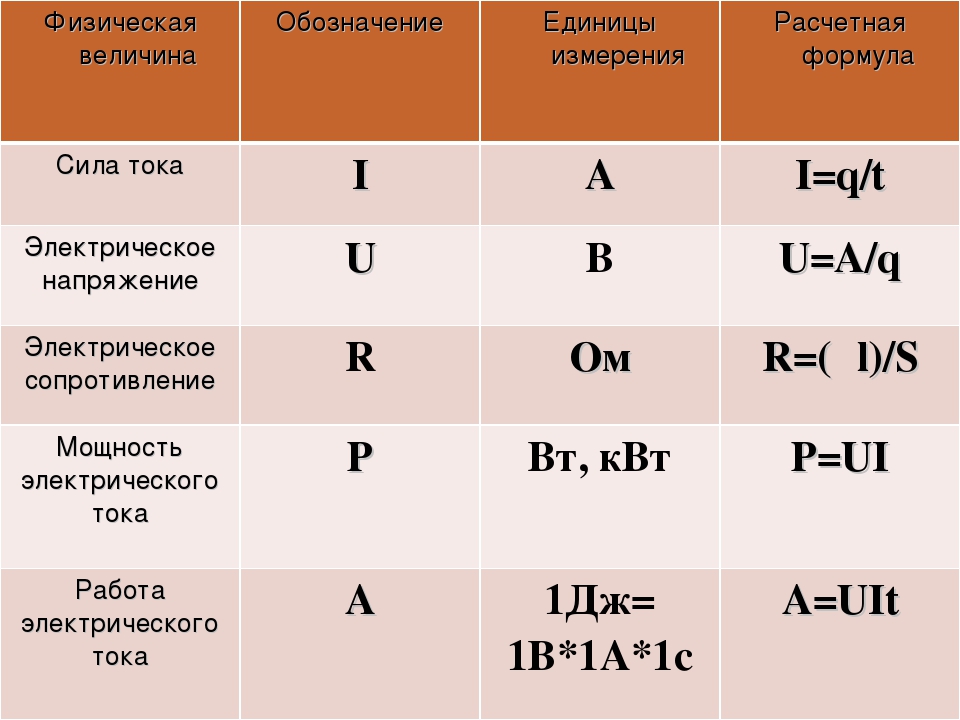
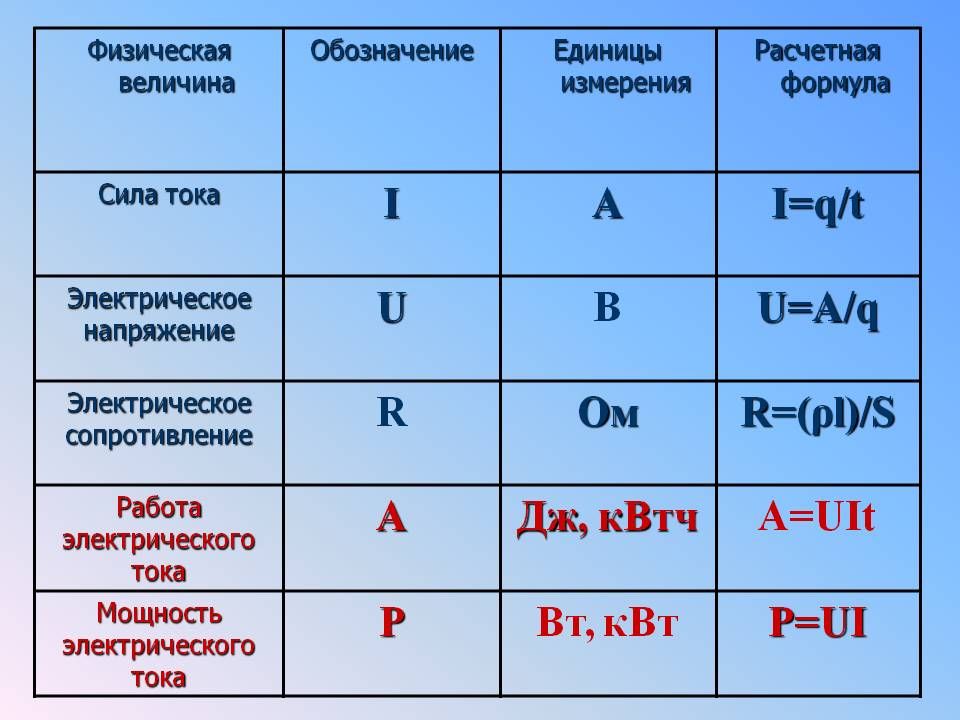
Электрический ток I определяется как направленное движение электрических зарядов вдоль линии (например, тонкого провода), по поверхности (например, по листу проводящего материала) или в объеме (например, в электронной или газоразрядной лампе). В СИ единицей измерения электрического тока является ампер, определяемый как поток электрических зарядов через поперечное сечение проводника со скоростью один кулон в секунду.

Объемная плотность тока

Плотность тока (называемая также объемной плотностью тока) представляет собой векторное поле в трехмерном проводящем пространстве. В каждой точке такого пространства плотность тока представляет собой полный поток электрических зарядов в единицу времени, проходящий через единичное поперечное сечение. Обозначается объемная плотность векторным символом J. Если мы рассмотрим обычный случай проводника с током, то ток в амперах делится на поперечное сечение проводника. В СИ объемная плотность тока измеряется в амперах на квадратный метр (А/м²).

Например, если по мощной шине электрической подстанции с поперечным сечением 3 х 33,3 мм = 100 мм² = 0,0001 м² течет ток 50 ампер, то плотность тока в таком проводнике будет составлять 500 000 А/м².

Линейная плотность тока

Иногда в электронных устройствах ток течет через очень тонкую пленку металла или тонкий слой металла, имеющий переменную толщину. В таких случаях исследователей и конструкторов интересуют только ширина, а не общее поперечное сечение таких очень тонких проводников. В этом случае они измеряют линейную плотность тока — векторная величину, равную пределу произведения плотности тока проводимости, протекающего в тонком слое у поверхности тела, на толщину этого слоя, когда последняя стремится к нулю (это определение по ГОСТ 19880-74). В Международной системе единиц (СИ) линейная плотность тока измеряется в амперах на метр и в системе СГС в эрстедах. 1 эрстед равен напряжённости магнитного поля в вакууме при индукции 1 гаусс. Иначе линейную плотность тока определяют как ток, приходящийся на единицу длины в направлении, перпендикулярном току.

Например, если ток величиной 100 мА течет в тонком проводнике шириной 1 мм, то линейная плотность тока равна 0,0001 A : 0,001 m = 10 ампер на метр (А/м). Линейная плотность тока обозначается векторным символом А.

Поверхностная плотность тока

Линейная плотность тока тесно связана с понятием поверхностной плотности тока , которая определяется как сила электрического тока, протекающего через поперечное сечение проводящей среды единичной площади и обозначается векторным символом K. Как и линейная плотность тока, поверхностная плотность тока также является векторной величиной, модуль которой представляет собой электрический ток через поперечное сечение проводящей среды в данном месте, а направление перпендикулярно к площади поперечного сечения проводника. Такой проводящей средой может быть, например, проводник с током, электролит или ионизированный газ. В системе СИ плотность тока измеряется в амперах на квадратный метр.

Вектор или скаляр?

Отметим, что в отличие от векторной плотности тока, сам ток является скалярной величиной. Это можно объяснить тем фактом, что ток определяется как количество зарядов, перемещающихся в единицу времени; поэтому было бы нецелесообразно добавлять направление к величине, представляющей количество в единицу времени. В то же время, плотность тока рассматривается в объеме с множеством поперечных сечений, через которые проходит ток, поэтому имеет смысл определять плотность тока как вектор или как векторное пространство. Можно также отметить, что плотность тока является вектором в связи с тем, что это произведение плотности заряда на скорость его перемещения в любом месте пространства.

Сила тока и плотность

Для того чтобы понять, как работает та или иная электрическая величина, необходимо знать условия и степень их взаимодействия между собой. Большое значение имеет зависимость силы и плотности тока в проводнике. Перед тем как рассматривать эту зависимость следует более подробно остановиться на понятии электрического тока.

Под действием определенных факторов в металлах, выступающих в роли основных проводников, образуется направленное движение заряженных частиц. Как правило, это электроны, обладающие отрицательным зарядом. Существуют и другие проводники, называемые электролитами, в которых направленное движение создается ионами, которые могут быть положительными или отрицательными. Третий вид проводников представляет собой различные газы, где электрический ток создается не только электронами, но и с помощью положительных и отрицательных ионов. Величину плотности тока можно определить в любом проводнике, но более наглядно это будет на примере металлов.

Условно электрический ток имеет направление, совпадающее с направлением движения положительно заряженных частиц. Для его создания и существования необходимо соблюдение двух основных условий. В первую очередь, это сами заряженные частицы, которые могут свободно перемещаться в проводнике под действием сил электрического поля. Соответственно, необходимо само электрическое поле, способное существовать в проводнике в течение длительного времени под действием источника тока.

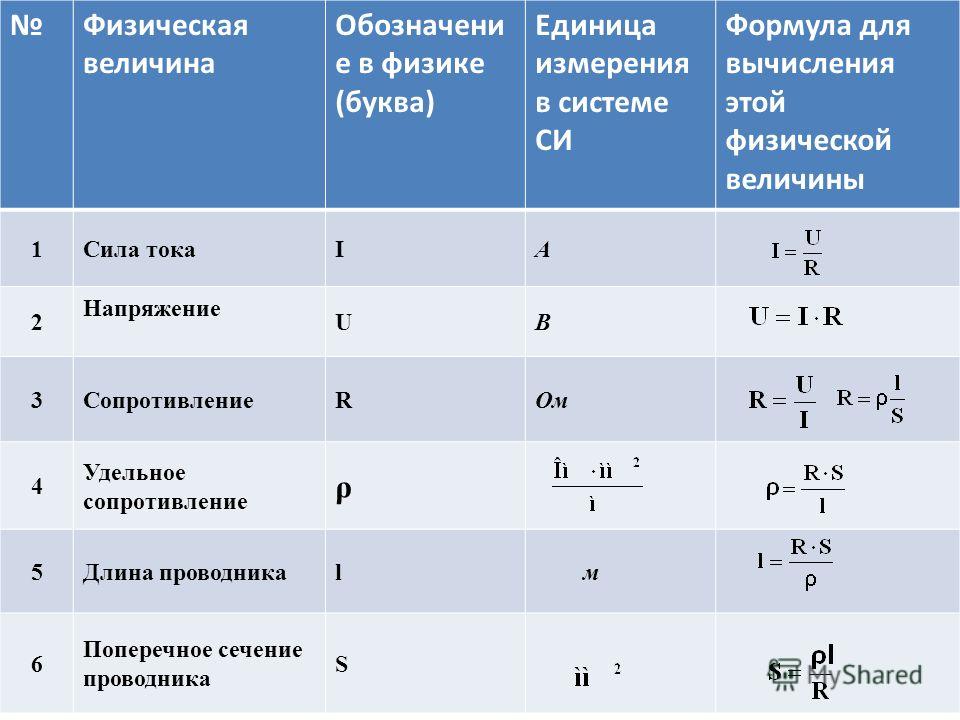
Сила (I) и плотность (j) электрического тока являются его основными характеристиками. Сила тока считается скалярной физической величиной, определяемой как отношение заряда ∆q, проходящего через поперечное сечение проводника в течение некоторого времени ∆t, к данному временному промежутку. В виде формулы это будет выглядеть следующим образом: I = ∆q/∆t. Единицей измерения силы тока служит ампер. Это позволит в дальнейшем решить вопрос, как найти плотность тока.

Существует связь силы тока со скоростью свободных зарядов, находящихся в упорядоченном движении. Определить эту зависимость можно на примере участка проводника, имеющего площадь сечения S и длину ∆l. Заряд каждой частицы принимается за q0, а объем проводника ограничивается сечениями № 1 и № 2. В этом объеме количество частиц составляет nS∆l, где n является концентрацией частиц. Величина их общего заряда составляет: ∆q = q0nS∆l. Упорядоченное движение свободных зарядов осуществляется со средней скоростью hvi. Следовательно за установленный промежуток времени ∆t = ∆I/ hvi все частицы, находящиеся в этом объеме, пройдут через сечение № 2. В результате, сила тока составит I = ∆q/∆t, как уже и было отмечено.

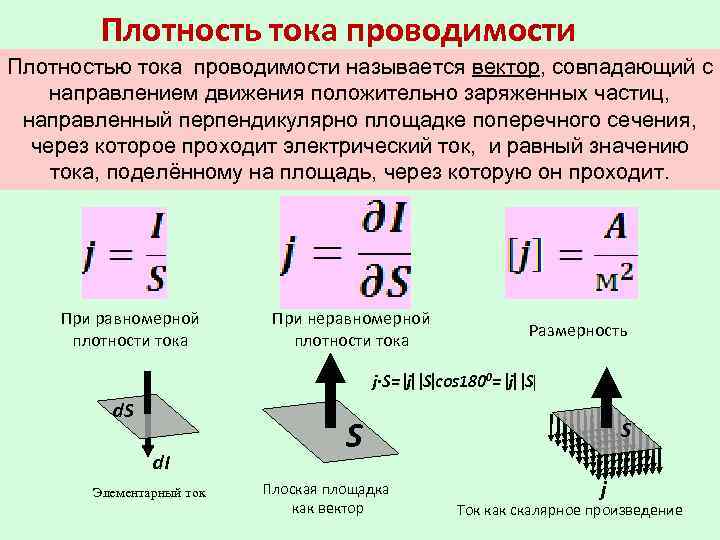
Сила тока имеет непосредственную связь с плотностью тока j представляющей собой векторную физическую величину. Ее модуль определяется как отношение силы тока I и площади поперечного сечения проводника. Плотность формула отражает как j = I/S. Вектор плотности тока совпадает с вектором скорости упорядоченно движущихся положительно заряженных частиц. Постоянный ток обладает плотностью, имеющей стабильное значение на всем поперечном сечении проводника. Таким образом, плотность и сила тока самым тесным образом связаны между собой.

Определения

Электрический ток

Электрический ток I определяется как направленное движение электрических зарядов вдоль линии (например, тонкого провода), по поверхности (например, по листу проводящего материала) или в объеме (например, в электронной или газоразрядной лампе). В СИ единицей измерения электрического тока является ампер, определяемый как поток электрических зарядов через поперечное сечение проводника со скоростью один кулон в секунду.

Объемная плотность тока

Плотность тока (называемая также объемной плотностью тока) представляет собой векторное поле в трехмерном проводящем пространстве. В каждой точке такого пространства плотность тока представляет собой полный поток электрических зарядов в единицу времени, проходящий через единичное поперечное сечение. Обозначается объемная плотность векторным символом J. Если мы рассмотрим обычный случай проводника с током, то ток в амперах делится на поперечное сечение проводника. В СИ объемная плотность тока измеряется в амперах на квадратный метр (А/м²).

Например, если по мощной шине электрической подстанции с поперечным сечением 3 х 33,3 мм = 100 мм² = 0,0001 м² течет ток 50 ампер, то плотность тока в таком проводнике будет составлять 500 000 А/м².

Линейная плотность тока

Иногда в электронных устройствах ток течет через очень тонкую пленку металла или тонкий слой металла, имеющий переменную толщину. В таких случаях исследователей и конструкторов интересуют только ширина, а не общее поперечное сечение таких очень тонких проводников. В этом случае они измеряют линейную плотность тока — векторная величину, равную пределу произведения плотности тока проводимости, протекающего в тонком слое у поверхности тела, на толщину этого слоя, когда последняя стремится к нулю (это определение по ГОСТ 19880-74). В Международной системе единиц (СИ) линейная плотность тока измеряется в амперах на метр и в системе СГС в эрстедах. 1 эрстед равен напряжённости магнитного поля в вакууме при индукции 1 гаусс. Иначе линейную плотность тока определяют как ток, приходящийся на единицу длины в направлении, перпендикулярном току.

Например, если ток величиной 100 мА течет в тонком проводнике шириной 1 мм, то линейная плотность тока равна 0,0001 A : 0,001 m = 10 ампер на метр (А/м). Линейная плотность тока обозначается векторным символом А.

Поверхностная плотность тока

Линейная плотность тока тесно связана с понятием поверхностной плотности тока , которая определяется как сила электрического тока, протекающего через поперечное сечение проводящей среды единичной площади и обозначается векторным символом K. Как и линейная плотность тока, поверхностная плотность тока также является векторной величиной, модуль которой представляет собой электрический ток через поперечное сечение проводящей среды в данном месте, а направление перпендикулярно к площади поперечного сечения проводника. Такой проводящей средой может быть, например, проводник с током, электролит или ионизированный газ. В системе СИ плотность тока измеряется в амперах на квадратный метр.

Вектор или скаляр?

Отметим, что в отличие от векторной плотности тока, сам ток является скалярной величиной. Это можно объяснить тем фактом, что ток определяется как количество зарядов, перемещающихся в единицу времени; поэтому было бы нецелесообразно добавлять направление к величине, представляющей количество в единицу времени. В то же время, плотность тока рассматривается в объеме с множеством поперечных сечений, через которые проходит ток, поэтому имеет смысл определять плотность тока как вектор или как векторное пространство. Можно также отметить, что плотность тока является вектором в связи с тем, что это произведение плотности заряда на скорость его перемещения в любом месте пространства.

Объемная плотность магнитной энергии

Формула нахождения объемной плотности энергии имеет такой вид:

ω=W/V.

Под ω здесь подразумевается собственно искомая плотность, под W – энергия имеющегося поля, под V – объем пространства, в котором поле проявляет активность. Если выразить значение W через магнитную проницаемость µ и индукцию В и подставить в формулу, она приобретет следующий вид:

ω=В2/2* µ0* µ (здесь µ0 – это магнитная постоянная).

Преобразование с использованием вектора индукции применяется, чтобы исключить привязку активного магнитного поля к особенностям дросселя. Формула для вычисления индукционной характеристики выглядит так:

B= µ0* µ*I*n.

I здесь – токовая сила в катушечной цепочке, через n выражается такая величина, как плотность обмотки. Она равна частному количества витков в соленоидной обмотке и длины фрагмента, на котором размещены витки. Тогда формула для W

W= В2*V/2* µ0* µ.

Подставив выражение в основную формулу плотности, можно привести его к ранее обозначенному виду.

1.3.27

Увеличение количества линий или цепей сверх
необходимого по условиям надежности электроснабжения в целях удовлетворения
экономической плотности тока производится на основе технико-экономического
расчета. При этом во избежание увеличения количество линий или цепей
допускается двукратное превышение нормированных значений, приведенных в табл.
1.3.36.

Таблица 1.3.36. Экономическая плотность тока

В технико-экономических расчетах следует учитывать все вложения в дополнительную линию, включая оборудование и камеры распределительных устройств на обоих концах линий. Следует также проверять целесообразность повышения напряжения линии.

Данными указаниями следует руководствоваться также при
замене существующих проводов проводами большего сечения или при прокладке
дополнительных линий для обеспечения экономической плотности тока при росте
нагрузки. В этих случаях должна учитываться также полная стоимость всех работ
по демонтажу и монтажу оборудования линии, включая стоимость аппаратов и
материалов.

Закон Ома

Сопротивление тока: формула

Для токопроводящей среды, обладающей изотропными характеристиками, данный закон имеет следующий вид:

j=E* σ,

где j – плотность идущего электротока, Е – полевая напряженность в рассматриваемой точке (скалярная величина, как и предыдущая), а σ – удельная проводимость средового окружения.

Что касается работы электрополя для такой среды (w), то она может быть выражена следующими формулами:

w= E2* σ=j2/σ=p*j2 (p здесь – удельное сопротивление).

Выражение для работы в этом случае примет вид:

w=E* σ *E=j*p*j (E и j в данном случае – скалярные величины).

В матрице справа налево умножают столбчатый вектор на строчной и на матрицу. Тензорные величины р и σ генерируют релевантные им квадратичные формы.

Закон Ома

В линейной и изотропной проводящей среде плотность тока связана с напряжённостью электрического поля в данной точке по закону Ома:

j→=σE→{\displaystyle {\vec {j}}=\sigma {\vec {E}}}

где σ {\displaystyle \sigma \ } — удельная проводимость среды, E→{\displaystyle {\vec {E}}} — напряжённость электрического поля. Или:

j→=1ρE→,{\displaystyle {\vec {j}}={\frac {1}{\rho }}{\vec {E}},}

где ρ {\displaystyle \rho \ } — удельное сопротивление.

В линейной анизотропной среде имеет место такое же соотношение, однако удельная электропроводность σ{\displaystyle \sigma } в этом случае, вообще говоря, должна рассматриваться как тензор, а умножение на неё — как умножение вектора на матрицу.

Формула для работы электрического поля (плотности её мощности)

w=E→⋅j→,{\displaystyle w={\vec {E}}\cdot {\vec {j}},}

вместе с законом Ома принимает для изотропной электропроводности вид:

w=σE2=j2σ≡ρj2,{\displaystyle w=\sigma E^{2}={\frac {j^{2}}{\sigma }}\equiv \rho j^{2},}

где σ{\displaystyle \sigma } и ρ{\displaystyle \rho } — скаляры, а для анизотропной:

w=E→σE→=j→ρj→,{\displaystyle w={\vec {E}}\sigma {\vec {E}}={\vec {j}}\rho {\vec {j}},}

где подразумевается матричное умножение (справа налево) вектора-столбца на матрицу и на вектор-строку, а тензор σ{\displaystyle \sigma } и тензор ρ{\displaystyle \rho } порождают соответствующие квадратичные формы.

Допустимая плотность тока для медного провода

При создании сетей в современных объектах недвижимости предпочитают использовать именно такие проводники. При одинаковом сечении они меньше перегреваются, по сравнению с алюминиевыми аналогами. В многожильном исполнении медные кабели хорошо подходят для создания сетевых соединительных шнуров, удлинителей. Их можно использовать для создания поворотов с малым радиусом.

Тепловой нагрев

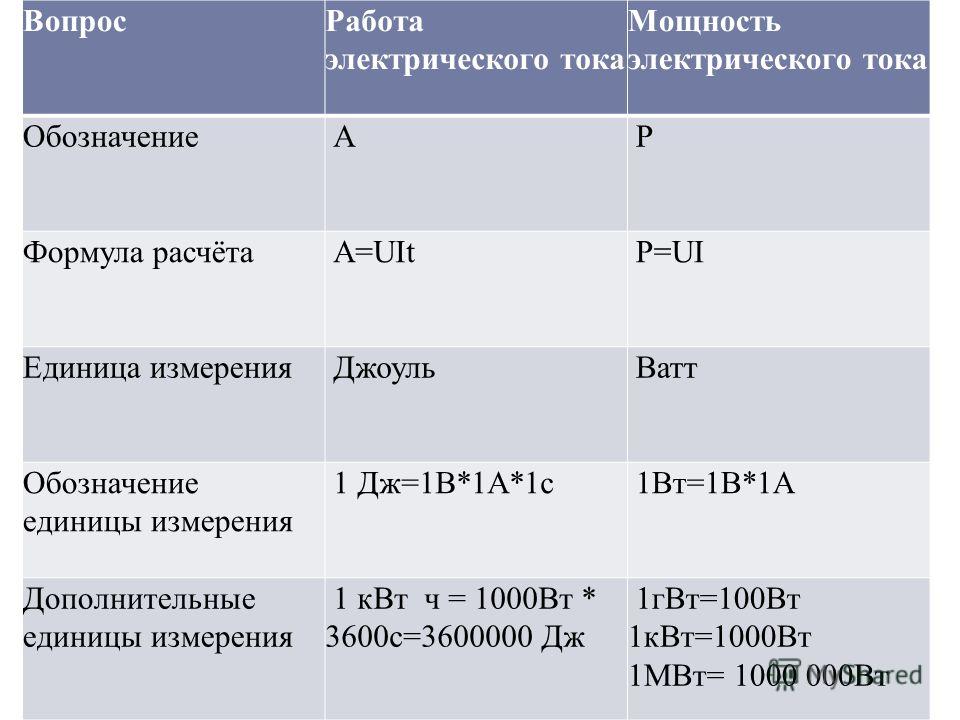
Для расчета количества тепла (Q), выделяемого проводником, пользуются формулой I*2*R*t, где:

• I – сила тока, в амперах;
• R – сопротивление одного метра медного проводника;
• t – время испытания в определенных условиях.

Рассеивание тепла при работе кабеля

Тонкие проводники эффективно отдают тепловую энергию окружающей среде. На процесс оказывают существенное влияние конкретные условия. Как отмечено выше, контакт оболочки с водой существенно улучшает охлаждение.

По мере увеличения сечения часть энергии расходуется для нагрева прилегающих слоев. Этим объясняется постепенное снижение допустимой плотности тока в расчете на единицу площади.

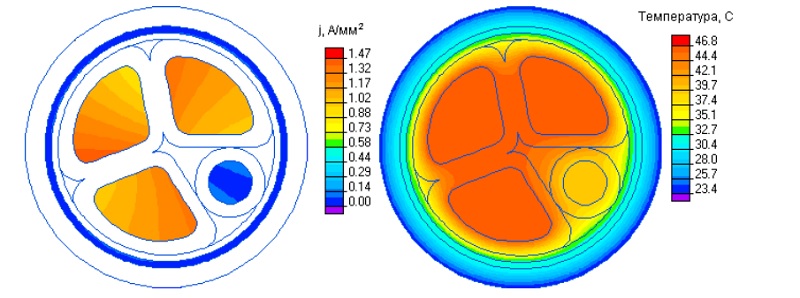Распределение температур в кабельной продукции

На рисунке хорошо видно, как при уменьшении изоляционного слоя улучшается теплоотдача.

Падение напряжения

Этот параметр несложно рассчитать по закону Ома (U=R*I) с учетом электрического сопротивления соответствующего материала. Удельное значение для меди берут 0,0175 Ом *мм кв./ метр. С помощью формул вычисляют на участке определенной длины падение напряжения. При сечении 1,5 мм кв. на каждый метр потери составят 0,01117 Вольт.

Допустимая плотность тока

Этот относительный параметр показывает разрешенный нормативами ток на один мм кв. площади сечения. Отмеченные выше тенденции по изменению теплоотдачи при увеличении размеров проводника подтверждаются расчетами и данными лабораторных испытаний.

Таблица допустимых значений плотности тока для разных условий в медном проводнике

Поперечное сечение, мм кв.	Ток (А)/ Плотность тока (А/ мм кв.)
	Для трассы в здании	Монтаж на открытом воздухе
6	73/ 12,2	76/ 12,6
10	103/ 10,3	108/ 10,8
25	165/ 6,6	205/ 8,2
50	265/ 5,3	335/ 6,7

Пути повышения допустимого тока

Существенное значение имеют действительные условия эксплуатации трассы электроснабжения, трансформаторов, установок. Снизить рассматриваемые нагрузки можно с помощью хорошей вентиляции, естественной или принудительной. Хороший отвод тепла получится с применением перфорированных металлических коробов, которые не затрудняют прохождение конвекционных потоков и одновременно выполняют функции радиатора.

В некоторых ситуациях пригодится квалифицированно составленный временной график. Стиральная машина при нагреве воды и в режиме сушки потребляет много электроэнергии. Ее можно настроить на автоматическое выполнение рабочих операций в ночные часы. Если снабжающие организации предлагают соответствующую тарификацию, получится дополнительная экономия денежных средств.

Вентилятор обеспечивает эффективное охлаждение проводников, которые установлены в микроволновой печи

Допустимый ток и сечение проводов

Лучшие показатели теплообмена при остальных равных условиях характерны для проводников с относительно меньшей площадью поперечного сечения.

Таблица токовых параметров для кабелей с медными жилами

Сечение, мм кв.	Плотность тока, А/ мм кв.	Ток, А
1	15	15
1,5	13,3	20
2,5	10,8	27
16	5,7	92
25	4,9	123

Измерение плотности тока

Гальваническая ванна, в которой наносятся покрытия металлами — как раз то место, где необходимо измерять плотность тока в жидкой проводящей среде — электролите в гальванической ванне. При этом необходимо рассчитать или измерить площадь поверхности покрываемой металлом детали, а также измерить ток, протекающий в ванне от анода к детали. Выпускаются приборы, позволяющие непосредственно измерить плотность тока в любой точке ванны. Они позволяют работникам гальванического цеха точно измерить как идет процесс покрытия металлом в каждой точки изделия. Измеритель плотности тока электролита чаще всего состоит из датчика с маленькой тороидальной катушкой и измерительного блока с дисплеем, который измеряет ток, индуцированный в катушке током в электролите внутри нее. Процессор таких приборов определяет значение плотности тока в точке измерения исходя из измеренного тока и площади катушки и выводит его на дисплей прямо в А/фут² или A/дм².

Еще одним примером измерения плотности тока являются солнечные батареи. Обычно плотности токов короткого замыкания распределены неравномерно по поверхности фотоэлементов. Различия в плотностях тока могут быть обусловлены различными сроками существования носителей в фотоэлементе, различными расстояниями до выводов и другими факторами. Исследователям интересно получить карту распределения плотностей токов по всей площади фотоэлемента. Для измерения плотности тока фотоэлемент освещают очень узким потоком электронов или лучом света, который сканирует поверхность фотоэлемента. При этом регистрируется возникающий фототок. Таким образом создается карта плотностей тока, которую в дальнейшем можно использовать для оптимизации устройства.

Автор статьи: Анатолий Золотков

Меры безопасности

Главным правилом безопасности во время работы с токами станет то, что перед любыми действиями требуется обесточить электросеть. В процессе работ также необходимо следовать таким рекомендациям:

• Запрещено ремонтировать включенное в электросеть приспособление.
• При осуществлении работ на электрощитке должно присутствовать предупреждение.
• Работа с высоким напряжением допустимо лишь с помощником.
• Требуется наблюдать за изоляцией каждого провода и контролировать заземление.

Напряжение свыше 24 вольт будет опасно для жизни. Во время работы с напряжением больше данного параметра требуется спецдопуск. При работах необходимо пользоваться специнструментами с повышенным уровнем защиты.

Правила безопасности

Использование электротока разнообразно, так как без него нельзя представить сегодня жизнь. Необходимо понять принципы его функционирования для направления электроэнергии в правильное русло. Электроток течет по законам физики, используемым для создания разнообразных приспособлений. Чтобы грамотно использовать его, требуется ознакомиться с основными электровеличинами.

Формула вычисления

Рассматриваемая величина находится в обратной зависимости от размеров сечения (чем больше площадь, тем меньше плотность тока) и временного периода прохождения электрозаряда и в прямой – от величины этого заряда.

Это можно записать так:

j=Δq/ΔtΔS (q тут – элементарно малый заряд, t – бесконечно малый промежуток времени, а S – площадь сечения).

Так как токовая сила выражается как частное заряда и временного промежутка его прохода, формулу можно записать и так:

j= I/ΔS.

Формула плотности тока с опорой на параметры перемещающихся зарядов будет выглядеть так:

j=q*n*V (V тут – скорость, а n – концентрация электронных частиц).

Измерение плотности энергии магнитных полей

Свободная энергия эфира: генераторы свободной энергии

Данная величина показывает энергию, содержащуюся в единице объема окружающей среды, подпадающей под влияние поля. Обозначается она греческой буквой ω. Для вычисления применяется формула:

ω=W/V, в данном случае W – это полевая энергия в объеме пространства V.

Единица измерения плотности поля в международной системе СИ тоже выглядит как частное единиц, в которых измеряются эти величины: джоулей и кубических метров (Дж/м3). Показатель для аккумуляторов (ионных, свинцово-кислотных и других) указывают в прилагающейся документации.

Для соленоида, подсоединенного в электрическую цепь, оба составляющих этого частного можно выразить через следующие единицы:

1. Значение энергетического ресурса поля будет равным уполовиненному произведению индуктивности соленоида на квадрат токовой силы в его обмотке:

W=L*I2/2.

1. В качестве «пространства» рассматривается сама катушка, тогда V=S*l, где S – площадь сечения катушечного элемента в поперечнике, а l – его длина.

Тогда конечная формула принимает следующий облик:

ω=L*I2/2*S*l.